
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифракционная решетка как спектральный приборСодержание книги
Поиск на нашем сайте
Угловая дисперсия Одной из главных характеристик спектрального прибора является угловая дисперсия. По определению, угловой дисперсией
Здесь и далее В определении угловой дисперсии
Угловая дисперсия принимает только положительные значения. Угловая дисперсия тем больше, чем меньше период решетки, она растет с ростом порядка максимума. Угловая дисперсия одинакова в максимумах с порядками
Рис. 13. К определению угловой дисперсии Разрешающая сила дифракционной решетки Разрешающая сила дифракционной решетки определяется следующим образом:
Здесь Критерий Релея Критерий Релея определяет величину
По определению разрешающая сила:
Рис. 14.Критерий Релея Разрешающая сила R есть величина, обратная относительной погрешности определения длины волны. Она показывает, во сколько раз длина волны Подчеркнем, что
Рис.15. Поперечные размеры пучка и решетки Если же Кроме того, предполагается, что колебания от всех Дифракция на пространственной решетке. Формула Вульфа — Брэггов Для наблюдения дифракционной картины необходимо, чтобы постоянная решетки была того же порядка, что и длина волны падающего излучения. Кристаллы, являясь трехмерными пространственными решетками, имеют постоянную порядка 10-10м и, следовательно, непригодны для наблюдения дифракции в видимом свете (~=5·10-7м). Эти факты позволили немецкому физику М. Лауэ (1879—1960 гг.) прийти к выводу, что в качестве естественных дифракционных решеток для рентгеновского излучения можно использовать кристаллы, поскольку расстояние между атомами в кристаллах одного порядка с рентгеновского излучения (10-12―10-8м). Простой метод расчета дифракции рентгеновского излучения от кристаллической решетки предложен независимо друг от друга советским физиком Г. В. Вульфом (1863—1925 гг.) и английскими физиками Г. и Л. Брэггами (отец (1862—1942гг.) и сын (1890—1971гг.)). Они предположили, что дифракция рентгеновских лучей является результатом их отражения от системы параллельных кристаллографических плоскостей (плоскостей, в которых лежат узлы (атомы) кристаллической решетки). Представим кристаллы в виде совокупности параллельных кристаллографических плоскостей (рис. 27), отстоящих друг от друга на расстоянии
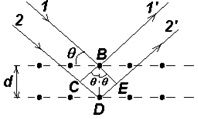
Рис.16. Дифракция рентгеновских лучей Пучок параллельных монохроматических рентгеновских лучей (1, 2) падает под углом скольжения (угол между направлением падающих лучей и кристаллографической плоскостью) и возбуждает атомы кристаллической решетки, которые становятся источниками когерентных вторичных волн 1'и 2', интерферирующих между собой, подобно вторичным волнам, от щелей дифракционной решетки. Максимумы интенсивности (дифракционные максимумы) наблюдаются в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе. Эти направления удовлетворяют формуле Вульфа – Брэггов:
т. е. при разности хода между двумя лучами, отраженными от соседних кристаллографических плоскостей, кратной целому числу длин волн, наблюдается дифракционный максимум. При произвольном направлении падения монохроматического рентгеновского излучения на кристалл дифракция не возникает. Чтобы ее наблюдать, надо, поворачивая кристалл, найти угол скольжения. Дифракционная картина может быть получена и при произвольном положении кристалла, для чего нужно пользоваться непрерывным рентгеновским спектром, испускаемым рентгеновской трубкой. Тогда для таких условий опыта всегда найдутся длины волн, удовлетворяющие условию (32).
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.163.120 (0.006 с.) |

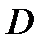 называется величина:
называется величина: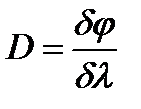 (22)
(22)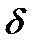 – знак дифференциала, так как буква
– знак дифференциала, так как буква 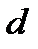 используется – она обозначает постоянную решетки.
используется – она обозначает постоянную решетки.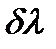 – разность длин волн двух соседних линий,
– разность длин волн двух соседних линий, 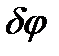 – соответствующая разность углов, под которыми наблюдаются главные максимумы. Выразим угловую дисперсию через постоянную решетки
– соответствующая разность углов, под которыми наблюдаются главные максимумы. Выразим угловую дисперсию через постоянную решетки 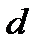 , порядок спектра
, порядок спектра 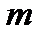 и угол
и угол 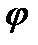 , под которым наблюдается максимум. Для этого найдем дифференциал от правой и левой части условия главного максимума:
, под которым наблюдается максимум. Для этого найдем дифференциал от правой и левой части условия главного максимума: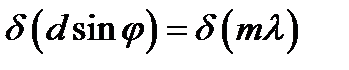 , (23)
, (23)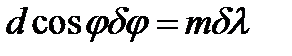 , (24)
, (24)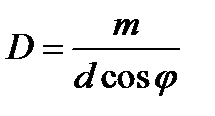 (25)
(25)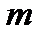 и
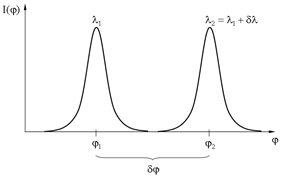
и 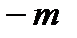 . При малых
. При малых 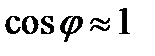 и
и 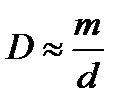 .
.
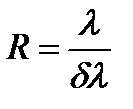 (26)
(26)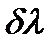 – минимальная разница в длинах волн соседних спектральных линий, при которой эти линии еще можно наблюдать раздельно.
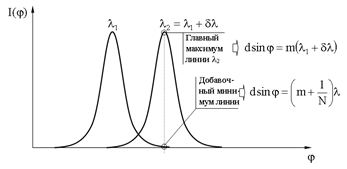
– минимальная разница в длинах волн соседних спектральных линий, при которой эти линии еще можно наблюдать раздельно.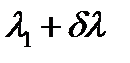 и добавочный минимум линии
и добавочный минимум линии 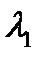 совпадает, следовательно:
совпадает, следовательно: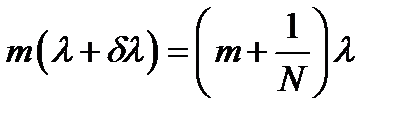 (27)
(27)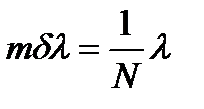 (28)
(28)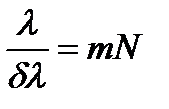 (29)
(29)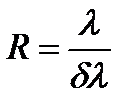 (30)
(30) В результате получим:
В результате получим: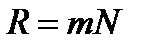 (31)
(31)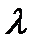 больше минимально возможной абсолютной погрешности
больше минимально возможной абсолютной погрешности 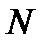 в формуле для разрешающей силы – это число щелей, принимающих участие в образовании главного максимума порядка
в формуле для разрешающей силы – это число щелей, принимающих участие в образовании главного максимума порядка 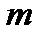 . Если поперечный размер падающего на решетку пучка света
. Если поперечный размер падающего на решетку пучка света 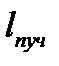 больше длины решетки
больше длины решетки 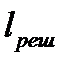 , то
, то 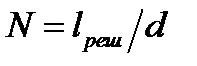 , где
, где 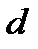 – постоянная решетки.
– постоянная решетки.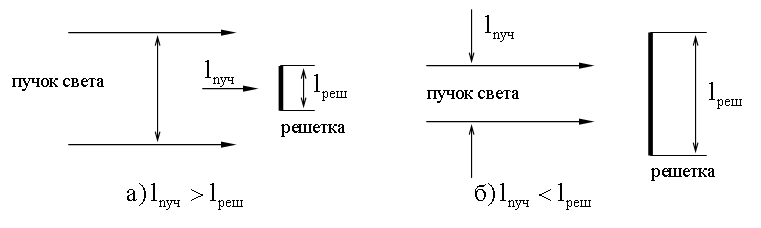
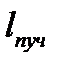 <
< 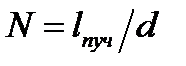
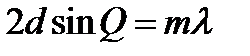 ,
, 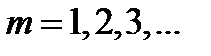 , (32)
, (32)


