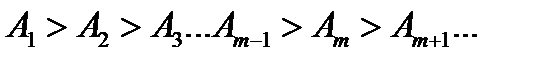Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая формулировка принципа Гюйгенса-Френеля
Пусть S – источник света (рис.4). Окружим его произвольной воображаемой поверхностью. Каждый участок этой поверхности можно считать источником вторичной волны. Вторичные волны от различных участков когерентны. Световая волна, являющаяся результатом интерференции вторичных волн, в пространстве вне поверхности совпадает с волной, излучаемой реальным источником света.
Рис. 4. К принципу Гюйгенса-Френеля Амплитуда
где
(3) - аналитическая запись принципа Гюйгенса - Френеля. В случае, когда между источником света и точкой наблюдения находится непрозрачная преграда с отверстием, то амплитуда вторичных волн в этих местах считается равной нулю.
Зоны Френеля
Вычисление интеграла по формуле (3) в общем случае затруднительно. Френель решил задачу нахождения амплитуды в т. Р, заменив интегрирование суммированием, т.е. перешёл от непрерывных сумм ( В случаях, если в задаче существует симметрия, амплитуду результирующего колебания можно найти методом зон Френеля, не прибегая к вычислению интеграла. Пусть от источника света S (рис. 5) распространяется монохроматическая сферическая волна, P –точка наблюдения.
Рис.5.Зоны Френеля
Через точку O проходит сферическая волновая поверхность. Она симметрична относительно прямой SP. Разобьем эту поверхность на кольцевые зоны I, II, III и т.д. так, чтобы расстояния от краев зоны до точки P отличались на Возьмем произвольную точку 1 в первой зоне Френеля. В зоне II найдется, в силу правила построения зон, такая соответствующая ей точка, что разность хода лучей, идущих в точку P от точек 1 и 2 будет равна
Из геометрических соображений следует, что при не очень больших номерах зон их площади примерно одинаковы. Значит, каждой точке первой зоны найдется соответствующая ей точка во второй, колебания которых погасят друг друга. Амплитуда результирующего колебания, приходящего в точку P от зоны с номером Происходит это из-за увеличения с ростом
|
|||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.85.72 (0.004 с.) |
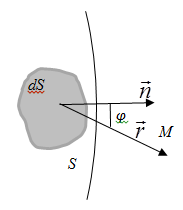
 колебаний, возбуждаемых в точке М вторичным источником, пропорциональна отношению площади
колебаний, возбуждаемых в точке М вторичным источником, пропорциональна отношению площади  участка волновой поверхности S к расстоянию
участка волновой поверхности S к расстоянию 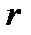 от него до точки М, и зависит от угла
от него до точки М, и зависит от угла 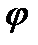 между внешней нормалью к волновой поверхности и направлением от элемента
между внешней нормалью к волновой поверхности и направлением от элемента 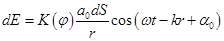 (2)
(2)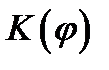 – коэффициент пропорциональности, удовлетворяющий неравенству
– коэффициент пропорциональности, удовлетворяющий неравенству 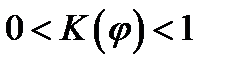 и убывающий с ростом угла
и убывающий с ростом угла 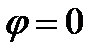
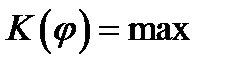 , при
, при 
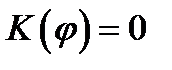 . Результирующее поле в точке М представляет собой суперпозицию колебаний (2), взятых для всей волновой поверхности:
. Результирующее поле в точке М представляет собой суперпозицию колебаний (2), взятых для всей волновой поверхности: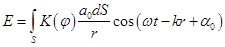 (3)
(3)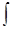 ) к дискретным (Σ).
) к дискретным (Σ).
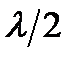 - половину длины световой волны. Построенные таким образом сектора сферы называются зонами Френеля.
- половину длины световой волны. Построенные таким образом сектора сферы называются зонами Френеля.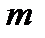 , уменьшается с ростом
, уменьшается с ростом