Дифракционные картины от различных препятствий

Из-за того, что длина световой волны очень мала, угол отклонения света от направления прямолинейного распространения невелик. Поэтому для отчетливого наблюдения дифракции нужно либо использовать очень маленькие препятствия, либо же располагать экран далеко от препятствий. При расстоянии между препятствием и экраном порядка метра размеры препятствии не должны превышать сотых долей миллиметра. Если же расстояние до экрана достигает сотен метров или нескольких километров, то дифракцию можно наблюдать на препятствиях размером в несколько сантиметров и даже метров.

На рис. 2 показано, как выглядят на фотографиях дифракционные картины от различных препятствий.

Рис. 2 Дифракционные картины от различных препятствий: а – от тонкой проволоки; б– от круглого отверстия; в– от круглого экрана

Вместо тени от проволочки видна группа светлых и темных полос; в центре дифракционной картины от отверстия появляется темное пятно, окруженное светлыми и темными кольцами (изменяя диаметр отверстия, можно в центре дифракционной картины получить и светлое пятно, окруженное темными и светлыми кольцами); в центре тени, образованной круглым экраном, видно светлое пятнышко, а сама тень окружена темными концентрическими кольцами.

 

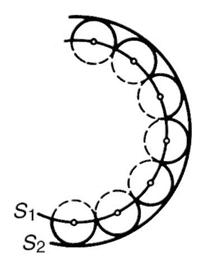
Принцип Гюйгенса-Френеля

Первая теория дифракции света, количественно описывавшая явление, предложена французским физиком Френелем. В основе теории лежит принцип Гюйгенса-Френеля. Гюйгенс, изучавший закономерности направления распространения волн, предположил, что каждую точку волнового фронта можно считать центром вторичных сферических волн, а волновой фронт в любой последующий момент времени – огибающей этих волн. Френель дополнил принцип Гюйгенса утверждением, что вторичные волны интерферируют между собой. Благодаря этому огибающая вторичных волн, введенная Гюйгенсом формально, приобрела физическое содержание как поверхность, где, благодаря взаимной интерференции вторичных волн, которые когерентны, результирующая волна имеет максимальную интенсивность.

Итак, принцип Гюйгенса-Френеля:

1. Каждая точка волновой поверхности, которой достигла в данный момент волна, является центром элементарных вторичных волн,их внешняя огибающая будет волновой поверхностью в последующий момент времени (рис.3); S₁ и S₂ - волновые поверхности соответственно в моменты t₁ и t₂; t₂ > t₁). (Х. Гюйгенс, 1678 г.).

Рис. 3. Источники вторичных волн

2. Амплитуда результирующей волны в любой точке пространства может быть найдена как результат интерференции всех вторичных волн, с учетом их фаз и амплитуд (О. Френель, 1818 г.).

Для того чтобы определить результат дифракции в некоторой точке пространства, следует рассчитать, согласно принципу Гюйгенса-Френеля, интерференцию вторичных волн, попавших в эту точку от волновой поверхности. Для волновой поверхности произвольной формы такой расчет достаточно сложен, но в отдельных случаях (сферическая или плоская волновая поверхность, симметричное расположение точки относительно волновой поверхности и непрозрачной преграды) вычисления сравнительно просты. Волновую поверхность при этом разбивают на отдельные участки (зоны Френеля), расположенные определенным образом, что упрощает математические операции.