
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование дифракции Френеля на круглом отверстииСодержание книги
Поиск на нашем сайте
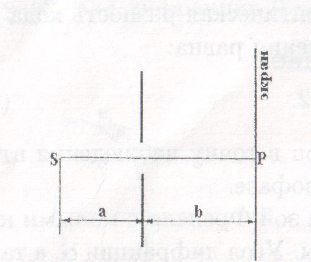
Цель работы: изучение дифракции Френеля на круглом отверстии и определение радиуса отверстия. Оборудование: лазер, микрообъектив, диафрагма с отверстием, экран. Зоны Френеля В ряде случаев удобно в качестве поверхности На рис. 1 S – источник света; P – точка наблюдения; буквой B 1 P = B 2 P = B 3 P = ……………… где
Рис. 1. Деление волнового фронта на зоны Френеля Через точки Bi проводим плоскости, перпендикулярные прямой SP и плоскости чертежа. Пересекая волновой фронт, эти плоскости делят его на участки, которые называются зонами Френеля. Каждая зона Френеля является источником вторичной волны. Из построения следует, что оптическая разность хода
Следовательно, от соседних зон в точку наблюдения вторичные волны приходят в противофазе. Можно показать, что площади зон Френеля с малыми номерами не зависят от номера зоны. Угол дифракции
амплитуды вторичных волн медленно убывают с ростом номера зоны. Используя векторный метод сложения колебаний, получаем, что амплитуда
Этот знакопеременный ряд можно преобразовать следующим образом:
Так как амплитуды медленно убывают с увеличением номера зоны, то выражения в скобках приблизительно равны нулю. Тогда Обозначим амплитуду в точке P при полностью открытом фронте
Поместим между источником света S и экраном непрозрачную диафрагму с круглым отверстием (рис.2). Предположим, что размер отверстия можно менять. Точка наблюдения P находится напротив центра отверстия. Пусть отверстие открывает только первую зону Френеля. Тогда амплитуда в точке P возрастает в два раза по сравнению с амплитудой при полностью открытом волновом фронте: При удалении от P вдоль экрана вверх или вниз интенсивность будет монотонно убывать – дифракционная картина на экране будет представлять собой светлый кружок. При расширении отверстия в точку P начнут приходить вторичные волны, интерференция которых с волнами, приходящими от точек первой зоны Френеля, вызовет уменьшение интенсивности в точке P. Вокруг точки P начнет образовываться светлое кольцо, к которому перейдет максимум интенсивности. Когда отверстие откроет две первые зоны Френеля, вторичные волны от них в точке P практически полностью уничтожат друг друга из-за интерференции. На экране получится картина, состоящая из томного пятна, окруженного светлым
Рис. 2. Схема для наблюдения дифракции Френеля на круглом отверстии. При дальнейшем увеличении размеров отверстия действия двух первых зон Френеля в точке P остаются скомпенсированными. Все поле в точке P создается только частью третьей зоны Френеля. В центре картины появляется светлое пятнышко, а центральный темный кружок расширяется и переходит в темное кольцо, окружающее это пятнышко. Когда число На рис. 3 схематически для различных
Рис.3. Распределение интенсивности в зависимости от расстояния до центра картины
Рис.4.Дифракционные картины при различных значениях Можно показать, что радиус
Таким образом, зная
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.76 (0.009 с.) |

 , заменяющей реальный источник света, выбрать сферу с центром в точке, где расположен источник. В некоторый момент времени сфера является волновым фронтом, поэтому в дальнейшем будем называть ее волновым фронтом.
, заменяющей реальный источник света, выбрать сферу с центром в точке, где расположен источник. В некоторый момент времени сфера является волновым фронтом, поэтому в дальнейшем будем называть ее волновым фронтом.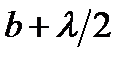 ,
,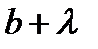 , (1)
, (1)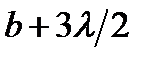 ,
,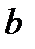 – расстояние от P до волнового фронта,
– расстояние от P до волнового фронта, 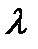 – длина световой волны, которую излучает источник (при этом предполагается, что источник и точка наблюдения находятся в вакууме и λ – длина волны в вакууме).
– длина световой волны, которую излучает источник (при этом предполагается, что источник и точка наблюдения находятся в вакууме и λ – длина волны в вакууме).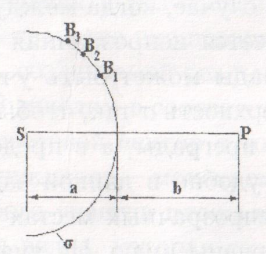
 от соседних зон до точки наблюдения равна:
от соседних зон до точки наблюдения равна: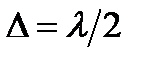 (2)
(2)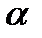 , а также расстояния от зоны до точки наблюдения медленно увеличиваются с ростом номера зоны. Следовательно, согласно
, а также расстояния от зоны до точки наблюдения медленно увеличиваются с ростом номера зоны. Следовательно, согласно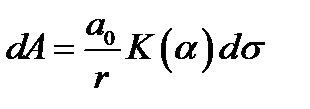 (3)
(3)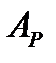 световой волны в точке наблюдения P равна:
световой волны в точке наблюдения P равна: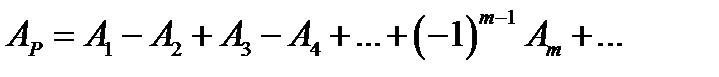 (4)
(4)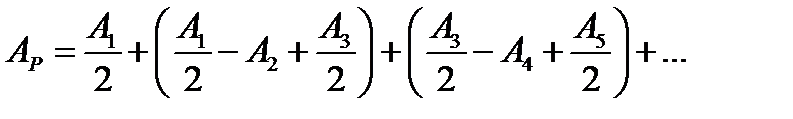 (5)
(5)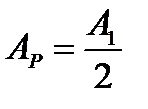 .
.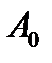 :
: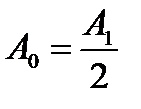 (6)
(6)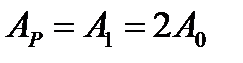 , а интенсивность возрастает в четыре раза по сравнению с интенсивностью при полностью открытом волновом фронте:
, а интенсивность возрастает в четыре раза по сравнению с интенсивностью при полностью открытом волновом фронте: 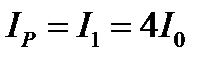 .
. кольцом.
кольцом. открытых зон равно трем, интенсивность в точке P будет такой же, какая получилась бы, если бы была открыта только одна третья зона. Картина на экране состоит из светлого пятна, окруженного темным и светлыми кольцами. При
открытых зон равно трем, интенсивность в точке P будет такой же, какая получилась бы, если бы была открыта только одна третья зона. Картина на экране состоит из светлого пятна, окруженного темным и светлыми кольцами. При 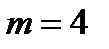 светлый центр сменится темным. Вообще, при нечетном
светлый центр сменится темным. Вообще, при нечетном 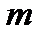 центр дифракционной картины будет светлым, а при четном
центр дифракционной картины будет светлым, а при четном 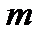 центр дифракционной картины будет темным.
центр дифракционной картины будет темным. 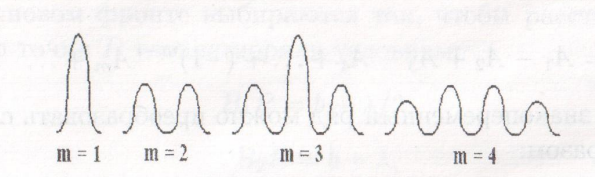

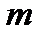
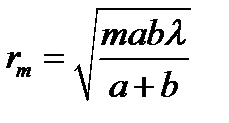 (7)
(7)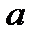 ,
, 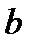 и
и 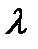 , можно вычислить радиус отверстия.
, можно вычислить радиус отверстия.


