Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Детерминированные автоматы с магазинной памятьюСодержание книги
Поиск на нашем сайте
Определение 12.1.1. Будем говорить, что два перехода МП-автомата 1. p1 = p2; 2. 3. Определение 12.1.2. МП-автомат называется детерминированным (deterministic), если он имеет ровно одно начальное состояние и все переходы этого автомата попарно несовместны. Пример 12.1.3. МП-автомат M из примера 10.2.8 не является детерминированным, так как переходы Определение 12.1.4. Язык L над алфавитом Пример 12.1.5. Рассмотрим алфавит Пример 12.1.6. Язык L, распознаваемый МП-автоматом M из примера 10.2.8, является детерминированным контекстно-свободным языком, так как язык
где
Упражнение 12.1.7. Является ли детерминированным контекстно-свободный язык 12.2*. Свойства класса детерминированных языков Теорема 12.2.1. Каждый автоматный язык является детерминированным контекстно-свободным языком. Доказательство. Утверждение следует из теоремы 2.7.1. Лемма 12.2.2. Каждый детерминированный МП-автомат Доказательство. Пусть дан детерминированный МП-автомат
натуральное число Шаг индукции. Пусть существует переход
с положительным избытком. Рассмотрим четыре случая. Случай 1. Случай 2.
Случай 3. Существует переход Случай 4. Существуют переход Лемма 12.2.3. Каждый детерминированный МП-автомат Доказательство. Сначала применим лемму 12.2.2, затем преобразуем МП-автомат так, чтобы для каждого перехода Лемма 12.2.4. Пусть
удовлетворяет условиям Доказательство. Применив лемму 12.2.3, получим детерминированный МП-автомат
Теорема 12.2.5. Язык
Доказательство. Достаточность проверяется легко. Докажем необходимость. Рассмотрим МП-автомат
о котором говорится в лемме 12.2.4. Для любых
Очевидно, что Построим искомый МП-автомат
(Напоминаем, что через Индукцией по количеству тактов работы можно доказать, что
тогда и только тогда, когда
и
для каждого Теорема 12.2.6. Пусть L - детерминированный контекстно-свободный язык. Тогда язык L не является существенно неоднозначным. Доказательство. Пусть дан детерминированный контекстно-свободный язык L. Рассмотрим МП-автомат
о котором говорится в лемме 12.2.4. Применив к этому МП-автомату конструкцию из доказательства теоремы 10.2.7, получим однозначную контекстно-свободную грамматику G, порождающую язык
Так как МП-автомат M не содержит переходов, ведущих из Q2 в Q1, а символ Теорема 12.2.7. Дополнение каждого детерминированного контекстно-свободного языка является детерминированным контекстно-свободным языком. Доказательство можно найти в [7, c. 110-116] или [2, c. 212-217]. Пример 12.2.8. Язык Теорема 12.2.9. Неверно, что для любых детерминированных контекстно-свободных языков L1 и L2 язык Доказательство. Достаточно рассмотреть детерминированные контекстно-свободные языки L1 и L2 из доказательства теоремы 9.5.1. Теорема 12.2.10. Неверно, что для любых детерминированных контекстно-свободных языков L1 и L2 язык Доказательство. Утверждение следует из теорем 12.2.7 и 12.2.9 и закона де Моргана. Упражнение 12.2.11. Является ли детерминированным контекстно-свободный язык В этой лекции даются формальные определения, связанные с прямыми (то есть читающими входную строку слева направо) синтаксическими анализаторами. В первом разделе доказывается, что для языков из класса LL(1) можно построить основанный на детерминированном автомате с магазинной памятью анализатор, который создает дерево разбора, двигаясь снизу вверх, то есть от листьев к корню (в теории контекстно-свободных грамматик принято изображать деревья с корнем наверху). Во втором разделе формулируется аналогичный результат об анализе сверху вниз для грамматик из класса Нисходящий разбор Определение 13.1.1. Процесс нахождения дерева вывода слова w в заданной контекстно-свободной грамматике называется синтаксическим разбором или синтаксическим анализом (parsing). Определение 13.1.2. Протоколом левостороннего вывода в контекстно-свободной грамматике
является последовательность
где для каждого i < n, если Пример 13.1.3. Рассмотрим контекстно-свободную грамматику
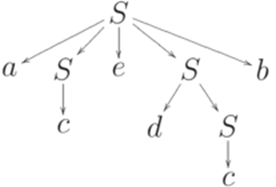
Дереву вывода
соответствует левосторонний вывод
Протоколом этого вывода является последовательность
Лемма 13.1.4. Разным левосторонним выводам в одной и той же контекстно-свободной грамматике соответствуют разные протоколы. Замечание 13.1.5. Протокол левостороннего вывода в контекстно-свободной грамматике является естественным описанием соответствующего дерева вывода в порядке префиксного обхода (preorder traversal). (При префиксном обходе упорядоченного дерева первым посещается корень этого дерева, затем выполняется префиксный обход первого непосредственного потомка корня, затем второго и т. д.)
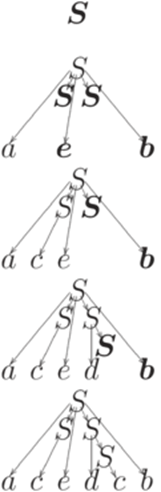
Например, протокол левостороннего вывода из примера 13.1.3 задает процесс постепенного конструирования дерева вывода, изображенный ниже.
Определение 13.1.6. Левым разбором (left parse) слова w в контекстно-свободной грамматике G называется протокол любого левостороннего вывода слова w в грамматике G. Пример 13.1.7. Левым разбором слова aceaacecbecbbв грамматике из примера 13.1.3 является последовательность
Определение 13.1.8. Процесс нахождения левого разбора слова w в заданной контекстно-свободной грамматике Gназывается нисходящим разбором (top-down parsing). Определение 13.1.9. Вычислительным процессом МП-автомата M будем называть конечную последовательность его конфигураций, каждая из которых (кроме первой) получается из предыдущей одним тактом работы автомата M. Пример 13.1.10. Рассмотрим МП-автомат
из примера 10.2.8. Последовательность
является вычислительным процессом этого МП-автомата. Определение 13.1.11. Если в некотором вычислительном процессе МП-автомата Пример 13.1.12. Вычислительный процесс из примера 13.1.10 допускает слово bab. Замечание 13.1.13. МП-автомат M допускает слово Определение 13.1.14. Протоколом вычислительного процесса МП-Автомата
является последовательность переходов
где для каждого i между 1 и n слово xi определяется равенством
для некоторого слова Пример 13.1.15. Протоколом вычислительного процесса из примера 13.1.10 является последовательность
Определение 13.1.16. Для каждой контекстно-свободной грамматики Пример 13.1.17. Рассмотрим контекстно-свободную грамматику G с терминальным алфавитом
Ей соответствует следующая грамматика
Замечание 13.1.18. Очевидно, что Лемма 13.1.19. Если Доказательство. Очевидно, что если Теперь докажем индукцией по длине вывода, что если Если Если
равенство
невозможен, так как предположение индукции дает Определение 13.1.20. Пусть даны контекстно-свободная грамматика Пример 13.1.21. Рассмотрим контекстно-свободную грамматику
и
Легко убедиться, что МП-автомат M является нисходящим магазинным анализатором для грамматики G из примера 13.1.17. Определение 13.1.22. Сентенциальной формой (sentential form) грамматики Пример 13.1.23. Слова S, aSeaceSbb, aceaacecbecbb являются сентенциальными формами грамматики из примера 13.1.3. Определение 13.1.24. Пусть дана контекстно-свободная грамматика Функция FIRST ставит в соответствие каждому слову
Функция FOLLOW ставит в соответствие каждому нетерминальному символу A множество тех терминальных символов, которые могут встречаться в сентенциальных формах непосредственно справа от A, то есть
Функция DIRECTOR ставит в соответствие каждому правилу
иначе
Пример 13.1.25. Рассмотрим контекстно-свободную грамматику из примера 13.1.3. Очевидно, что
Пример 13.1.26. Рассмотрим контекстно-свободную грамматику
Пример 13.1.27. Пусть контекстно-свободная грамматика
равносильно тому, что найдутся такие
Теорема 13.1.28. Пусть дана контекстно-свободная грамматика
Тогда МП-автомат M является нисходящим магазинным анализатором для грамматики G. Доказательство. Индукцией по количеству тактов можно доказать, что если
С другой стороны, докажем, что если в грамматике Проведем доказательство индукцией по сумме длины слова bw и длины вывода
где
Шаг индукции доказан. Теперь легко проверить, что выполняется Гомоморфизм
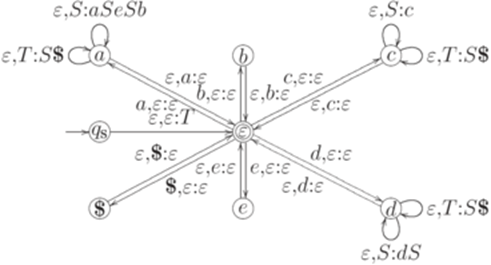
Пример 13.1.29. Рассмотрим контекстно-свободную грамматику из примера 13.1.3. Грамматика с маркером конца строки имеет правила
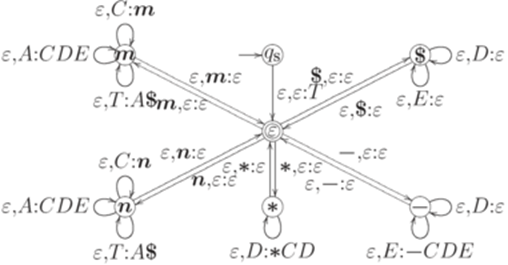
Соответствующий нисходящий магазинный анализатор M, построенный в теореме 13.1.28, имеет приведенный ниже вид.
Определение 13.1.30. Контекстно-свободная грамматика Замечание 13.1.31. Первая буква L в названии класса LL(1) означает, что входное слово читается слева направо (left-to-right). Вторая буква L означает, что строится левосторонний вывод (leftmost derivation). Число 1 указывает на то, что на каждом шаге для принятия решения используется один символ неразобранной части входного слова. Пример 13.1.32. Грамматика из примера 13.1.3 принадлежит классу LL(1), а грамматика из примера 3.1.17 этому классу не принадлежит. Теорема 13.1.33. МП-автомат M, построенный в теореме 13.1.28 по контекстно-свободной грамматике G, является детерминированным тогда и только тогда, когда грамматика G принадлежит классу LL(1). Теорема 13.1.34. Грамматики из класса LL(1) порождают только детерминированные контекстно-свободные языки. Теорема 13.1.35. Пусть контекстно-свободная грамматика 1. если 2. если 3. если Теорема 13.1.36. Пусть контекстно-свободная грамматика 1. если 2. если
Замечание 13.1.37. Теоремы 13.1.35 и 13.1.36 дают алгоритм проверки принадлежности контекстно-свободной грамматики G классу LL(1). Можно предположить, что грамматика G не содержит бесполезных символов (их можно устранить). Сначала необходимо вычислить значения Затем необходимо вычислить значения В заключение вычислим значения Теорема 13.1.38. Пусть даны контекстно-свободная грамматика
где множество P0 не содержит правил с левой частью A и ни одно из слов
Пример 13.1.39. Если к контекстно-свободной грамматике
После упрощения получаем грамматику G'' с правилами
Язык L(G'') распознается детерминированным МП-автоматом
Можно доказать, что МП-автомат M является нисходящим магазинным анализатором для грамматики
Пример 13.1.40. Пусть
Грамматика с маркером конца строки имеет правила
Соответствующий нисходящий магазинный анализатор M, построенный в теореме 13.1.28, имеет приведенный ниже вид.
Легко убедиться, что грамматика G принадлежит классу LL(1) и МП-автомат M является детерминированным. Упражнение 13.1.41. Существует ли детерминированный нисходящий магазинный анализатор для грамматики
Упражнение 13.1.42. Принадлежит ли грамматика
классу LL(1)? Упражнение 13.1.43. Принадлежит ли грамматика
классу LL(1)? Восходящий разбор Определение 13.2.1. Протоколом правостороннего вывода в контекстно-свободной грамматике
является последовательность
где для каждого i<n, если Пример 13.2.2. Рассмотрим контекстно-свободную грамматику
и дерево вывода
из примера 13.1.3. Этому дереву вывода соответствует правосторонний вывод
Протоколом этого вывода является последовательность
| |||||||
|
| Поделиться: |

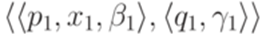 и
и 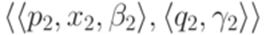 являются совместными, если
являются совместными, если или
или  ;
; или
или  .
.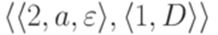 и
и  совместны.
совместны.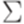 называется детерминированным контекстно-свободным языком, если существует детерминированный МП-автомат, распознающий язык
называется детерминированным контекстно-свободным языком, если существует детерминированный МП-автомат, распознающий язык 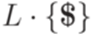 над алфавитом
над алфавитом 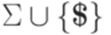 , где
, где 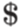 - дополнительный символ, не принадлежащий множеству
- дополнительный символ, не принадлежащий множеству 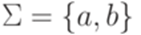 . Язык
. Язык  - детерминированный контекстно-свободный язык, так как язык
- детерминированный контекстно-свободный язык, так как язык 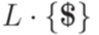 порождается детерминированным МП-автоматом (хотя язык L не порождается никаким детерминированным МП-автоматом).
порождается детерминированным МП-автоматом (хотя язык L не порождается никаким детерминированным МП-автоматом).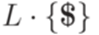 порождается детерминированным МП-автоматом
порождается детерминированным МП-автоматом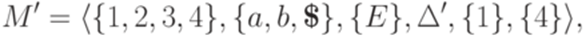
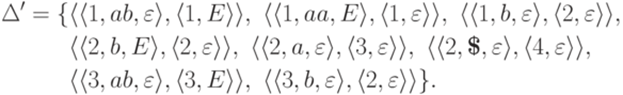
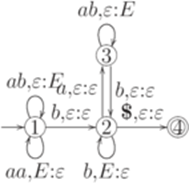
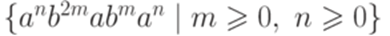 ?
?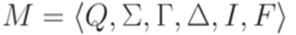 эквивалентен некоторому детерминированному МП-автомату
эквивалентен некоторому детерминированному МП-автомату 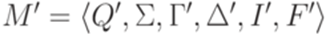 , где для каждого перехода
, где для каждого перехода 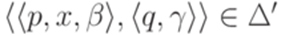 выполняется неравенство
выполняется неравенство 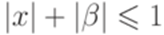 .
.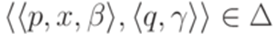
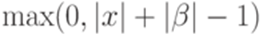 . Докажем лемму индукцией по сумме избытков всех переходов.
. Докажем лемму индукцией по сумме избытков всех переходов.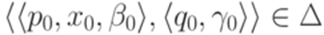
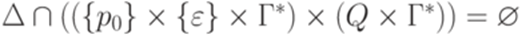 . Обозначим первый символ слова x0 через a0. Преобразуем МП-автомат M в эквивалентный ему детерминированный МП-автомат с меньшей суммой избытков всех переходов. Для этого добавим новое состояние r и переход
. Обозначим первый символ слова x0 через a0. Преобразуем МП-автомат M в эквивалентный ему детерминированный МП-автомат с меньшей суммой избытков всех переходов. Для этого добавим новое состояние r и переход 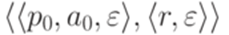 . Каждый переход вида
. Каждый переход вида 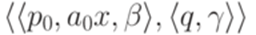 заменим на переход
заменим на переход 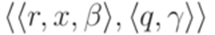 . К полученному таким образом детерминированному МП-автомату применимо предположение индукции.
. К полученному таким образом детерминированному МП-автомату применимо предположение индукции. . Обозначим первый символ слова
. Обозначим первый символ слова 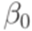 через C0. Преобразуем МП-автомат M в эквивалентный ему детерминированный МП-автомат с меньшей суммой избытков всех переходов. Для этого добавим новое состояние r и переход
через C0. Преобразуем МП-автомат M в эквивалентный ему детерминированный МП-автомат с меньшей суммой избытков всех переходов. Для этого добавим новое состояние r и переход 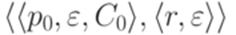 . Каждый переход вида
. Каждый переход вида 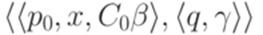 заменим на переход
заменим на переход 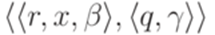 . К полученному таким образом детерминированному МП-автомату применимо предположение индукции.
. К полученному таким образом детерминированному МП-автомату применимо предположение индукции.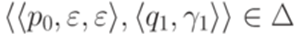 . Тогда переходы
. Тогда переходы 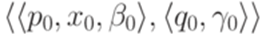 и
и 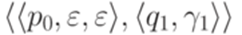 совместны. Противоречие.
совместны. Противоречие.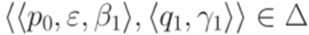 и переход
и переход 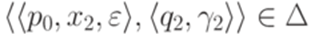 , где
, где 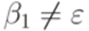 и
и 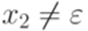 . Тогда переходы
. Тогда переходы 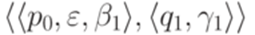 и
и  совместны. Противоречие.
совместны. Противоречие.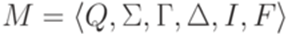 эквивалентен некоторому детерминированному МП-автомату
эквивалентен некоторому детерминированному МП-автомату 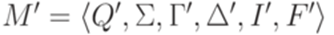 , где каждый переход
, где каждый переход 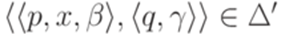 удовлетворяет условиям
удовлетворяет условиям 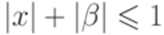 и
и 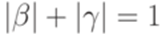 .
.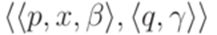 выполнялось неравенство
выполнялось неравенство  (см. пример 10.2.4), и в заключение заменим каждый переход вида
(см. пример 10.2.4), и в заключение заменим каждый переход вида 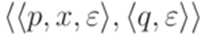 на два последовательных перехода (см. пример 10.2.5).
на два последовательных перехода (см. пример 10.2.5).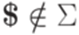 ,
, 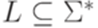 и язык
и язык 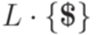 порождается некоторым детерминированным МП-автоматом. Тогда этот язык порождается также некоторым детерминированным МП-автоматом
порождается некоторым детерминированным МП-автоматом. Тогда этот язык порождается также некоторым детерминированным МП-автоматом 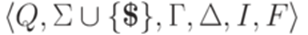 , где
, где  ,
,  ,
,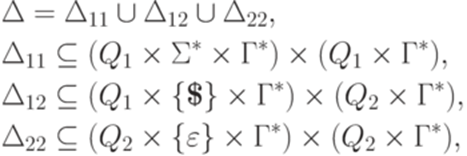
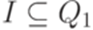 ,
, 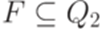 и каждый переход
и каждый переход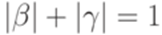 .
.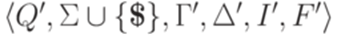 . Построим искомый МП-автомат
. Построим искомый МП-автомат 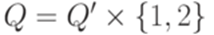 ,
, 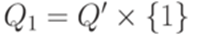 ,
, 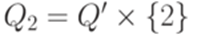 ,
,  ,
, 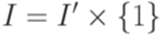 ,
, 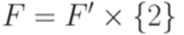 ,
,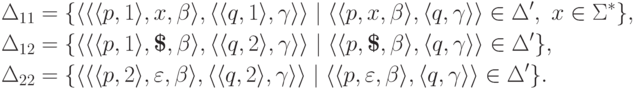
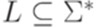 является детерминированным контекстно-свободным языком тогда и только тогда, когда найдется такой детерминированный МП-автомат
является детерминированным контекстно-свободным языком тогда и только тогда, когда найдется такой детерминированный МП-автомат 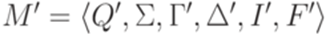 , что
, что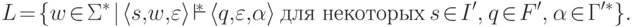
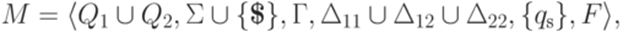
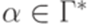 и
и 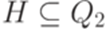 введем обозначение
введем обозначение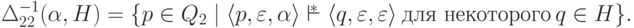
 для любых
для любых 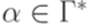 ,
, 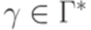 и
и 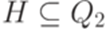 .
.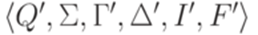 , положив
, положив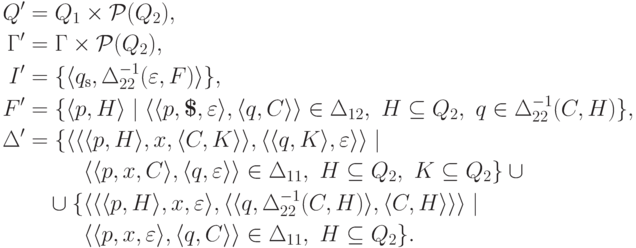
 обозначается множество всех подмножеств множества Q2.)
обозначается множество всех подмножеств множества Q2.)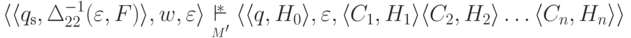


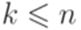 .
.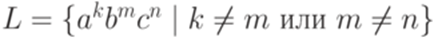 над алфавитом {a,b,c} не является детерминированным контекстно-свободным языком, так как его дополнение не является контекстно-свободным.
над алфавитом {a,b,c} не является детерминированным контекстно-свободным языком, так как его дополнение не является контекстно-свободным.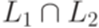 тоже является детерминированным контекстно-свободным языком.
тоже является детерминированным контекстно-свободным языком.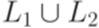 тоже является детерминированным контекстно-свободным языком.
тоже является детерминированным контекстно-свободным языком.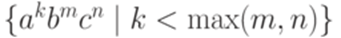 ?
? . При этом понятие анализа снизу вверх формализовано в терминах последовательности правил, примененных в левостороннем выводе, а понятие анализа сверху вниз - в терминах обращенной последовательности правил, примененных в правостороннем выводе.
. При этом понятие анализа снизу вверх формализовано в терминах последовательности правил, примененных в левостороннем выводе, а понятие анализа сверху вниз - в терминах обращенной последовательности правил, примененных в правостороннем выводе.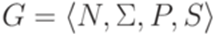 будем называть последовательность правил, примененных в этом выводе. Формально говоря, протоколом левостороннего вывода
будем называть последовательность правил, примененных в этом выводе. Формально говоря, протоколом левостороннего вывода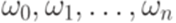
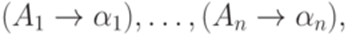
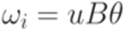 и
и  для некоторых
для некоторых 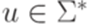 ,
, 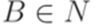 ,
, 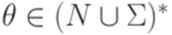 ,
, 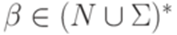 , то Ai+1 = B и
, то Ai+1 = B и 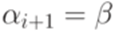 .
.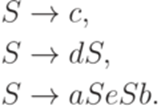
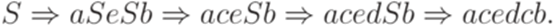
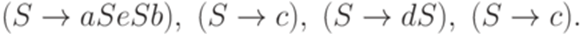
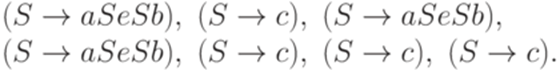
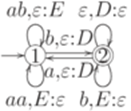
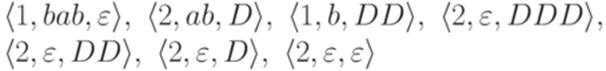
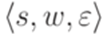 , где
, где 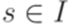 и
и 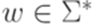 , а последняя конфигурация имеет вид
, а последняя конфигурация имеет вид 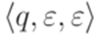 , где
, где 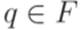 , то будем говорить, что этот вычислительный процесс допускает слово w.
, то будем говорить, что этот вычислительный процесс допускает слово w.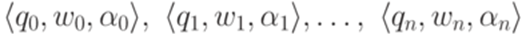

 , а через
, а через 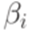 и
и 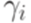 обозначены кратчайшие слова из
обозначены кратчайшие слова из 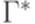 , удовлетворяющие условиям
, удовлетворяющие условиям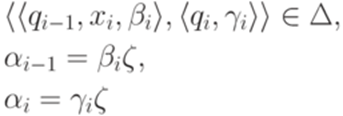
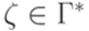 .
.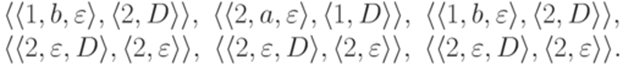
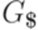 контекстно-свободную грамматику
контекстно-свободную грамматику 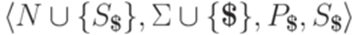 , где
, где 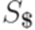 - два различных новых символа, не принадлежащие множеству
- два различных новых символа, не принадлежащие множеству  , и
, и 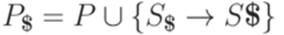 . Грамматику
. Грамматику 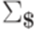 . Нетерминальный алфавит
. Нетерминальный алфавит 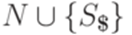 будем обозначать через
будем обозначать через 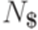 .
.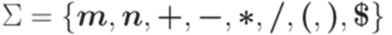 , вспомогательным алфавитом N = {S,A,B,C} и правилами
, вспомогательным алфавитом N = {S,A,B,C} и правилами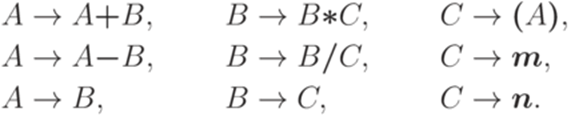
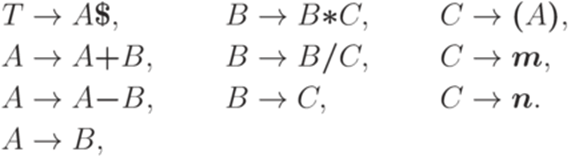
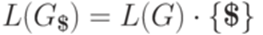 .
.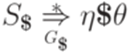 , где
, где 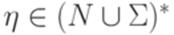 и
и  .
.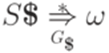 , то слово
, то слово 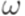 не содержит символа
не содержит символа 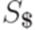 .
.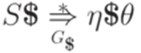 , то
, то 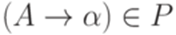 .
. , то
, то  , что невозможно (очевидно, что если
, что невозможно (очевидно, что если  , то рассмотрим два случая. При
, то рассмотрим два случая. При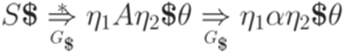
 обеспечивается предположением индукцией. Случай
обеспечивается предположением индукцией. Случай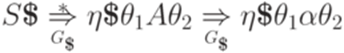
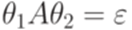 .
.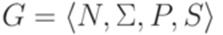 и МП-автомат
и МП-автомат  и существует такой гомоморфизм
и существует такой гомоморфизм 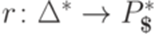 , что для каждого вычислительного процесса (МП-автомата M), допускающего слово
, что для каждого вычислительного процесса (МП-автомата M), допускающего слово 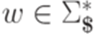 , образ протокола этого вычислительного процесса при гомоморфизме
, образ протокола этого вычислительного процесса при гомоморфизме 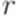 является протоколом некоторого левостороннего вывода слова w в грамматике
является протоколом некоторого левостороннего вывода слова w в грамматике  и
и 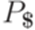 рассматриваются как два алфавита.)
рассматриваются как два алфавита.)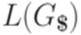 распознается недетерминированным МП-автоматом
распознается недетерминированным МП-автоматом 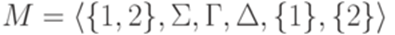 , где
, где
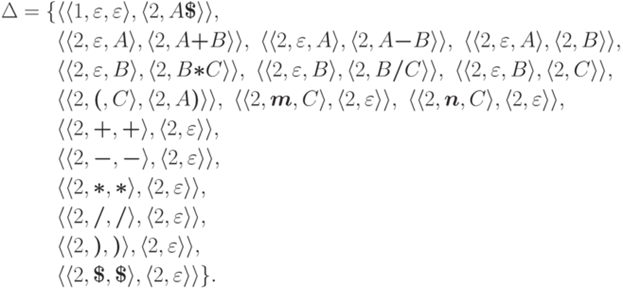
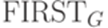 ,
, 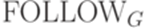 и
и 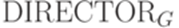 , связанные с грамматикой G. Для краткости будем писать просто FIRST, FOLLOW и DIRECTOR.
, связанные с грамматикой G. Для краткости будем писать просто FIRST, FOLLOW и DIRECTOR.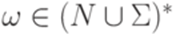 множество тех терминальных символов, с которых начинаются слова, выводимые из
множество тех терминальных символов, с которых начинаются слова, выводимые из 
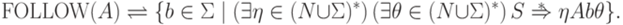
 , то
, то
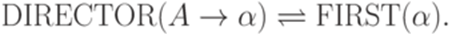
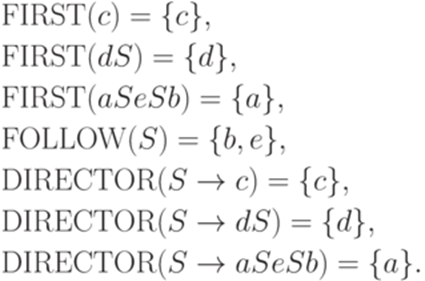
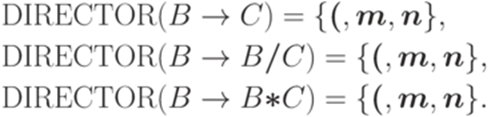
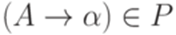 и символ
и символ 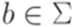 . Тогда утверждение
. Тогда утверждение
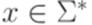 ,
,  и
и 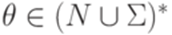 , что
, что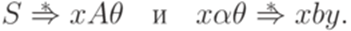
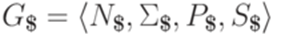 - соответствующая контекстно-свободная грамматика с маркером конца строки, приведенная в определении 13.1.16. Обозначим через M МП-автомат
- соответствующая контекстно-свободная грамматика с маркером конца строки, приведенная в определении 13.1.16. Обозначим через M МП-автомат  , где
, где
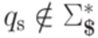 ,
, 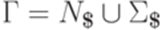 и
и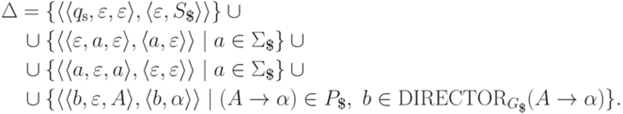
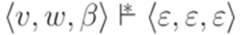 , где
, где  , то
, то 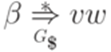 . Следовательно,
. Следовательно, 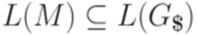 .
. и
и  , где
, где  ,
, 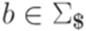 ,
, 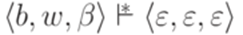 .
.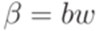 образует базис индукции (очевидно, что
образует базис индукции (очевидно, что 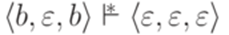 ). Проверим теперь шаг индукции. Так как
). Проверим теперь шаг индукции. Так как  и
и 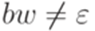 , то
, то 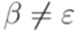 . Если
. Если 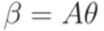 , где
, где 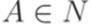 , то вывод
, то вывод 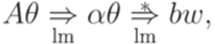
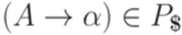 и в силу леммы 13.1.27
и в силу леммы 13.1.27  . Отсюда получаем, что
. Отсюда получаем, что 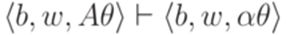 , и остается применить предположение индукции для левосторонних выводов
, и остается применить предположение индукции для левосторонних выводов  и
и  . Если же
. Если же 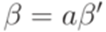 , где
, где  , то, очевидно, a = b и
, то, очевидно, a = b и  . Если
. Если  , то
, то  и в силу леммы 13.1.19
и в силу леммы 13.1.19  , но этот случай уже рассмотрен в базисе индукции. Пусть
, но этот случай уже рассмотрен в базисе индукции. Пусть  . Тогда w = b'w' для некоторых
. Тогда w = b'w' для некоторых  и
и 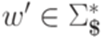 . Обозначим u' = ub. Применяя предположение индукции для левосторонних выводов
. Обозначим u' = ub. Применяя предположение индукции для левосторонних выводов  и
и  , получаем
, получаем 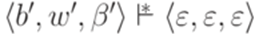 . Согласно построению МП-автомата M имеем
. Согласно построению МП-автомата M имеем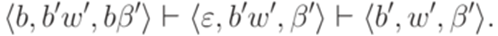
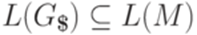 .
.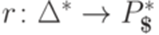 задается соотношениями
задается соотношениями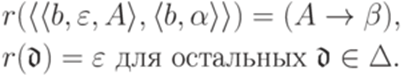
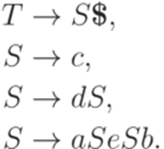
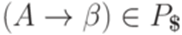 , где
, где 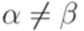 , множества
, множества 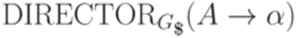 и
и 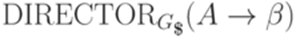 не пересекаются.
не пересекаются. (где
(где  , то
, то  для всех
для всех  ;
;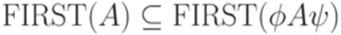 для всех
для всех  ;
; .
.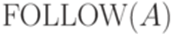 (где
(где 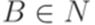 и
и 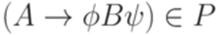 , то
, то 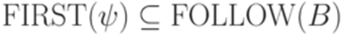 ;
; , то
, то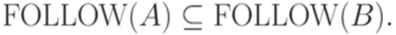
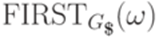 параллельно для всех слов
параллельно для всех слов 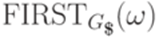 (начав с пустых множеств), используя условия, приведенные в теореме 13.1.35.
(начав с пустых множеств), используя условия, приведенные в теореме 13.1.35. параллельно для всех вспомогательных символов A. Для этого постепенно пополняем множества
параллельно для всех вспомогательных символов A. Для этого постепенно пополняем множества 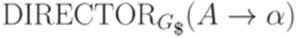 для всех правил
для всех правил 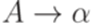 , следуя определению функции
, следуя определению функции 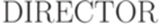 , и проверим условия из определения 13.1.30.
, и проверим условия из определения 13.1.30.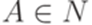 . Пусть
. Пусть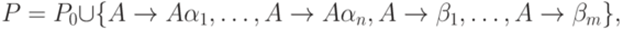
 не начинается с символа A. Тогда грамматика G эквивалентна контекстно-свободной грамматике
не начинается с символа A. Тогда грамматика G эквивалентна контекстно-свободной грамматике 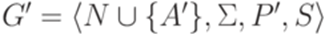 , где A' - новый символ, не принадлежащий множеству
, где A' - новый символ, не принадлежащий множеству 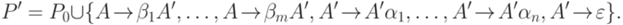
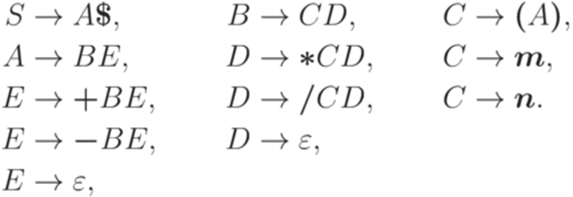
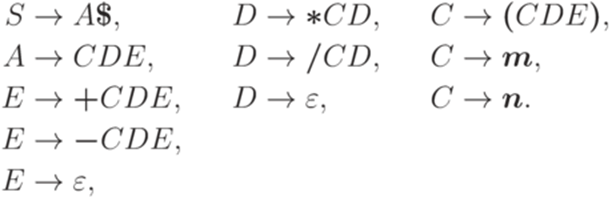
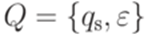 ,
, 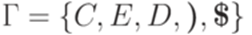 ,
, 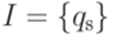 ,
, 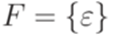 и
и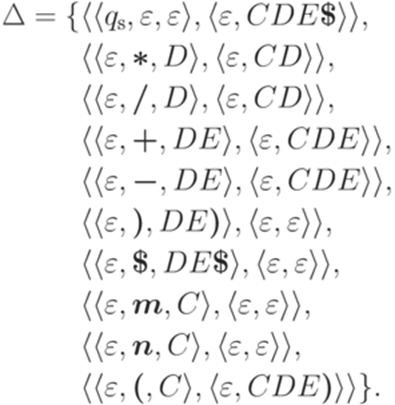
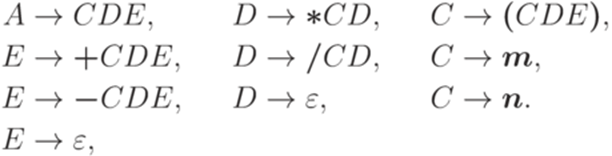
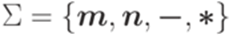 и
и 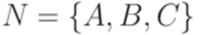 . Рассмотрим контекстно-свободную грамматику G с правилами
. Рассмотрим контекстно-свободную грамматику G с правилами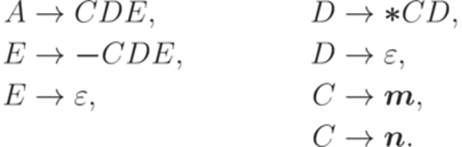
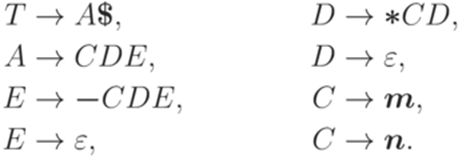
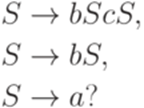
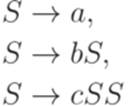
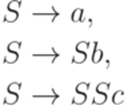
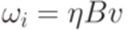 и
и  для некоторых
для некоторых 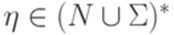 ,
, 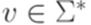 ,
, 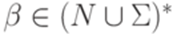 , то An-i = B и
, то An-i = B и 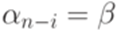 .
.