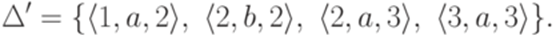Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конфигурация конечного автомата
Определение 2.2.1. Конфигурацией или мгновенным описанием (instantaneous description) конечного автомата Замечание 2.2.2. Содержательно конфигурация представляет собой "мгновенное описание" конечного автомата. Если представить, что исходное слово, принадлежность которого рассматриваемому языку надо проверить, дано в некотором "входном потоке", то в конфигурации Определение 2.2.3. Определим на множестве всех конфигураций конечного автомата M бинарное отношение Пример 2.2.4. Рассмотрим конечный автомат
из примера 2.1.2. Тогда Определение 2.2.5. Бинарное отношение Пример 2.2.6. Для конечного автомата из примера 2.1.2 выполняется Лемма 2.2.7. Пусть дан конечный автомат Лемма 2.2.8. Если Доказательство. Лемму легко доказать индукцией по количеству тактов в вычислительном процессе, ведущем из конфигурации Конечные автоматы с однобуквенными переходами Лемма 2.3.1. Каждый автоматный язык распознается некоторым конечным автоматом, не содержащим переходов с метками длины больше единицы и имеющим ровно одно начальное состояние и ровно одно заключительное состояние. Пример 2.3.2. Рассмотрим язык, заданный конечным автоматом
Тот же язык распознается конечным автоматом
Здесь первые два перехода заменяют старый переход Лемма 2.3.3. Каждый автоматный язык распознается некоторым конечным автоматом, содержащим только переходы с метками длины единица и имеющим ровно одно начальное состояние. Доказательство. Согласно лемме 2.3.1 можно предположить, что исходный язык задан конечным автоматом
Пример 2.3.4. Пусть
Легко убедиться, что
|
|||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 90; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.93.73 (0.006 с.) |
 называется любая упорядоченная пара
называется любая упорядоченная пара 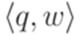 , где
, где  и
и 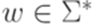 .
.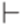 (такт работы (step)) следующим образом. Если
(такт работы (step)) следующим образом. Если 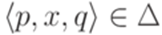 и
и 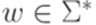 , то
, то  . Иногда вместо
. Иногда вместо  .
.
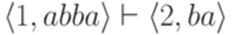 .
. определяется как рефлексивное, транзитивное замыкание отношения
определяется как рефлексивное, транзитивное замыкание отношения 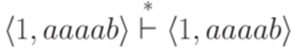 и
и 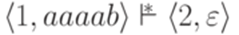 .
.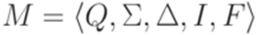 . Слово
. Слово 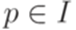 и
и 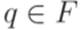 верно
верно 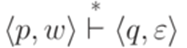 .
.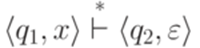 и
и  , то
, то 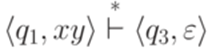 .
.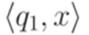 в конфигурацию
в конфигурацию 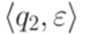 .
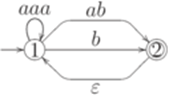
. , где Q = {1,2},
, где Q = {1,2}, 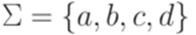 , I = {1,2}, F = {1,2},
, I = {1,2}, F = {1,2},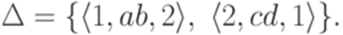
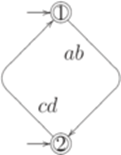
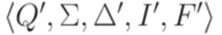 , где Q' = {0,1,2,3,4,5}, I' = {0}, F' = {5},
, где Q' = {0,1,2,3,4,5}, I' = {0}, F' = {5},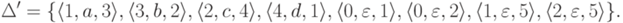
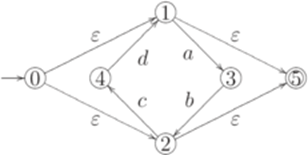
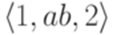 и следующие два перехода заменяют старый переход
и следующие два перехода заменяют старый переход 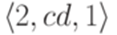 . Чтобы обеспечить единственность начального состояния, добавлены переходы
. Чтобы обеспечить единственность начального состояния, добавлены переходы 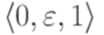 и
и 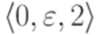 . Последние два перехода в
. Последние два перехода в 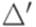 обеспечивают единственность заключительного состояния.
обеспечивают единственность заключительного состояния.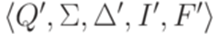 , положив Q' = Q, I' = I,
, положив Q' = Q, I' = I,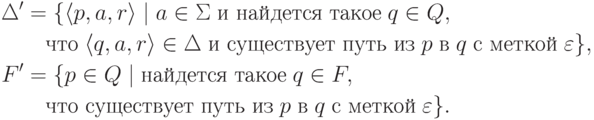
 , I = {1}, F = {3},
, I = {1}, F = {3},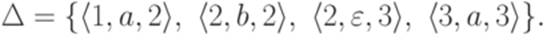

 . Тот же язык распознается конечным автоматом
. Тот же язык распознается конечным автоматом 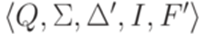 , где F' = {2,3} и
, где F' = {2,3} и