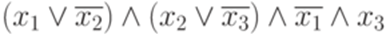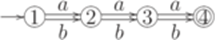Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проблема эквивалентности конечных автоматов
Теорема 15.6.1. Существует алгоритм, позволяющий по произвольным двум праволинейным грамматикам G1 и G2 узнать, верно ли, что Теорема 15.6.2. Существует алгоритм, позволяющий по произвольным двум праволинейным грамматикам G1 и G2 узнать, верно ли, что L(G1) = L(G2). Упражнение 15.6.3. Эквивалентны ли грамматика
и грамматика
15.7*. Проблема эквивалентности детерминированных МП-автоматов Теорема 15.7.1. Существует алгоритм, позволяющий по произвольным двум детерминированным МП-автоматам M1 и M2 узнать, верно ли, что L(M1) = L(M2). Эту теорему доказал Жеро Сенизерг (Geraud Senizergues) в 1997 году. Упрощенное доказательство приводится в [Sti]. Упражнение 15.7.2. Эквивалентны ли два изображенных ниже МП-автомата над алфавитом
Упражнение 15.7.3. Эквивалентны ли два изображенных ниже МП-автомата над алфавитом
15.8*. Классы P и NP Определение 15.8.1. Пусть машина Тьюринга M допускает язык L. Говорят, что язык L распознается за полиномиальное время на машине M, если существует такой многочлен p, что любое слово Определение 15.8.2. Через P обозначается класс тех языков, которые распознаются за полиномиальное время на некоторой детерминированной машине Тьюринга. Определение 15.8.3. Через NP обозначается класс тех формальных языков, которые распознаются за полиномиальное время на некоторой (в общем случае недетерминированной) машине Тьюринга. Замечание 15.8.4. Очевидно, что Теорема 15.8.5. Все языки из класса NP являются разрешимыми. Определение 15.8.6. Всюду определенная функция f из Определение 15.8.7. Язык Определение 15.8.8. Формальный язык L называется NP- сложным (NP-hard}, если каждый язык из класса NPполиномиально сводится к языку L. Определение 15.8.9. Формальный язык называется NP- полным (NP-complete), если он принадлежит классу NP и является NP -сложным.
Определение 15.8.10. Алгоритмическая проблема, относящаяся к некоторой задаче распознавания, называется NP- полной, если множество кодов индивидуальных задач с ответом "да" является NP-полным языком. Теорема 15.8.11 (теорема Кука-Левина). Проблема выполнимости булевых формул в конъюнктивной нормальной форме N- полна. Доказательство можно найти, например, в [Сэв, с. 325-328] или [ГэрДжо, с. 57-63]. Упражнение 15.8.12. Существует ли такой язык Упражнение 15.8.13. Существуют ли такие языки L1 и L2 из класса P, что язык Упражнение 15.8.14. Существуют ли такие языки L1 и L2 из класса NP, что язык 15.9*. Проблема неравенства регулярных выражений без итерации Теорема 15.9.1. Проблема неравенства регулярных выражений без итерации (то есть регулярных выражений с нулевой звездной высотой) NP- полна. Доказательство. По регулярному выражению без итерации легко построить конечный автомат с однобуквенными переходами, не содержащий циклов. Проблема неравенства таких конечных автоматов принадлежит классу NP: достаточно "угадать" слово, принадлежащее разности языков, распознаваемых двумя данными автоматами, и, продвигаясь по этому слову буква за буквой, подобно доказательству теоремы 2.7.1 вычислять, в каких состояниях автоматы могут оказаться. При этом длину слова можно ограничить максимумом числа состояний двух автоматов. Осталось доказать, что проблема неравенства регулярных выражений без итерации NP-сложна. Для этого достаточно продемонстрировать, что к этой проблеме полиномиально сводится проблема выполнимости булевых формул в конъюнктивной нормальной форме (то есть множество кодов выполнимых булевых формул в конъюнктивной нормальной форме полиномиально сводится к множеству кодов пар неравных регулярных выражений без итерации). Искомое полиномиальное сведЕние может быть построено следующим образом. Пусть дана булева формула
Построим два регулярных выражения над алфавитом
Для удобства отождествим истинностные значения "ложь" и "истина" с символами a и b соответственно. Тогда оценку пропозициональных переменных x1, x2,..., xn можно естественным образом отождествить со словом длины n в алфавите
Если m = 1, то это сделать легко. Возьмем в качестве e произведение n сомножителей, каждый из которых совпадает с~одним из следующих четырех регулярных выражений: (a + b), a, b, 0. При этом i -й сомножитель соответствует пропозициональной переменной xi и выбирается следующим образом: · если данная элементарная дизъюнкция не содержит ни литерала xi, ни литерала · если она содержит литерал xi, но не содержит литерала · если она содержит литерал · если она содержит оба литерала xi и Если m > 1, то построим по указанному методу для каждой из булевых формул C1, C2,..., Cm регулярное выражение и возьмем их сумму. Легко видеть, что два построенных так регулярных выражения равны тогда и только тогда, когда булева формула Пример 15.9.2. Пусть (a+b)(a+b)(a+b) и ab(a+b)+(a+b)ab+b(a+b)(a+b)+(a+b)(a+b)a равны, так как булева формула
невыполнима (или, другими словами, булева формула
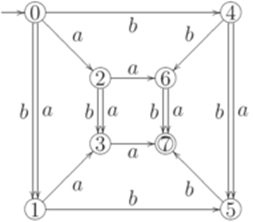
является тавтологией). Упражнение 15.9.3. Равны ли регулярные выражения (a+b)(a+b)(a+b) и bb(a+b)+ba(a+b)+a(a+b)b+(a+b)aa? Упражнение 15.9.4. Равны ли регулярные выражения (a+b)(a+b)(a+b)(a+b) и aab(a+b)+a(a+b)(a+b)b+(a+b)aa(a+b)+(a+b)bb(a+b)+ +(a+b)baa+bab(a+b)+b(a+b)(a+b)b? Упражнение 15.9.5. Эквивалентен ли конечный автомат
конечному автомату, изображенному ниже?
В этой лекции рассматриваются оказавшиеся неразрешимыми алгоритмические проблемы, связанные с контекстно-свободными языками. Всюду предполагается, что в индивидуальных задачах каждый язык представлен контекстно-свободной грамматикой (но можно, конечно, использовать и автоматы с магазинной памятью). В разделе 16.1 доказывается неразрешимость проблемы пустоты пересечения контекстно-свободных языков и проблемы бесконечности пересечения контекстно-свободных языков. В разделе 16.2 доказывается неразрешимость проблемы однозначности контекстно-свободной грамматики. В разделе 16.3 доказывается неразрешимость проблемы равенства контекстно-свободных языков. В разделе 16.4 доказывается неразрешимость проблемы автоматности контекстно-свободного языка. В разделе 16.5 доказывается неразрешимость проблем контекстной свободности дополнения контекстно-свободного языка и пересечения контекстно-свободных языков.
|
||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 89; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.26.20 (0.017 с.) |
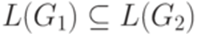 .
.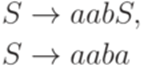
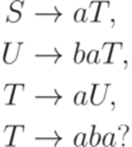
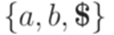 ?
?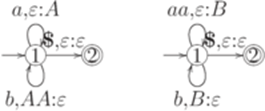
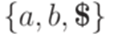 ?
?
 принимается машиной M не более чем за p(|w|) тактов.
принимается машиной M не более чем за p(|w|) тактов. . Неизвестно, совпадают ли классы P и NP.
. Неизвестно, совпадают ли классы P и NP.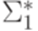 в
в 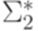 называется вычислимой за полиномиальное время, если ее вычисляет некоторая детерминированная машина Тьюринга M (если
называется вычислимой за полиномиальное время, если ее вычисляет некоторая детерминированная машина Тьюринга M (если 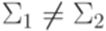 , то данная функция fрассматривается как частичная функция из
, то данная функция fрассматривается как частичная функция из 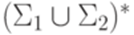 в
в  машина M вычисляет значение f(w) не более чем за p(|w|) тактов.
машина M вычисляет значение f(w) не более чем за p(|w|) тактов. полиномиально сводится (is polynomial time reducible) к языку
полиномиально сводится (is polynomial time reducible) к языку  , если существует такая вычислимая за полиномиальное время всюду определенная функция f из
, если существует такая вычислимая за полиномиальное время всюду определенная функция f из  равносильно условию
равносильно условию 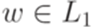 .
.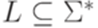 из класса P, что язык
из класса P, что язык  не принадлежит классу P?
не принадлежит классу P? не принадлежит классу P?
не принадлежит классу P?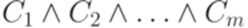 , составленная из пропозициональных переменных x1, x2,..., xn (при более формальном подходе можно считать xi обозначением слова p#i, как это сделано в примере 7.2.8). Здесь для каждого
, составленная из пропозициональных переменных x1, x2,..., xn (при более формальном подходе можно считать xi обозначением слова p#i, как это сделано в примере 7.2.8). Здесь для каждого 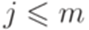 формула Cj является элементарной дизъюнкцией. Для краткости будем обозначать отрицание переменной xi через
формула Cj является элементарной дизъюнкцией. Для краткости будем обозначать отрицание переменной xi через 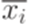 (а не через
(а не через 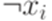 , как в примере 7.2.8).
, как в примере 7.2.8).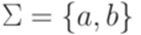 . В качестве первого регулярного выражения возьмем
. В качестве первого регулярного выражения возьмем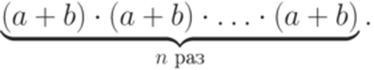
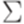 . Второе регулярное выражение e построим так, чтобы выполнялось равенство
. Второе регулярное выражение e построим так, чтобы выполнялось равенство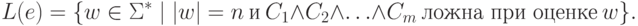
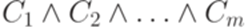 невыполнима.
невыполнима.