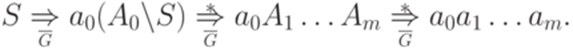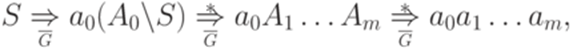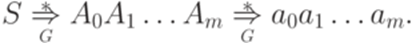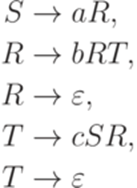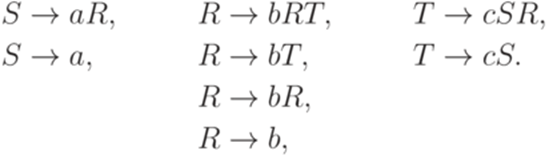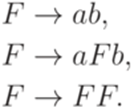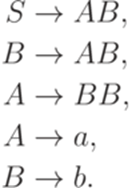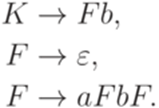Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устранение бесполезных символовСодержание книги
Поиск на нашем сайте
Определение 8.1.1. Пусть дана порождающая грамматика Лемма 8.1.2. Пусть дана контекстно-свободная грамматика Теорема 8.1.3. Пусть дана контекстно-свободная грамматика Доказательство. На первом этапе удалим все непорождающие символы (удалим также каждое правило, содержащее хотя бы один такой символ). На втором этапе из полученной грамматики удалим все недостижимые символы (и правила, их содержащие). Согласно 8.1.2 на втором этапе ни один порождающий символ не может стать непорождающим. Пример 8.1.4. Рассмотрим контекстно-свободную грамматику G с правилами
Удалив четыре правила, содержащие непорождающий символ U, получим грамматику G1. В ней символ X является недостижимым. Удалив три правила, содержащие X, получим грамматику G2 с правилами
Очевидно, что L(G) = L(G2) и грамматика G2 не содержит бесполезных символов. Упражнение 8.1.5. Найти контекстно-свободную грамматику без бесполезных символов, эквивалентную грамматике
Устранение эпсилон-правил Теорема 8.2.1. Пусть язык Доказательство. Пусть дана контекстно-свободная грамматика Если для каких-то Теперь исключим из множества P все правила вида Пример 8.2.2. Рассмотрим язык L, порождаемый грамматикой
Язык
Нормальная форма Хомского Определение 8.3.1. Грамматика в нормальной форме Хомского (грамматика в бинарной нормальной форме, квадратичная грамматика, grammar in Chomsky normal form) - контекстно-свободная грамматика Пример 8.3.2. Грамматика
является грамматикой в нормальной форме Хомского. Теорема 8.3.3. Каждая контекстно-свободная грамматика эквивалентна некоторой грамматике в нормальной форме Хомского. Доказательство. Пусть дана контекстно-свободная грамматика Если правая часть какого-нибудь правила содержит символ S, то заменим грамматику
где S0 - новый символ, не принадлежащий множеству Заменим во всех правилах каждый терминальный символ a на новый нетерминальный символ Ta и добавим к множеству P правила Устраним правила вида Теперь устраним все правила вида Если для каких-то Пример 8.3.4. Грамматика
эквивалентна следующей грамматике в нормальной форме Хомского:
Теорема 8.3.5. Если контекстно-свободный язык не содержит пустого слова, то он порождается некоторой грамматикой, в которой каждое правило имеет один из следующих двух видов:
8.4*. Нормальная форма Грейбах Определение 8.4.1. Грамматика в нормальной форме Грейбах (grammar in Greibach normal form) - контекстно-свободная грамматика Пример 8.4.2. Грамматика
является грамматикой в нормальной форме Грейбах. Замечание 8.4.3. Некоторые авторы разрешают в грамматиках в нормальной форме Грейбах использовать также правила вида Теорема 8.4.4. Каждая контекстно-свободная грамматика эквивалентна некоторой грамматике в нормальной форме Грейбах. Доказательство. Докажем теорему для контекстно-свободных языков, не содержащих пустого слова. Согласно теореме 8.3.5 исходный язык порождается некоторой грамматикой Введем |N|2 новых вспомогательных символов, соответствующих упорядоченным парам из множества
Если в этой грамматике заменить
на
получим эквивалентную ей грамматику в нормальной форме Грейбах. Осталось лишь доказать, что Сначала проверим индукцией по длине слова
где Докажем теперь, что для любого
Теперь убедимся, что
где
Обратно, пусть
где
Пример 8.4.5. Грамматика
эквивалентна следующей грамматике в нормальной форме Грейбах:
Здесь C, D, E и F соответствуют символам (A\S), (A\T), (V\T) и (U\T) из доказательства теоремы 8.4.4 (удален 21 бесполезный символ). Теорема 8.4.6. Пусть язык L контекстно-свободный. Тогда язык Пример 8.4.7. Грамматика
эквивалентна следующей грамматике в нормальной форме Грейбах без
Упражнение 8.4.8. Найти контекстно-свободную грамматику в нормальной форме Грейбах, эквивалентную грамматике
Упражнение 8.4.9. Найти контекстно-свободную грамматику в нормальной форме Грейбах, эквивалентную грамматике
Упражнение 8.4.10. Найти контекстно-свободную грамматику в нормальной форме Грейбах, эквивалентную грамматике
Упражнение 8.4.11. Найти контекстно-свободную грамматику в нормальной форме Грейбах, эквивалентную грамматике
В "лекции 2" были доказаны лемма о разрастании и свойства замкнутости класса автоматных языков. Некоторые из этих теорем имеют аналоги для класса контекстно-свободных языков (разделы 9.1 и 9.4), но этот класс не замкнут относительно дополнения и пересечения (раздел 9.5). Лемма о разрастании для контекстно-свободных языков формализует явление "периодичности" в этих языках. Для полноты картины в разделах 9.2* и 9.3 приведены некоторые аналогичные теоремы для класса линейных языков, хотя ни в теории, ни в практических приложениях класс линейных языков значительной роли не играет. В разделе 9.6 доказывается, что пересечение контекстно-свободного языка с автоматным языком является контекстно-свободным. В сочетании с леммой о разрастании этот факт дает удобное средство, позволяющее во многих задачах доказать, что заданный язык не является контекстно-свободным. Еще одно необходимое условие контекстной свободности сформулировано в разделе 9.7*.
|
||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 397; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.188.174 (0.01 с.) |

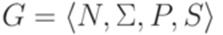 . Символ
. Символ 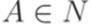 называется полезным (useful), если существуют такие слова
называется полезным (useful), если существуют такие слова 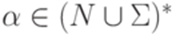 ,
, 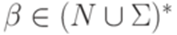 и
и 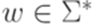 , что
, что 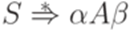 и
и 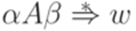 . Символ
. Символ  . Символ
. Символ 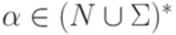 и
и 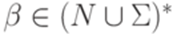 , что
, что 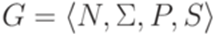 , в которой все символы из N являются порождающими. Пусть N' - множество всех достижимых символов грамматики G, а P' - множество тех правил из P, которые не содержат ни одного символа из множества
, в которой все символы из N являются порождающими. Пусть N' - множество всех достижимых символов грамматики G, а P' - множество тех правил из P, которые не содержат ни одного символа из множества  . Тогда в контекстно-свободной грамматике
. Тогда в контекстно-свободной грамматике 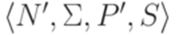 все символы из N' являются порождающими. \end{ lemma }
все символы из N' являются порождающими. \end{ lemma }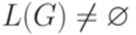 . Тогда существуют такие множества
. Тогда существуют такие множества 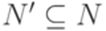 и
и 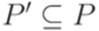 , что в контекстно-свободной грамматике
, что в контекстно-свободной грамматике 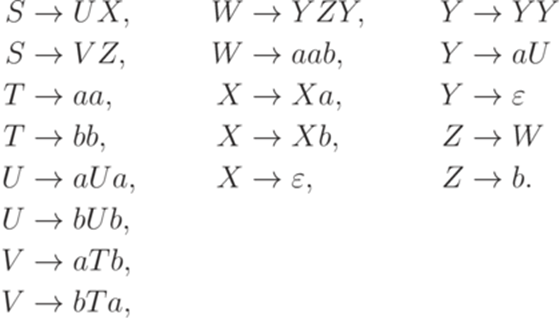
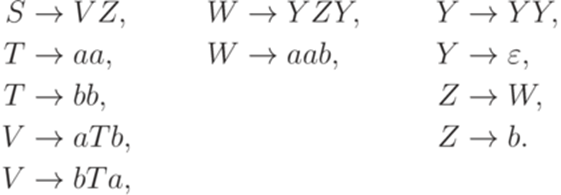
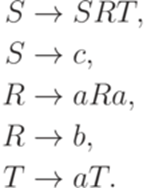
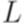 является контекстно-свободным. Тогда язык
является контекстно-свободным. Тогда язык 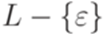 порождается некоторой контекстно-свободной грамматикой без
порождается некоторой контекстно-свободной грамматикой без 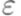 - правил.
- правил.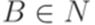 ,
, 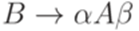 и
и 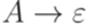 , но не содержит правила
, но не содержит правила  , то добавим это правило в P. Повторяем эту процедуру, пока возможно.
, то добавим это правило в P. Повторяем эту процедуру, пока возможно.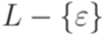 .
.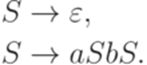
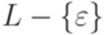 порождается грамматикой
порождается грамматикой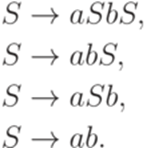
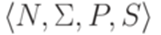 , в которой каждое правило имеет один из следующих трех видов:
, в которой каждое правило имеет один из следующих трех видов: 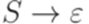 ,
, 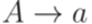 ,
,  , где
, где 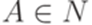 ,
, 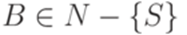 ,
, 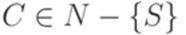 ,
, 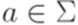 .
.

 .
. для всех
для всех 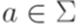 .
.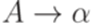 , где
, где  , заменив каждое из них на ряд более коротких правил (при этом добавляются новые нетерминальные символы).
, заменив каждое из них на ряд более коротких правил (при этом добавляются новые нетерминальные символы). и
и  , но не содержит правила
, но не содержит правила  .
.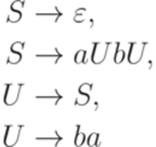
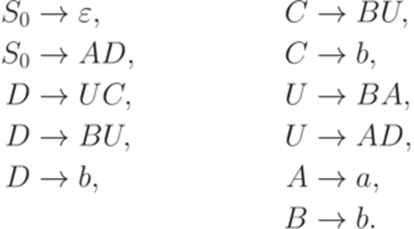
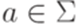 .
.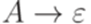 ,
,  ,
, 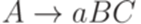 , где
, где 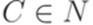 ,
, 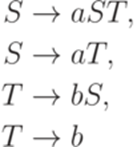
 , где
, где 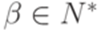 (в определении 8.4.1 разрешены, только если
(в определении 8.4.1 разрешены, только если  ).
).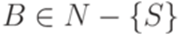 ,
, 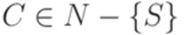 ,
,  . Новый символ, соответствующий паре
. Новый символ, соответствующий паре 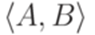 , будем обозначать (A\B). Построим грамматику "почти в нормальной форме Грейбах"
, будем обозначать (A\B). Построим грамматику "почти в нормальной форме Грейбах" 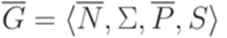 , положив
, положив 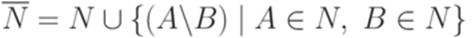 и
и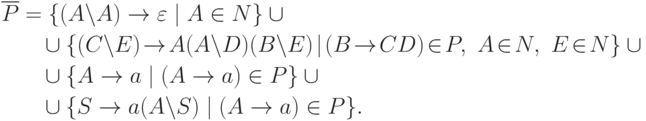
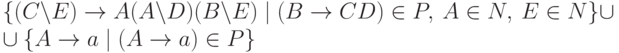
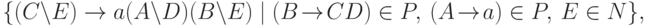
 .
.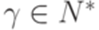 , что если
, что если 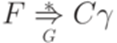 , то
, то 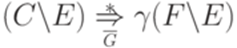 для любого
для любого 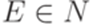 . Чтобы провести шаг индукции, допустим, что
. Чтобы провести шаг индукции, допустим, что  и
и
 и
и 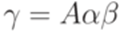 . По предположению индукции имеем
. По предположению индукции имеем 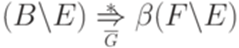 и
и 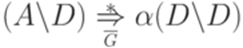 . Подключая эти выводы к правилу
. Подключая эти выводы к правилу  и используя
и используя 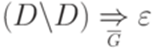 , получаем искомый вывод
, получаем искомый вывод 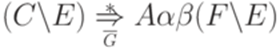 .
.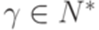 равносильны утверждения
равносильны утверждения 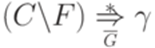 . В одну сторону это следует из только что доказанного. Доказательство того, что если
. В одну сторону это следует из только что доказанного. Доказательство того, что если  ,
,  ,
, 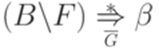 и
и 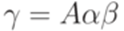 . По предположению индукции
. По предположению индукции  и
и 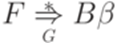 . Получаем искомый вывод
. Получаем искомый вывод
 , где
, где 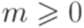 и
и 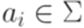 для всех
для всех 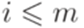 . Пусть
. Пусть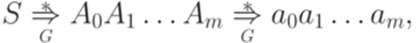
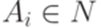 для всех
для всех