
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однозначные контекстно-свободные грамматикиСодержание книги
Поиск на нашем сайте
Определение 7.2.1. Вывод в контекстно-свободной грамматике называется левосторонним (левым, leftmost derivation), если на каждом шаге вывода заменяется самое левое из всех вхождений вспомогательных символов (то есть каждый шаг вывода имеет вид Пример 7.2.2. Вывод
из примера 7.1.2 не является левосторонним. Лемма 7.2.3. Для каждого слова, выводимого в контекстно-свободной грамматике, существует левосторонний вывод. Лемма 7.2.4. Пусть G - контекстно-свободная грамматика над алфавитом Пример 7.2.5. Рассмотрим дерево вывода из примера 7.1.2. Ему соответствует левосторонний вывод
Определение 7.2.6. Контекстно-свободная грамматика называется неоднозначной (ambiguous), если существует слово, которое имеет два или более левосторонних вывода (устаревший термин - неопределенная грамматика). В противном случае контекстно-свободная грамматика называется однозначной (unambiguous). Пример 7.2.7. Контекстно-свободная грамматика из примера 7.1.2 неоднозначна. Слово ababab имеет два левосторонних вывода:
и
Пример 7.2.8. Пусть
порождает множество всех булевых формул, составленных из переменных p, p#, p##,..., с помощью скобок и операторов Определение 7.2.9. Контекстно-свободный язык называется существенно неоднозначным (inherently ambiguous), если каждая контекстно-свободная грамматика, порождающая этот язык, является неоднозначной. Пример 7.2.10. Язык, порождаемый контекстно-свободной грамматикой из примера 7.1.2, не является существенно неоднозначным. Он порождается однозначной грамматикой
Пример 7.2.11. Пусть 7.3*. Однозначные праволинейные грамматики Теорема 7.3.1. Каждый праволинейный язык порождается некоторой однозначной праволинейной грамматикой. Другими словами, ни один праволинейный язык не является существенно неоднозначным. Доказательство. Согласно теоремам 2.4.3 и 2.7.1 исходный язык распознается некоторым детерминированным конечным автоматом. Применив к нему конструкцию из доказательства теоремы 2.4.1, получим однозначную праволинейную грамматику. Замечание 7.3.2. Этот факт можно получить также из более общей теоремы 12.2.6 с учетом теоремы 12.2.1. Упражнение 7.3.3. Найти однозначную праволинейную грамматику, порождающую язык a*((a+b)(a+b))*b*. Языки Дика и Лукасевича Определение 7.4.1. Языком Дика (Dyck language) над 2n буквами называется контекстно-свободный язык над алфавитом {a1,b1,a2,b2,...,an,bn}, порождаемый грамматикой
Замечание 7.4.2. Словами этого языка являются последовательности правильно вложенных скобок n типов (если считать символ ai левой скобкой, а символ bi соответствующей правой скобкой). Теорема 7.4.3. Слово w над алфавитом {a,b} выводится в грамматике
тогда и только тогда, когда
и для всех слов
Теорема 7.4.4. При любом положительном целом n грамматика из определения 7.4.1 является однозначной. Определение 7.4.5. Языком Лукасевича (Lukasiewicz language) над n + 1 буквами называется контекстно-свободный язык над алфавитом {a0,a1,...,an}, порождаемый грамматикой
Теорема 7.4.6. Слово w над алфавитом {a0,a1,...,an} принадлежит языку Лукасевича над n + 1 буквами тогда и только тогда, когда
и для всех слов
Теорема 7.4.7. При любом Основная цель этой лекции - доказать, что каждая контекстно-свободная грамматика эквивалентна некоторой контекстно-свободной грамматике специального вида, а именно грамматике в нормальной форме Хомского (раздел 8.3). Этот факт используется дальше в доказательствах многих теорем о контекстно-свободных языках. Два вспомогательных результата, на которые опирается приведение грамматик к нормальной форме Хомского, выделены в отдельные разделы в начале лекции. В конце лекции доказывается, что каждую контекстно-свободную грамматику можно также привести к нормальной форме Грейбах.
|
||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.36 (0.006 с.) |

 , где
, где 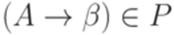 ,
, 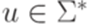 и
и 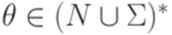 ). Иногда в левосторонних выводах вместо
). Иногда в левосторонних выводах вместо 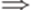 пишут \lmarrow. Правосторонний (правый) вывод определяется аналогично. В правосторонних выводах вместо
пишут \lmarrow. Правосторонний (правый) вывод определяется аналогично. В правосторонних выводах вместо 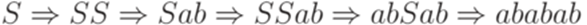
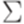 . Пусть
. Пусть 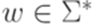 . Тогда существует взаимно-однозначное соответствие между левосторонними выводами слова w в грамматике G и деревьями вывода в грамматике G, кроной которых является w.
. Тогда существует взаимно-однозначное соответствие между левосторонними выводами слова w в грамматике G и деревьями вывода в грамматике G, кроной которых является w.


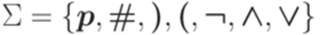 . Контекстно-свободная грамматика
. Контекстно-свободная грамматика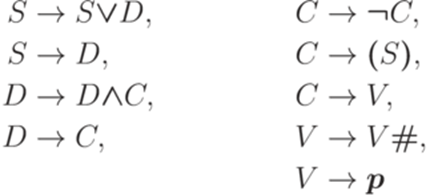
 ,
,  и
и  . Эта грамматика является однозначной.
. Эта грамматика является однозначной.
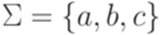 . Контекстно-свободный язык {akbmcn | k = m или m = n} является существенно неоднозначным. Доказательство этого факта можно найти в [АхоУль, с. 234-236].
. Контекстно-свободный язык {akbmcn | k = m или m = n} является существенно неоднозначным. Доказательство этого факта можно найти в [АхоУль, с. 234-236].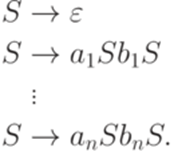
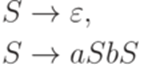

 выполняется неравенство
выполняется неравенство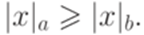
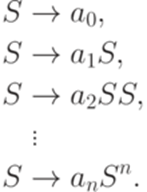
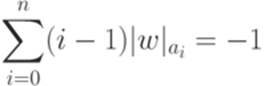
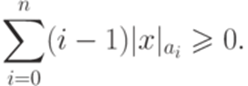
 грамматика из определения 7.4.5 является однозначной.
грамматика из определения 7.4.5 является однозначной.


