
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пересечение контекстно-свободного языка с автоматным языком
Теорема 9.6.1. Если L1 - контекстно-свободный язык и L2 - автоматный язык, то язык Доказательство. Пусть Построим контекстно-свободную грамматику
где Пример 9.6.2. Пусть
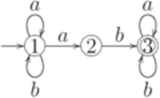
и автоматный язык L2, распознаваемый конечным автоматом
Тогда язык
Здесь S11, S12, S21 и S22 соответствуют символам Теорема 9.6.3*. Если L1 - линейный язык и L2 - автоматный язык, то язык Пример 9.6.4*. Пусть
и автоматный язык L2, распознаваемый конечным автоматом
Тогда язык
Эту грамматику можно упростить, заменив S11 и S33 на один символ. Упражнение 9.6.5. Найти контекстно-свободную грамматику для языка
а язык L2 порождается грамматикой
Упражнение 9.6.6. Найти контекстно-свободную грамматику для языка
а язык L2 порождается грамматикой
Упражнение 9.6.7. Является ли контекстно-свободным язык Упражнение 9.6.8. Является ли контекстно-свободным язык Упражнение 9.6.9. Существует ли над алфавитом {a,b} такой линейный язык L, что язык 9.7*. Теорема Парика Замечание 9.1.7. В этом разделе предполагается, что зафиксирован некоторый линейный порядок на алфавите Определение 9.7.2. Через
Пример 9.7.3. Пусть Определение 9.7.4. Пусть
При этом множество B называется системой предпериодов множества L(B,P). Множество P называется системой периодов множества L(B,P).
Определение 9.7.5. Множество Определение 9.7.6. Множество Теорема 9.7.7 (Теорема Парика). Если язык Доказательство можно найти в [Гин, с. 207-211]. Пример 9.7.8. Пусть Теорема 9.7.9. Если множество Доказательство. Докажем это для произвольного линейного множества A = L(B,P) (на полулинейные множества утверждение распространяется по теореме 3.1.1). Рассмотрим конечный автомат
Очевидно, что Замечание 9.7.10. Теорема 9.3.1 является следствием теорем 9.7.7 и 9.7.9. Упражнение 9.7.11. Является ли контекстно-свободным язык Подобно тому, как праволинейным грамматикам соответствуют конечные автоматы, контекстно-свободным грамматикам соответствуют автоматы с магазинной памятью (МП-автоматы). В таком автомате, помимо ограниченной памяти, хранящей текущее состояние, имеется потенциально бесконечная память, используемая как стек (магазин), то есть структура данных, где в каждый момент доступен только тот элемент, который был добавлен позже остальных присутствующих на данный момент элементов. Для наглядности стек обычно изображают вертикально, так, что доступный элемент данных (вершина) находится наверху. Но при формальном определении конфигурации (мгновенного состояния) МП-автомата удобно считать все содержимое стека конечной последовательностью символов, то есть словом (в алфавите, в котором перечислены все возможные данные, "умещающиеся" в одной ячейке стека). Прежде чем определить конфигурацию, придется принять произвольное соглашение о том, в каком порядке записывать содержимое стека в этом слове. В этой книге считается, что вершина стека находится в начале слова (то есть слева). В разделе 10.1 даются необходимые определения. В разделе 10.2 доказывается, что МП-автоматы распознают в точности контекстно-свободные языки.
|
||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.97.248 (0.006 с.) |
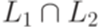 является контекстно-свободным.
является контекстно-свободным.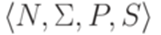 - контекстно-свободная грамматика, порождающая язык L1. Без ограничения общности можно считать, что множество P содержит только правила вида
- контекстно-свободная грамматика, порождающая язык L1. Без ограничения общности можно считать, что множество P содержит только правила вида 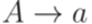 и
и 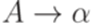 , где
, где 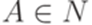 ,
, 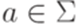 и
и 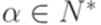 (см. теорему 8.3.3). Пусть
(см. теорему 8.3.3). Пусть  - конечный автомат, распознающий язык L_2. Без ограничения общности можно считать, что для каждого перехода
- конечный автомат, распознающий язык L_2. Без ограничения общности можно считать, что для каждого перехода 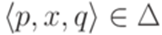 выполняется равенство |x| = 1(см. лемму 2.3.3).
выполняется равенство |x| = 1(см. лемму 2.3.3).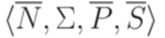 , порождающую язык
, порождающую язык 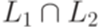 . Положим
. Положим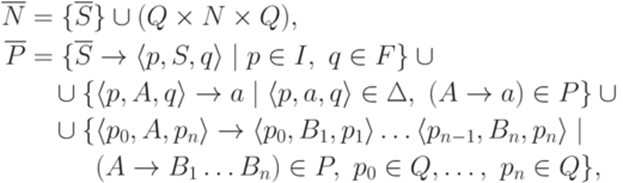
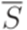 - новый символ (не принадлежащий множеству
- новый символ (не принадлежащий множеству 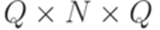 ).
).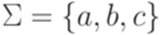 . Рассмотрим контекстно-свободный язык L1, порождаемый грамматикой
. Рассмотрим контекстно-свободный язык L1, порождаемый грамматикой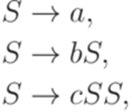
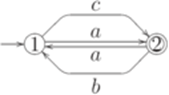
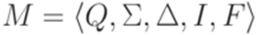 , где Q = {1,2}, I = {1}, F = {2},
, где Q = {1,2}, I = {1}, F = {2},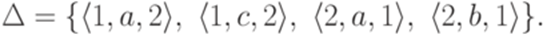
 порождается контекстно-свободной грамматикой
порождается контекстно-свободной грамматикой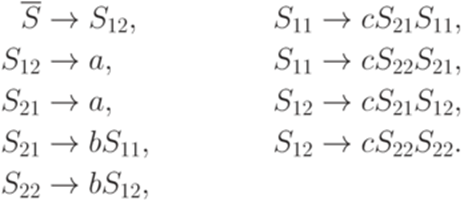
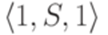 ,
, 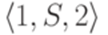 ,
, 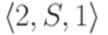 и
и 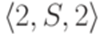 из доказательства теоремы 9.6.1.
из доказательства теоремы 9.6.1.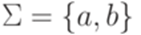 . Рассмотрим линейный язык L1, порождаемый грамматикой
. Рассмотрим линейный язык L1, порождаемый грамматикой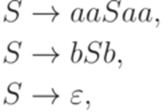
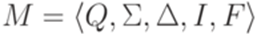 , где Q = {1,2,3}, I = {1}, F = {3},
, где Q = {1,2,3}, I = {1}, F = {3},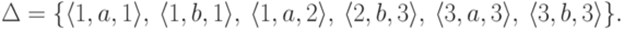
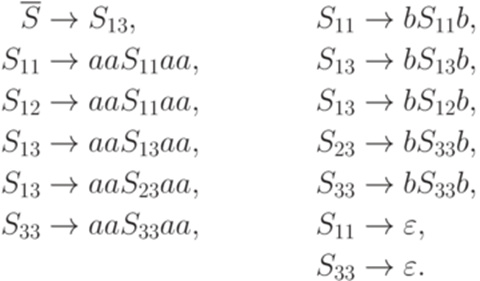
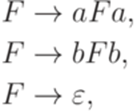


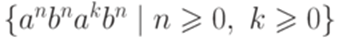
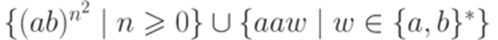
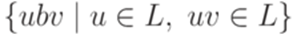 не является контекстно-свободным?
не является контекстно-свободным? . Пусть
. Пусть 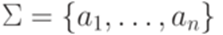 .
.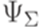 будем обозначать функцию из
будем обозначать функцию из 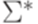 в
в  , определенную следующим образом:
, определенную следующим образом: 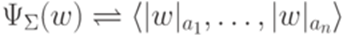 . Аналогично, каждому языку
. Аналогично, каждому языку 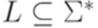 ставится в соответствие множество
ставится в соответствие множество 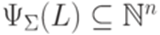 , определенное следующим образом:
, определенное следующим образом: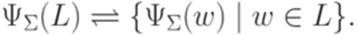
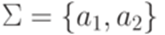 и L = {a1,a1a2a2,a2a2a1}. Тогда
и L = {a1,a1a2a2,a2a2a1}. Тогда 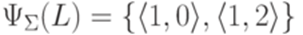 .
.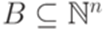 и
и 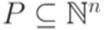 . Тогда через
. Тогда через 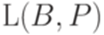 обозначается множество
обозначается множество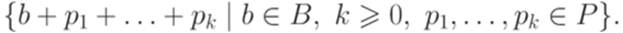
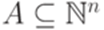 называется линейным (linear), если A = L(B,P) для некоторых конечных множеств B и P.
называется линейным (linear), если A = L(B,P) для некоторых конечных множеств B и P.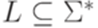 является контекстно-свободным, то множество
является контекстно-свободным, то множество 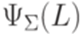 является полулинейным.
является полулинейным.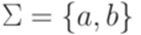 . Рассмотрим язык
. Рассмотрим язык 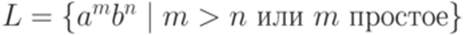 . Можно проверить, что множество
. Можно проверить, что множество 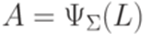 .
.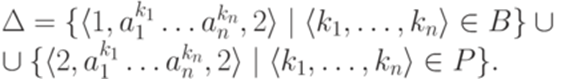
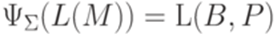 .
.



