
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства замкнутости класса линейных языков
Пример 9.3.1. Пусть
Пример 9.3.2. Рассмотрим алфавит
является линейным, так как он порождается грамматикой
Теорема 9.3.3. Если L1 и L2 - линейные языки над алфавитом Доказательство. Пусть язык L1 порождается линейной грамматикой
где Пример 9.3.4. Рассмотрим алфавит
является линейным, поскольку
где языки
являются линейными, а язык
является автоматным, и можно применить теоремы 9.3.3, 3.2.1, 2.4.1 и лемму 1.5.13. Упражнение 9.3.5. Пусть Упражнение 9.3.6. Пусть Упражнение 9.3.7. Найти линейную грамматику, порождающую язык
Свойства замкнутости класса контекстно-свободных языков Теорема 9.4.1. Если L - контекстно-свободный язык, то L* тоже контекстно-свободный язык. Доказательство. Пусть язык L порождается контекстно-свободной грамматикой
где Теорема 9.4.2. Если L1 и L2 - контекстно-свободные языки над алфавитом Доказательство. Пусть язык L1 порождается контекстно-свободной грамматикой
где Теорема 9.4.3. Если L1 и L2 - контекстно-свободные языки над алфавитом Доказательство. Пусть язык L1 порождается контекстно-свободной грамматикой
где Теорема 9.4.4. Если L - контекстно-свободный язык, то Упражнение 9.4.5. Является ли контекстно-свободным язык Упражнение 9.4.6. Найти контекстно-свободную грамматику для языка
а язык L2 порождается грамматикой
Пересечение и дополнение контекстно-свободных языков Теорема 9.5.1. Неверно, что для любых контекстно-свободных языков L1 и L2 язык Доказательство. Положим Теорема 9.5.2. Неверно, что для любого контекстно-свободного языка
Доказательство. Положим Упражнение 9.5.3. Является ли контекстно-свободным язык Упражнение 9.5.4. Является ли контекстно-свободным язык Упражнение 9.5.5. Существует ли такой линейный язык L над алфавитом {a,b}, что язык
|
|||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 95; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.240.142 (0.008 с.) |
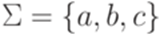 . Язык
. Язык  является линейным, так как он порождается грамматикой
является линейным, так как он порождается грамматикой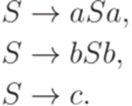
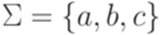 . Язык
. Язык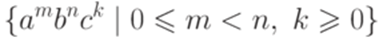

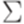 , то
, то 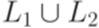 тоже линейный язык.
тоже линейный язык.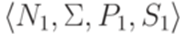 и L2 порождается линейной грамматикой
и L2 порождается линейной грамматикой 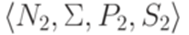 , где
, где 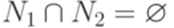 . Тогда
. Тогда  порождается грамматикой
порождается грамматикой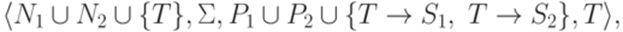
 .
.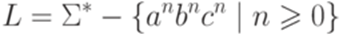
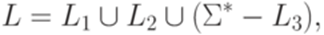
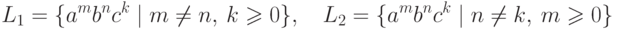

 ?
?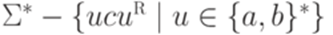 ?
? , где L1 порождается грамматикой
, где L1 порождается грамматикой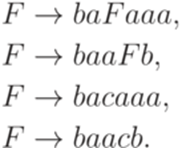
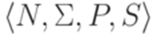 . Тогда язык L*порождается грамматикой
. Тогда язык L*порождается грамматикой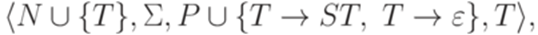
 .
. , то
, то  тоже контекстно-свободный язык.
тоже контекстно-свободный язык. и L2 порождается контекстно-свободной грамматикой
и L2 порождается контекстно-свободной грамматикой  , где
, где  порождается грамматикой
порождается грамматикой
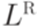 тоже контекстно-свободный язык.
тоже контекстно-свободный язык. ?
?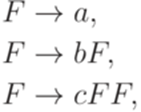

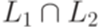 тоже контекстно-свободный.
тоже контекстно-свободный.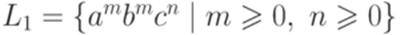 и
и 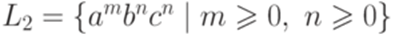 . В примере 9.2.1 было доказано, что язык
. В примере 9.2.1 было доказано, что язык 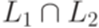 не является контекстно-свободным.
не является контекстно-свободным.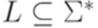 язык
язык  тоже контекстно-свободный.
тоже контекстно-свободный.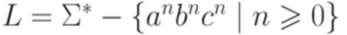 , где
, где 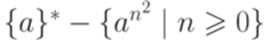 ?
? ?
? не является контекстно-свободным?
не является контекстно-свободным?


