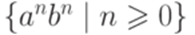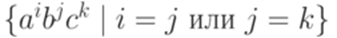Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение автомата с магазинной памятьюСодержание книги
Поиск на нашем сайте
Определение 10.1.1. Автомат с магазинной памятью (МП-автомат, магазинный автомат, стековый автомат, pushdown automaton) - это шестерка
Здесь Q - множество состояний, Пример 10.1.2. Пусть Q = {1,2},
Замечание 10.1.3. МП-автоматы можно изображать в виде диаграмм состояний. На диаграмме каждое состояние обозначается кружком, а переход - стрелкой. Каждое начальное состояние распознается по ведущей в него короткой стрелке. Каждое допускающее состояние отмечается на диаграмме двойным кружком. Стрелка с пометкой Пример 10.1.4. Ниже приведена диаграмма МП-автомата из примера 10.1.2.
Определение 10.1.5. Конфигурацией МП-автомата называется любая тройка Определение 10.1.6. Определим на множестве всех конфигураций МП-автомата Замечание 10.1.7 Обычно из контекста ясно, о каком МП-автомате идет речь. Тогда вместо Пример 10.1.8. Для МП-автомата из примера 10.1.2 выполняется Определение 10.1.9. Бинарное отношение Пример 10.1.10. Для МП-автомата из примера 10.1.2 выполняется Лемма 10.1.11. Если Доказательство. Лемму легко доказать индукцией по количеству тактов в вычислительном процессе, ведущем из конфигурации Определение 10.1.12. Слово Определение 10.1.13. Язык, распознаваемый МП-автоматом, - множество всех слов, допускаемых этим МП-автоматом. Язык, распознаваемый МП-автоматом M, обозначается L(M). Замечание 10.1.14. Обычно в учебниках используется более узкое определение МП-автомата, но это не меняет класса языков, распознаваемых МП-автоматами. Пример 10.1.15. Пусть Пример 10.1.16. Пусть
Тогда Определение 10.1.17. Два МП-автомата эквивалентны, если они распознают один и тот же язык. Замечание 10.1.18. В данном пособии не рассматриваются преобразователи с магазинной памятью (pushdown transducer) обобщение автоматов с магазинной памятью посредством добавления "выходного" потока (см. [7, 3.5] или [2, 3.1.4]). Замечание 10.1.19. Некоторые авторы изменяют определение допускаемых слов следующим образом: слово w допускается МП-автоматом Замечание 10.1.20. Некоторые авторы добавляют в определение МП-автомата седьмую компоненту - Z0, называемую маркером магазинной памяти (start pushdown symbol), и изменяют определение допускаемых слов следующим образом: слово w допускается МП-автоматом Замечание 10.1.21. Класс языков, распознаваемых МП-автоматами, не изменится также, если использовать следующую естественную комбинацию двух предыдущих определений: слово w допускается МП-автоматом Замечание 10.1.22. Некоторые авторы добавляют в определение МП-автомата маркер магазинной памяти Z0, отбрасывают множество F и изменяют определение допускаемых слов следующим образом: слово w допускается МП-автоматом Упражнение 10.1.23. Найти МП-автомат, распознающий язык Упражнение 10.1.24. Найти МП-автомат, распознающий язык Упражнение 10.1.25. Найти МП-автомат, распознающий язык
|
||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.218.44 (0.007 с.) |

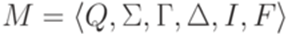 , где
, где  ,
, 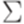 ,
, 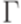 и
и  - конечные множества,
- конечные множества, 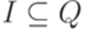 ,
, 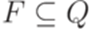 и
и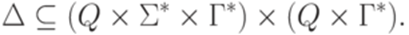
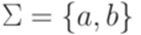 ,
,  ,
,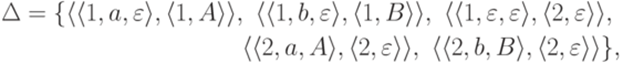
 ,
,  . Тогда
. Тогда 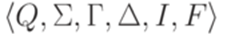 - МП-автомат.
- МП-автомат.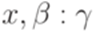 , ведущая из p в q, показывает, что
, ведущая из p в q, показывает, что 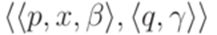 является переходом данного МП-автомата.
является переходом данного МП-автомата.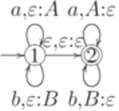
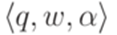 , где
, где  ,
, 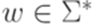 ,
, 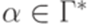 .
.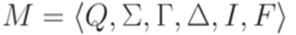 бинарное отношение
бинарное отношение 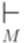 (такт работы) следующим образом. Если
(такт работы) следующим образом. Если 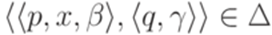 ,
, 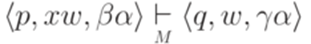 .
.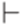 .
. и
и 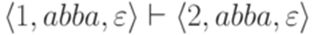 .
.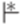 определяется как рефлексивное, транзитивное замыкание отношения
определяется как рефлексивное, транзитивное замыкание отношения 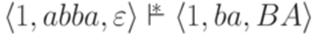 и
и 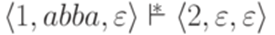 .
. и
и 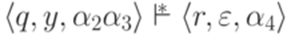 , то
, то 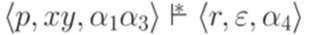 .
.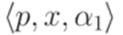 в конфигурацию
в конфигурацию 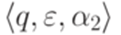 .
.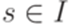 и
и 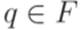 , что
, что 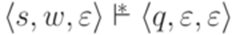 .
.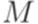 - МП-автомат из примера 10.1.2. Тогда
- МП-автомат из примера 10.1.2. Тогда 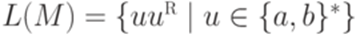 .
.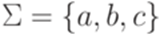 . Рассмотрим МП-автомат
. Рассмотрим МП-автомат 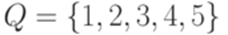 ,
,  , I = {1}, F = {4,5} и
, I = {1}, F = {4,5} и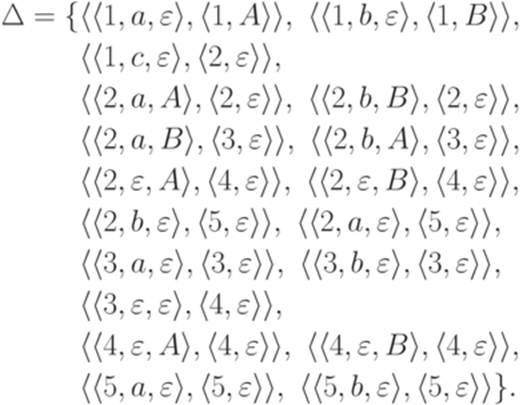
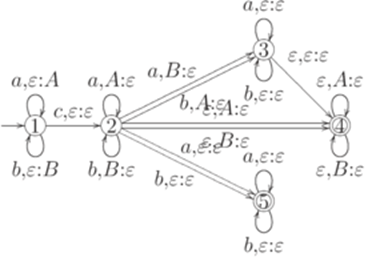
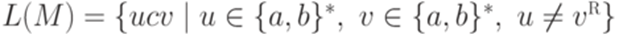 .
.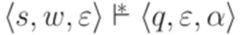 . Такое определение не изменяет класса языков, распознаваемых МП-автоматами.
. Такое определение не изменяет класса языков, распознаваемых МП-автоматами. , если найдутся такие состояния
, если найдутся такие состояния 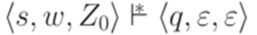 . Такое определение не изменяет класса языков, распознаваемых МП-автоматами.
. Такое определение не изменяет класса языков, распознаваемых МП-автоматами. , если найдутся такие состояния
, если найдутся такие состояния 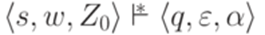 .
.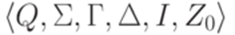 , если найдутся такие состояния
, если найдутся такие состояния 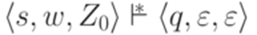 . Это также не изменяет класса языков, распознаваемых МП-автоматами.
. Это также не изменяет класса языков, распознаваемых МП-автоматами.