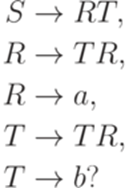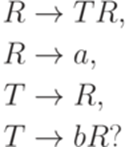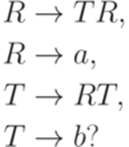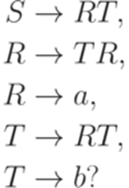Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дополнение контекстно-свободного языкаСодержание книги
Поиск на нашем сайте Лемма 16.3.1. Рассмотрим алфавит Пример 16.3.2. Пусть
Заметим, что Язык Замечание 16.3.3. Лемму 16.3.1 можно доказать, явно построив контекстно-свободную грамматику (как в примере 16.3.2), а можно и вывести из теоремы 12.2.7}, проверив, что Определение 16.3.4. Пусть Лемма 16.3.5. Язык Доказательство. Лемма 16.3.6. Дополнение языка Доказательство Утверждение следует из леммы 16.1.2. Теорема 16.3.7. Пусть Доказательство Очевидно, что Теорема 16.3.8. Пусть Доказательство Утверждение следует из предыдущей теоремы и примера 1.5.16. Теорема 16.3.9. Пусть Доказательство Очевидно, что Лемма 16.3.10. Дополнение языка Теорема 16.3.11. Пусть Упражнение 16.3.12. Рассмотрим язык, порождаемый грамматикой
Содержит ли этот язык все слова из {a,b}*? Упражнение 16.3.13. Рассмотрим язык, порождаемый грамматикой
{a,b}*? Проблема автоматности Лемма 16.4.1. Пусть Доказательство Пусть
Легко проверить, что
Как было установлено в упражнении 3.4.2, язык Обратно, если постовская система соответствия Теорема 16.4.2. Пусть Доказательство Докажем утверждение теоремы для случая Упражнение 16.4.3. Является ли автоматным язык, порождаемый грамматикой
Упражнение 16.4.4. Является ли автоматным язык, порождаемый грамматикой
Упражнение 16.4.5. Является ли автоматным язык, порождаемый грамматикой
Упражнение 16.4.6. Является ли автоматным язык, порождаемый грамматикой
|
||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 . Язык
. Язык  является контекстно-свободным при любом
является контекстно-свободным при любом 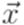 .
.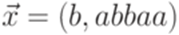 . Тогда язык
. Тогда язык 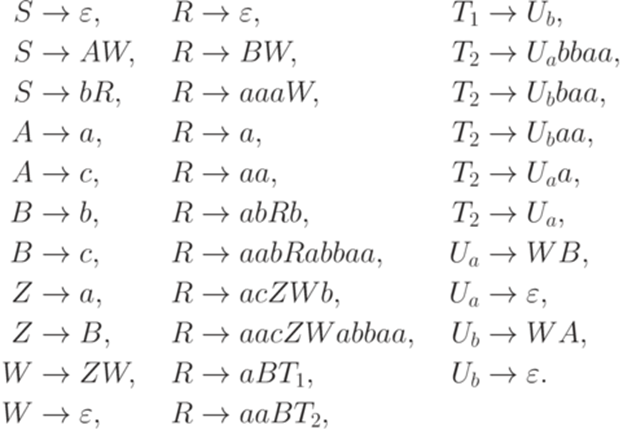
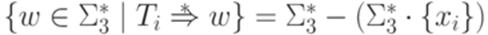 для каждого i.
для каждого i.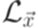 - детерминированный контекстно-свободный язык.
- детерминированный контекстно-свободный язык.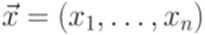 ,
, 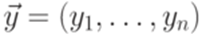 , где
, где 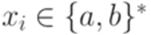 и
и 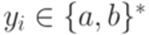 для всех i. Обозначим через
для всех i. Обозначим через  язык
язык 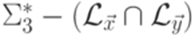 .
.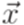 и
и 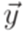 .
.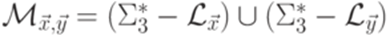 .
.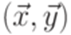 имеет решение.
имеет решение. . Тогда не существует алгоритма, позволяющего по произвольной контекстно-свободной грамматике G над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольной контекстно-свободной грамматике G над алфавитом 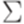 узнать, верно ли, что
узнать, верно ли, что  .
.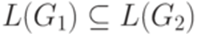 .
.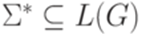 тогда и только тогда, когда
тогда и только тогда, когда  .
.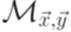 является бесконечным тогда и только тогда, когда постовская система соответствия
является бесконечным тогда и только тогда, когда постовская система соответствия 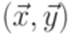 имеет решение.
имеет решение. . Тогда не существует алгоритма, позволяющего по произвольной контекстно-свободной грамматике G над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольной контекстно-свободной грамматике G над алфавитом 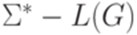 .
.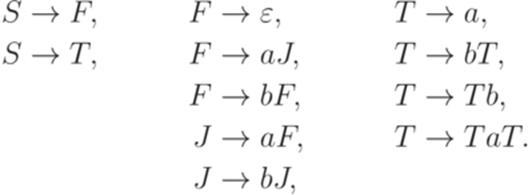
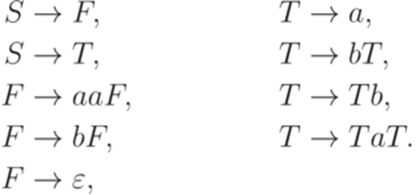
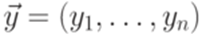 , где
, где 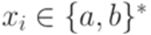 ,
, 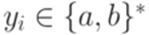 и
и 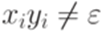 для всех i. Тогда язык
для всех i. Тогда язык  является автоматным в том и только том случае, когда постовская система соответствия
является автоматным в том и только том случае, когда постовская система соответствия 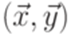 не имеет решений.
не имеет решений.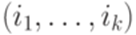 - решение постовской системы соответствия
- решение постовской системы соответствия 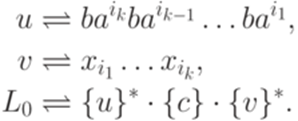
 ,
,  и язык L0 является автоматным. Очевидно, что
и язык L0 является автоматным. Очевидно, что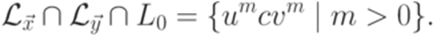
 не является автоматным. Согласно теореме 3.2.1 язык
не является автоматным. Согласно теореме 3.2.1 язык 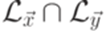 не является автоматным. Следовательно, и язык
не является автоматным. Следовательно, и язык 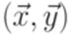 не имеет решений, то
не имеет решений, то 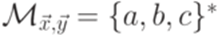 , а этот язык является автоматным.
, а этот язык является автоматным. . Из леммы 16.4.1 следует, что если бы проблема распознавания автоматности языка L(G) для контекстно-свободных грамматик над алфавитом
. Из леммы 16.4.1 следует, что если бы проблема распознавания автоматности языка L(G) для контекстно-свободных грамматик над алфавитом 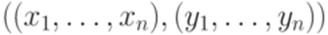 , где
, где 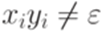 для всех i. Но тогда была бы разрешима проблема соответствий Поста для всех постовских систем соответствия над алфавитом {a,b} (если
для всех i. Но тогда была бы разрешима проблема соответствий Поста для всех постовских систем соответствия над алфавитом {a,b} (если 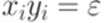 для некоторого i, то рассматриваемая постовская система соответствия имеет решение, а именно (i)).
для некоторого i, то рассматриваемая постовская система соответствия имеет решение, а именно (i)).