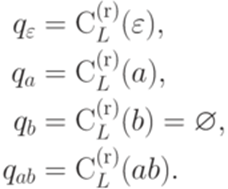Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Недетерминированные конечные автоматыСтр 1 из 21Следующая ⇒
Формальные языки Определение 1.1.1. Будем называть натуральными числами неотрицательные целые числа. Множество всех натуральных чисел {0, 1, 2,...} обозначается N. Определение 1.1.2. Алфавитом называется конечное непустое множество. Его элементы называются символами (буквами). Определение 1.1.3. Словом (цепочкой, строкой, string) в алфавите Пример 1.1.4. Рассмотрим алфавит Определение 1.1.5. Слово, не содержащее ни одного символа (то есть последовательность длины 0), называется пустым словом и обозначается Определение 1.1.6. Множество всех слов в алфавите Замечание 1.1.7. Множество Определение 1.1.8. Множество всех непустых слов в алфавите Пример 1.1.9. Если Определение 1.1.10. Если Поскольку каждый язык является множеством, можно рассматривать операции объединения, пересечения и разности языков, заданных над одним и тем же алфавитом (обозначения Пример 1.1.11. Множество {a, abb} является языком над алфавитом {a, b}. Определение 1.1.12. Пусть Определение 1.1.13. Если x и y - слова в алфавите Определение 1.1.14. Если x - слово и Пример 1.1.15. По принятым соглашениям ba3 = baaa и (ba)3 = bababa. Пример 1.1.16. Множество Определение 1.1.17. Длина слова w, обозначаемая |w|, есть число символов в w, причем каждый символ считается столько раз, сколько раз он встречается в w.
Пример 1.1.18. Очевидно, что |baaa| = 4 и Определение 1.1.19. Через |w|a обозначается количество вхождений символа a в слово w. Пример 1.1.20. Если Операции над языками Определение 1.2.1. Пусть
Язык Пример 1.2.2. Если L1 = {a,abb} и L2 = {bbc,c}, то Определение 1.2.4. Пусть
Пример 1.2.5. Если L = {akbal | 0 < k < l}, то L2 = {akbalbam | 0 < k < l - 1, m > 1}. Определение 1.2.7. Итерацией языка (Kleene closure) языка L (обозначение L*) называется язык
Эта операция называется также звездочкой Клини (Kleene star, star operation). Пример 1.2.8. Если
Определение 1.2.11. Обращением или зеркальным образом слова w (обозначается wR) называется слово, в котором символы, составляющие слово w, идут в обратном порядке. Пример 1.2.12. Если w = baaca, то wR = acaab. Определение 1.2.13. Пусть
Язык LR называется обращением языка L. Определение 1.2.15. Говорят, что слово x - префикс (начало) слова y (обозначение Пример 1.2.16. Очевидно, что Определение 1.2.17. Пусть
Множество Pref(L) называется множеством префиксов языка L. Определение 1.2.18 Говорят, что слово x - суффикс (конец) слова y (обозначение Определение 1.2.19. Пусть
Множество Suf(L) называется множеством суффиксов языка L. Определение 1.2.20. Говорят, что слово x - подслово (substring) слова y, если y = uxv для некоторых слов u и v. Определение 1.2.21. Пусть Определение 1.2.22. Слово a1a2...an (длины Замечание 1.2.23. Все подслова слова y являются также подпоследовательностями слова y. Определение 1.2.24. Пусть
Пример 1.2.25. Рассмотрим язык L = { cba, c} над алфавитом {a, b, c}. Очевидно, что Определение 1.2.26. Функция Определение 1.2.27. Множества K и L называются равномощными (of equal cardinality), если существует биекция из K в L. Гомоморфизмы Определение 1.3.1. Пусть Замечание 1.3.2. Можно доказать, что если Замечание 1.3.3. Пусть Замечание 1.3.4. Каждый гомоморфизм однозначно определяется своими значениями на однобуквенных словах. Замечание 1.3.5. Если Пример 1.3.6. Пусть
Определение 1.3.7. Если Пример 1.3.8. Рассмотрим алфавит
Порождающие грамматики Определение 1.4.1. Порождающей грамматикой (грамматикой типа 0, generative grammar, rewrite grammar) называется четверка Пример 1.4.2. Пусть даны множества N = {S}, Замечание 1.4.3. Будем обозначать элементы множества Замечание 1.4.4. Для обозначения n правил с одинаковыми левыми частями Определение 1.4.5. Пусть дана грамматика G. Пишем Замечание 1.4.6. Когда из контекста ясно, о какой грамматике идет речь, вместо Пример 1.4.7. Пусть
Тогда Определение 1.4.8. Если При этом последовательность слов Замечание 1.4.9. В частности, для всякого слова Пример 1.4.10. Пусть Определение 1.4.11. Язык, порождаемый грамматикой G, - это множество
Замечание 1.4.12. Существенно, что в определение порождающей грамматики включены два алфавита - Пример 1.4.13. Если Определение 1.4.14. Две грамматики эквивалентны, если они порождают один и тот же язык. Пример 1.4.15. Грамматика
и грамматика
эквивалентны. Классы грамматик Определение 1.5.1. Контекстной грамматикой (контекстно-зависимой грамматикой, грамматикой непосредственно составляющих, НС-грамматикой, грамматикой типа 1, context-sensitive grammar, phrase-structure grammar) называется порождающая грамматика, каждое правило которой имеет вид Пример 1.5.2. Грамматика
не является контекстной (последние три правила не имеют требуемого вида). Определение 1.5.3. Контекстно-свободной грамматикой (бесконтекстной грамматикой, КС-грамматикой, грамматикой типа 2, context-free grammar) называется порождающая грамматика, каждое правило которой имеет вид Пример 1.5.4. Грамматика
является контекстной, но не контекстно-свободной (последние пять правил не имеют требуемого вида). Определение 1.5.5. Линейной грамматикой (linear grammar) называется порождающая грамматика, каждое правило которой имеет вид Грамматика
является контекстно-свободной, но не линейной (первые два правила не имеют требуемого вида). Определение 1.5.7. Праволинейной грамматикой (рациональной грамматикой, грамматикой типа 3, right-linear grammar) называется порождающая грамматика, каждое правило которой имеет вид Пример 1.5.8. Грамматика
является линейной, но не праволинейной (первое правило не имеет требуемого вида). Пример 1.5.9. Грамматика
праволинейная. Она порождает язык Пример 1.5.10. Грамматика
праволинейная. Пример 1.5.11. Грамматика
праволинейная. Обобщенный вариант языка, порождаемого этой грамматикой, используется в доказательстве разрешимости арифметики Пресбургера. Определение 1.5.12. Правила вида Лемма 1.5.13. Каждая праволинейная грамматика является линейной. Каждая линейная грамматика является контекстно-свободной. Каждая контекстно-свободная грамматика без
Определение 1.5.14. Классы грамматик типа 0, 1, 2 и 3 образуют иерархию Хомского (Chomsky hierarchy). Определение 1.5.15. Язык называется языком типа 0 (контекстным языком, контекстно-свободным языком, линейным языком, праволинейным языком), если он порождается некоторой грамматикой типа 0 (соответственно контекстной грамматикой, контекстно-свободной грамматикой, линейной грамматикой, праволинейной грамматикой). Контекстно-свободные языки называются также алгебраическими языками. Пример 1.5.16. Пусть дан произвольный алфавит
Тогда язык
Два наиболее распространенных способа конечного задания формального языка - это грамматики и автоматы. Автоматами в данном контексте называют математические модели некоторых вычислительных устройств. В этой лекции рассматриваются конечные автоматы, соответствующие в иерархии Хомского праволинейным грамматикам. Более сильные вычислительные модели будут определены позже, в лекциях "10", "14" и "15". Термин "автоматный язык" закреплен за языками, распознаваемыми именно конечными автоматами, а не какими-либо более широкими семействами автоматов (например, автоматами с магазинной памятью или линейно ограниченными автоматами). В разделе 2.1 определяются понятия конечного автомата (для ясности такой автомат можно называть недетерминированным конечным автоматом) и распознаваемого конечным автоматом языка. В следующем разделе дается другое, но эквивалентное первому определение языка, распознаваемого конечным автоматом. Оно не является необходимым для дальнейшего изложения, но именно это определение поддается обобщению на случаи автоматов других типов. В разделе 2.3 доказывается, что тот же класс автоматных языков можно получить, используя лишь конечные автоматы специального вида (они читают на каждом такте ровно один символ и имеют ровно одно начальное состояние). Во многих учебниках конечными автоматами называют именно такие автоматы. Целую серию классических результатов теории формальных языков составляют теоремы о точном соответствии некоторых классов грамматик некоторым классам автоматов. Первая теорема из этой серии, утверждающая, что праволинейные грамматики порождают в точности автоматные языки, доказывается в разделе 2.4. Другая серия результатов связана с возможностью сузить некоторый класс грамматик, не изменив при этом класс порождаемых ими языков. Обычно в таком случае грамматики из меньшего класса называются грамматиками в нормальной форме. В разделе 2.5* формулируется результат такого типа для праволинейных грамматик. Сама эта теорема не представляет большого интереса, но аналогичные результаты, доказываемые позже для контекстно-свободных грамматик, используются во многих доказательствах и алгоритмах. Не все конечные автоматы подходят для конструирования распознающих устройств, пригодных для практических приложений, так как в общем случае конечный автомат не дает точного указания, как поступать на очередном шаге, а разрешает продолжать вычислительный процесс несколькими способами. Этого недостатка нет у детерминированных конечных автоматов (частного случая недетерминированных конечных автоматов), определенных в разделе 2.6. В разделе 2.7 доказывается, что каждый автоматный язык задается некоторым детерминированным конечным автоматом.
Примеры неавтоматных языков Пример 3.4.1. Рассмотрим язык Замечание 3.4.3. Условие, сформулированное в лемме 3.3.1, является необходимым для автоматности, но не достаточным. Пример 3.4.4. Пусть
Лемма 3.4.5*. Пусть L - автоматный язык над алфавитом Доказательство. Пусть L распознается конечным автоматом Эта лекция содержит дополнительные результаты, не используемые в дальнейшем изложении. В начале лекции доказывается замкнутость класса всех автоматных языков относительно взятия гомоморфного образа и относительно взятия полного гомоморфного прообраза. В разделе 4.2* определяются понятия побуквенного гомоморфизма и локального языка и доказывается еще один критерий автоматности: среди языков, не содержащих пустого слова, автоматными являются в точности образы локальных языков при побуквенных гомоморфизмах. В последнем разделе этой лекции устанавливается числовой критерий автоматности для языков над однобуквенным алфавитом (в терминах арифметических прогрессий) и доказывается связанное с длинами слов необходимое условие автоматности (для произвольного алфавита). Теорема Клини Определение 5.3.1. Назовем обобщенным конечным автоматом аналог конечного автомата, где переходы помечены не словами, а регулярными выражениями. Метка пути такого автомата - произведение регулярных выражений на переходах данного пути. Слово w допускается обобщенным конечным автоматом, если оно принадлежит языку, задаваемому меткой некоторого успешного пути. Замечание 5.3.2. Каждый конечный автомат можно преобразовать в обобщенный конечный автомат, допускающий те же слова. Для этого достаточно заменить всюду в метках переходов пустое слово на 1, а каждое непустое слово - на произведение его букв. Замечание 5.3.3. Если к обобщенному конечному автомату добавить переход с меткой 0, то множество допускаемых этим автоматом слов не изменится. Пример 5.3.4. Пусть
допускает все слова в алфавите Теорема 5.3.5 (теорема Клини). Язык L является регулярным тогда и только тогда, когда он является автоматным. Доказательство. Пусть e - регулярное выражение. Индукцией по построению e легко показать, что задаваемый им язык является автоматным (см. теорему 3.1.1). Обратно, пусть язык L распознается некоторым (недетерминированным) конечным автоматом с одним начальным состоянием и одним заключительным состоянием. Существует эквивалентный ему обобщенный конечный автомат Устраним по очереди все состояния, кроме q1 и q2. При устранении состояния q нужно для каждого перехода вида После устранения всех состояний, кроме q1 и q2, получится обобщенный конечный автомат
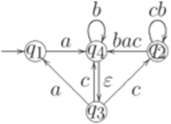
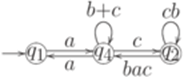
Очевидно, что Пример 5.3.6. Рассмотрим язык, распознаваемый конечным автоматом
где
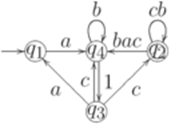
Тот же язык порождается обобщенным конечным автоматом
где
После устранения состояния q3 получается обобщенный конечный автомат
где
Можно упростить регулярные выражения и получить
После устранения состояния q4 и упрощения регулярных выражений получается обобщенный конечный автомат
где
Следовательно, язык L(M) задается регулярным выражением
Упростив это регулярное выражение, получим
5.4*. Звездная высота Определение 5.4.1. Звездная высота (star-height) регулярного выражения (обозначение sh(e)) определяется рекурсивно следующим образом:
Пример 5.4.2. Пусть Определение 5.4.3. Звездной высотой регулярного языка L (обозначение sh(L)) называется минимум звездных высот регулярных выражений, задающих этот язык. Замечание 5.4.4. Регулярный язык L является конечным тогда и только тогда, когда sh(L) = 0. Теорема 5.4.5. Пусть Доказательство можно найти в книге Саломаа А. Жемчужины теории формальных языков. - М.: Мир, 1986 с.41-46. Пример 5.4.6. Пусть
Тогда sh(L) = 2. Действительно, язык L задается регулярным выражением (ab+ba+(aa+bb)(ab+ba)*(aa+bb))* и не задается никаким регулярным выражением меньшей звездной высоты. Замечание 5.4.7. Неизвестно, верен ли аналог теоремы 5.4.5 для обобщенных регулярных выражений, в которых, помимо итерации, конкатенации и объединения, разрешена операция дополнения.
Основная цель данной лекции - доказать еще один критерий автоматности формального языка. Этот критерий можно сформулировать в терминах классов эквивалентности слов по взаимозаменяемости (однако формальные определения будут даны без использования понятия класса эквивалентности). Слова x и y считаются взаимозаменяемыми (относительно языка L), если при замене в любом слове из языка L подслова, совпадающего с x, на y снова получится слово из языка L и наоборот. В разделе 6.3 фактически доказывается, что язык L является автоматным тогда и только тогда, когда соответствующее отношение взаимозаменяемости разбивает множество всех слов рассматриваемого алфавита на конечное число классов эквивалентности. Но сначала мы докажем аналогичный результат для отношения взаимозаменяемости не подслов, а префиксов (раздел 6.1). Соответствующие классы эквивалентности слов позволяют построить минимальный детерминированный конечный автомат для заданного языка. Известен и другой метод нахождения минимального детерминированного конечного автомата (раздел 6.2), но этот метод можно применять только тогда, когда уже имеется какой-нибудь детерминированный конечный автомат, распознающий данный язык. В конце лекции доказывается, что классы эквивалентности по взаимозаменяемости относительно автоматного языка сами являются автоматными языками. Множества правых контекстов Определение 6.1.1. Пусть
Пример 6.1.2. Пусть 1. 2. если 3. если 4. если Определение 6.1.3. Для любого состояния p полного детерминированного конечного автомата Лемма 6.1.4. Если язык L распознается полным детерминированным конечным автоматом
Доказательство. Пусть I = {s}. Введем обозначение
Определим функцию Заметим, что для любых слов u и v, если Пример 6.1.5. Рассмотрим язык L, порождаемый полным детерминированным конечным автоматом
Лемма 6.1.6. Если Доказательство. Язык L распознается полным детерминированным конечным автоматом
Пример 6.1.7. Пусть
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 82; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.46.36 (0.217 с.) |
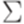 называется конечная последовательность элементов
называется конечная последовательность элементов 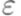 .
.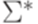 .
.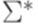 счетно. В самом деле, в алфавите
счетно. В самом деле, в алфавите  .
.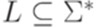 , то L называется языком (или формальным языком) над алфавитом
, то L называется языком (или формальным языком) над алфавитом  ).
). называется дополнением языка L относительно алфавита
называется дополнением языка L относительно алфавита 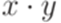 .
.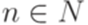 , то через xn обозначается слово
, то через xn обозначается слово  . Положим
. Положим  (знак
(знак  читается "равно по определению"). Всюду далее показатели над словами и символами, как правило, являются натуральными числами.
читается "равно по определению"). Всюду далее показатели над словами и символами, как правило, являются натуральными числами.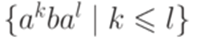 является языком над алфавитом {a,b}. Этот язык содержит слова b, ba, aba, baa, abaa, baaa, aabaa, abaaa, baaaa и т. д.
является языком над алфавитом {a,b}. Этот язык содержит слова b, ba, aba, baa, abaa, baaa, aabaa, abaaa, baaaa и т. д. .
.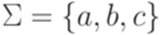 , то |baaa|a = 3, |baaa|b = 1 и |baaa|c = 0.
, то |baaa|a = 3, |baaa|b = 1 и |baaa|c = 0.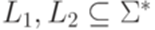 . Тогда
. Тогда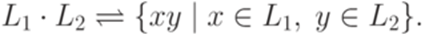
 называется конкатенацией языков L1 и L2.
называется конкатенацией языков L1 и L2.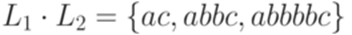 .
.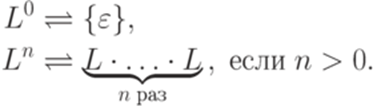
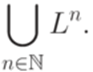
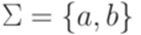 и L = {aa,ab,ba,bb}, то
и L = {aa,ab,ba,bb}, то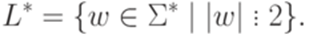
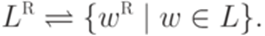
 ), если y = xu для некоторого слова u.
), если y = xu для некоторого слова u.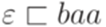 ,
, 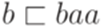 ,
, 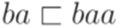 и
и 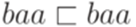 .
.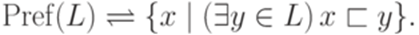
 ), если y = ux для некоторого слова u.
), если y = ux для некоторого слова u.
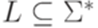 . Тогда через Subw(L) обозначается множество, состоящее из всех подслов слов языка L. Множество Subw(L) называется множеством подслов языка L.
. Тогда через Subw(L) обозначается множество, состоящее из всех подслов слов языка L. Множество Subw(L) называется множеством подслов языка L. ) называется подпоследовательностью (subsequence) слова y, если существуют такие слова u0, u1,..., un, что u0a1u1a2...anun = y.
) называется подпоследовательностью (subsequence) слова y, если существуют такие слова u0, u1,..., un, что u0a1u1a2...anun = y.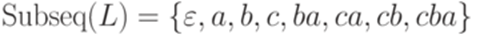 .
.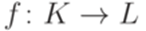 называется биекцией (bijection), если каждый элемент множества Lявляется образом ровно одного элемента множества K (относительно функции f).
называется биекцией (bijection), если каждый элемент множества Lявляется образом ровно одного элемента множества K (относительно функции f).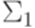 и
и 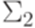 - алфавиты. Если отображение
- алфавиты. Если отображение 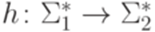 удовлетворяет условию
удовлетворяет условию 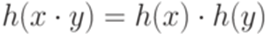 для всех слов
для всех слов  и
и  , то отображение h называется гомоморфизмом (морфизмом).
, то отображение h называется гомоморфизмом (морфизмом).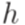 - гомоморфизм, то
- гомоморфизм, то 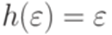 .
.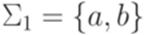 и
и  . Тогда отображение
. Тогда отображение  , является гомоморфизмом.
, является гомоморфизмом.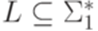 , то через h(L) обозначается язык
, то через h(L) обозначается язык 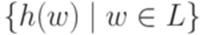 .
.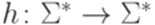 задан равенствами h(a) = abba и
задан равенствами h(a) = abba и 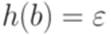 . Тогда
. Тогда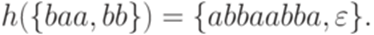
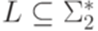 , то через h-1(L) обозначается язык
, то через h-1(L) обозначается язык 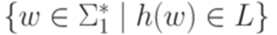 .
.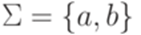 . Пусть гомоморфизм
. Пусть гомоморфизм 
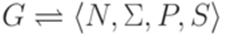 , где N и
, где N и 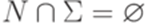 ,
, 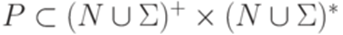 , P конечно и
, P конечно и 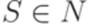 . Здесь
. Здесь  называются правилами подстановки, просто правилами или продукциями (rewriting rule, production) и записываются в виде
называются правилами подстановки, просто правилами или продукциями (rewriting rule, production) и записываются в виде  .
. . Тогда
. Тогда 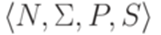 является порождающей грамматикой.
является порождающей грамматикой.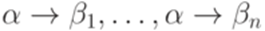 часто используют сокращенную запись
часто используют сокращенную запись  .
.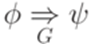 , если
, если 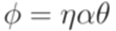 ,
, 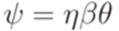 и
и 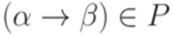 для некоторых слов
для некоторых слов 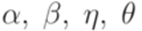 в алфавите
в алфавите  . Если
. Если 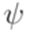 непосредственно выводимо из слова
непосредственно выводимо из слова 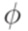 .
.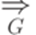 можно писать просто
можно писать просто 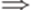 .
.
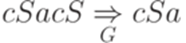 .
.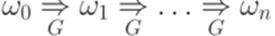 , где
, где 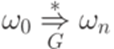 и говорим, что слово
и говорим, что слово 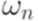 выводимо из слова
выводимо из слова 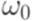 . Другими словами, бинарное отношение
. Другими словами, бинарное отношение 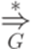 является рефлексивным, транзитивным замыканием бинарного отношения
является рефлексивным, транзитивным замыканием бинарного отношения  .
.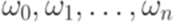 называется выводом (derivation) слова
называется выводом (derivation) слова 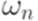 из слова
из слова 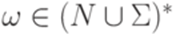 имеет место
имеет место  (так как возможен вывод длины 0).
(так как возможен вывод длины 0). . Тогда
. Тогда  . Длина этого вывода - 3.
. Длина этого вывода - 3.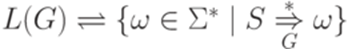 . Будем также говорить, что грамматика G порождает (generates) язык L(G).
. Будем также говорить, что грамматика G порождает (generates) язык L(G).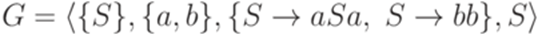 , то
, то 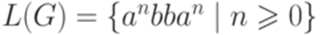 .
.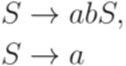
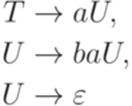
 , где
, где 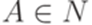 ,
, 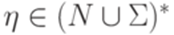 ,
, 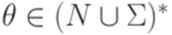 ,
, 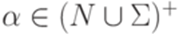 .
.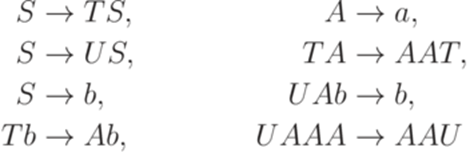
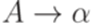 , где
, где 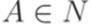 ,
, 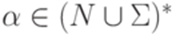 .
.
 или
или 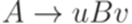 , где
, где 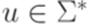 ,
, 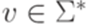 ,
, 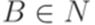 .
.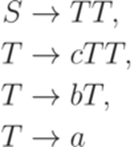
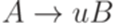 , где
, где 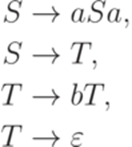
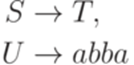
 .
.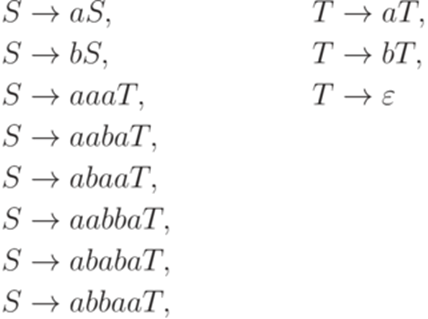

 называются
называются 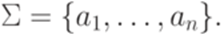
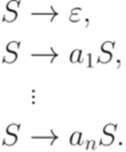
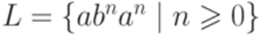 над алфавитом
над алфавитом 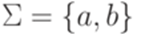 . Утверждение леммы 3.3.1 не выполняется ни для какого натурального числа p. Действительно, если w = abpap, то x = abk, y = bm, z = bp-k-map для некоторых
. Утверждение леммы 3.3.1 не выполняется ни для какого натурального числа p. Действительно, если w = abpap, то x = abk, y = bm, z = bp-k-map для некоторых 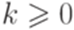 и
и 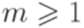 или
или  , y = abl, z = bp-lap для некоторого
, y = abl, z = bp-lap для некоторого 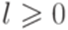 . В обоих случаях
. В обоих случаях 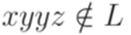 . Таким образом, язык L не является автоматным.
. Таким образом, язык L не является автоматным.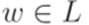 длины не меньше p найдутся слова
длины не меньше p найдутся слова 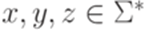 , соответствующие утверждению леммы 3.3.1. Тем не менее язык L не является автоматным, так как
, соответствующие утверждению леммы 3.3.1. Тем не менее язык L не является автоматным, так как
 и
и 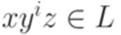 для всех
для всех 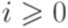 . Здесь [m] означает целую часть числа m.
. Здесь [m] означает целую часть числа m. , содержащим только переходы с метками длины единица. Положим p = |Q|. Пусть слово w является меткой успешного пути
, содержащим только переходы с метками длины единица. Положим p = |Q|. Пусть слово w является меткой успешного пути  . Обозначим l = [|w|/p]. Если l = 0, то положим
. Обозначим l = [|w|/p]. Если l = 0, то положим  . Пусть
. Пусть 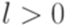 . Согласно принципу Дирихле найдутся такие натуральные числа j и k, что
. Согласно принципу Дирихле найдутся такие натуральные числа j и k, что 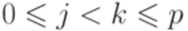 и qjl = qkl. Выберем слова x, y и z так, что |x| = jl, |y| = kl - jl и xyz = w.
и qjl = qkl. Выберем слова x, y и z так, что |x| = jl, |y| = kl - jl и xyz = w.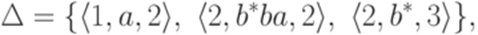
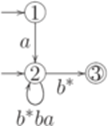
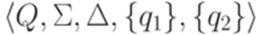 , где
, где 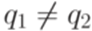 . Если есть несколько переходов с общим началом и общим концом (такие переходы называются параллельными), заменим их на один переход, используя операцию +.
. Если есть несколько переходов с общим началом и общим концом (такие переходы называются параллельными), заменим их на один переход, используя операцию +.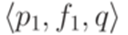 , где
, где  , и для каждого перехода вида
, и для каждого перехода вида 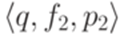 , где
, где 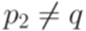 , добавить переход
, добавить переход 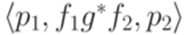 , где регулярное выражение g - метка перехода из q в q (если нет перехода из q в q, то надо добавить переход
, где регулярное выражение g - метка перехода из q в q (если нет перехода из q в q, то надо добавить переход 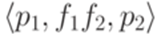 ), и снова всюду заменить параллельные переходы на один переход, используя операцию +.
), и снова всюду заменить параллельные переходы на один переход, используя операцию +.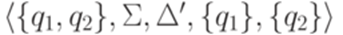 , где
, где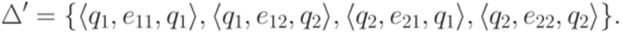
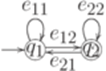
 .
.
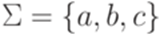 и
и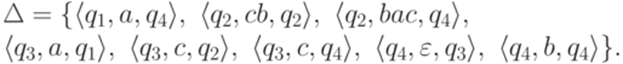
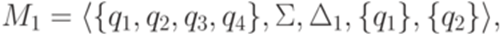
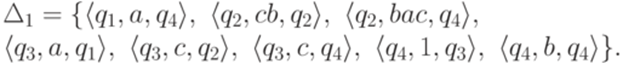
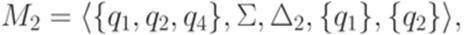
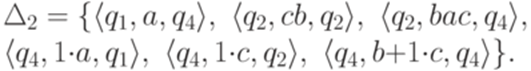
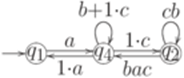
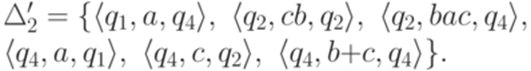
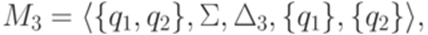
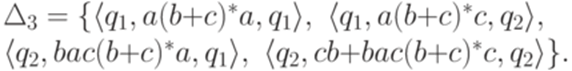
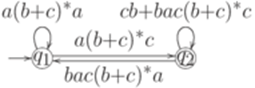
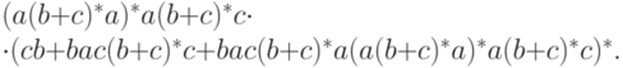
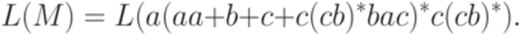
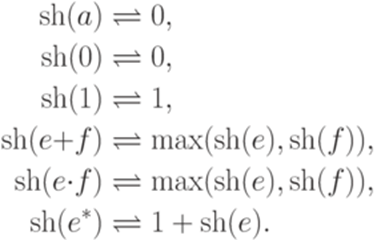
 . Тогда для любого
. Тогда для любого 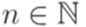 существует такой регулярный язык
существует такой регулярный язык 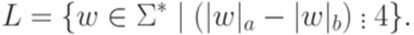
 . Тогда множество правых контекстов слова y относительно языка Lопределяется следующим образом:
. Тогда множество правых контекстов слова y относительно языка Lопределяется следующим образом:
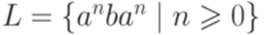 . Тогда
. Тогда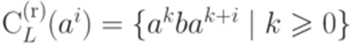
 , то
, то 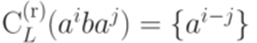 ;
;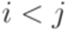 , то
, то 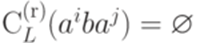 ;
;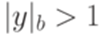 , то
, то 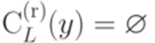 .
. и любого слова w обозначим через
и любого слова w обозначим через  такое состояние q, что существует путь из p в q с меткой w (в силу полноты и детерминированности такое состояние существует и единственно).
такое состояние q, что существует путь из p в q с меткой w (в силу полноты и детерминированности такое состояние существует и единственно).

 , положив f(A) равным
, положив f(A) равным 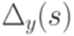 , где y - некоторое слово, для которого выполнено условие
, где y - некоторое слово, для которого выполнено условие 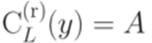 (если существует несколько таких слов y, то можно использовать, например, первое среди них в лексикографическом порядке).
(если существует несколько таких слов y, то можно использовать, например, первое среди них в лексикографическом порядке).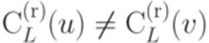 , то
, то  . Следовательно, функция f является инъективной. Но тогда
. Следовательно, функция f является инъективной. Но тогда 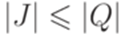 .
.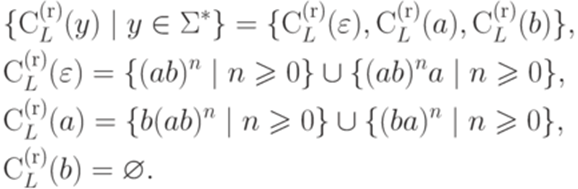
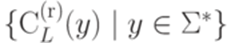 конечно, то язык L является автоматным.
конечно, то язык L является автоматным.