
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение регулярного выражения
Определение 5.1.1. Регулярное выражение над алфавитом Для экономии скобок будем считать, что операция * связывает сильнее (то есть имеет более высокий приоритет), чем умножение, а умножение связывает сильнее, чем сложение. Вместо Пример 5.1.2. Пусть Определение 5.1.3. Каждое регулярное выражение e над алфавитом
Заметим, что в правой части последнего выражения символом * обозначена итерация языка (см. определение 1.2.7). Вместо Пример 5.1.4. Пусть
Определение 5.1.5. Язык L называется регулярным если он задается некоторым регулярным выражением. Определение 5.1.6. Пусть e - регулярное выражение. Тогда 5.2*. Свойства регулярных выражений Лемма 5.2.1. Регулярные выражения образуют ассоциативное полукольцо с операциями 1. e+f = f+e; 2. e+0 = e; 3. 4. 5. 6. 7. 8. 9. 10. Равенство понимается как равенство языков, задаваемых регулярными выражениями. Лемма 5.2.2. Для любых регулярных выражений e и f выполняются следующие тождества: 1. e+e = e; 2. (1+e+ee+...+en-1)(en)* = e* для любого 3. (e*f)*e* = (e+f)*; 4. 1+e(fe)*f = (ef)*. Лемма 5.2.3. Для любых регулярных выражений e, f и g, если e = ef+g и Теорема Клини Определение 5.3.1. Назовем обобщенным конечным автоматом аналог конечного автомата, где переходы помечены не словами, а регулярными выражениями. Метка пути такого автомата - произведение регулярных выражений на переходах данного пути. Слово w допускается обобщенным конечным автоматом, если оно принадлежит языку, задаваемому меткой некоторого успешного пути. Замечание 5.3.2. Каждый конечный автомат можно преобразовать в обобщенный конечный автомат, допускающий те же слова. Для этого достаточно заменить всюду в метках переходов пустое слово на 1, а каждое непустое слово - на произведение его букв.
Замечание 5.3.3. Если к обобщенному конечному автомату добавить переход с меткой 0, то множество допускаемых этим автоматом слов не изменится. Пример 5.3.4. Пусть
допускает все слова в алфавите Теорема 5.3.5 (теорема Клини). Язык L является регулярным тогда и только тогда, когда он является автоматным. Доказательство. Пусть e - регулярное выражение. Индукцией по построению e легко показать, что задаваемый им язык является автоматным (см. теорему 3.1.1). Обратно, пусть язык L распознается некоторым (недетерминированным) конечным автоматом с одним начальным состоянием и одним заключительным состоянием. Существует эквивалентный ему обобщенный конечный автомат Устраним по очереди все состояния, кроме q1 и q2. При устранении состояния q нужно для каждого перехода вида После устранения всех состояний, кроме q1 и q2, получится обобщенный конечный автомат
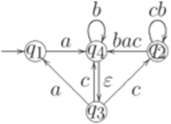
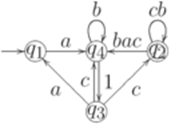
Очевидно, что Пример 5.3.6. Рассмотрим язык, распознаваемый конечным автоматом
где
Тот же язык порождается обобщенным конечным автоматом
где
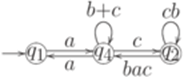
После устранения состояния q3 получается обобщенный конечный автомат
где
Можно упростить регулярные выражения и получить
После устранения состояния q4 и упрощения регулярных выражений получается обобщенный конечный автомат
где
Следовательно, язык L(M) задается регулярным выражением
Упростив это регулярное выражение, получим
5.4*. Звездная высота Определение 5.4.1. Звездная высота (star-height) регулярного выражения (обозначение sh(e)) определяется рекурсивно следующим образом:
Пример 5.4.2. Пусть
Определение 5.4.3. Звездной высотой регулярного языка L (обозначение sh(L)) называется минимум звездных высот регулярных выражений, задающих этот язык. Замечание 5.4.4. Регулярный язык L является конечным тогда и только тогда, когда sh(L) = 0. Теорема 5.4.5. Пусть Доказательство можно найти в книге Саломаа А. Жемчужины теории формальных языков. - М.: Мир, 1986 с.41-46. Пример 5.4.6. Пусть
Тогда sh(L) = 2. Действительно, язык L задается регулярным выражением (ab+ba+(aa+bb)(ab+ba)*(aa+bb))* и не задается никаким регулярным выражением меньшей звездной высоты. Замечание 5.4.7. Неизвестно, верен ли аналог теоремы 5.4.5 для обобщенных регулярных выражений, в которых, помимо итерации, конкатенации и объединения, разрешена операция дополнения.
Основная цель данной лекции - доказать еще один критерий автоматности формального языка. Этот критерий можно сформулировать в терминах классов эквивалентности слов по взаимозаменяемости (однако формальные определения будут даны без использования понятия класса эквивалентности). Слова x и y считаются взаимозаменяемыми (относительно языка L), если при замене в любом слове из языка L подслова, совпадающего с x, на y снова получится слово из языка L и наоборот. В разделе 6.3 фактически доказывается, что язык L является автоматным тогда и только тогда, когда соответствующее отношение взаимозаменяемости разбивает множество всех слов рассматриваемого алфавита на конечное число классов эквивалентности. Но сначала мы докажем аналогичный результат для отношения взаимозаменяемости не подслов, а префиксов (раздел 6.1). Соответствующие классы эквивалентности слов позволяют построить минимальный детерминированный конечный автомат для заданного языка. Известен и другой метод нахождения минимального детерминированного конечного автомата (раздел 6.2), но этот метод можно применять только тогда, когда уже имеется какой-нибудь детерминированный конечный автомат, распознающий данный язык. В конце лекции доказывается, что классы эквивалентности по взаимозаменяемости относительно автоматного языка сами являются автоматными языками. Множества правых контекстов Определение 6.1.1. Пусть
Пример 6.1.2. Пусть 1. 2. если 3. если 4. если Определение 6.1.3. Для любого состояния p полного детерминированного конечного автомата Лемма 6.1.4. Если язык L распознается полным детерминированным конечным автоматом
Доказательство. Пусть I = {s}. Введем обозначение
Определим функцию Заметим, что для любых слов u и v, если Пример 6.1.5. Рассмотрим язык L, порождаемый полным детерминированным конечным автоматом
Лемма 6.1.6. Если Доказательство. Язык L распознается полным детерминированным конечным автоматом
Пример 6.1.7. Пусть
Тогда
Теорема 6.1.8. Язык Доказательство. Необходимость доказана в лемме 6.1.4, достаточность - в лемме 6.1.6. Замечание 6.1.9. В силу леммы 6.1.4 полный детерминированный конечный автомат, построенный в доказательстве леммы 6.1.6, является минимальным (по количеству состояний) среди всех полных детерминированных конечных автоматов, распознающих заданный язык. Можно доказать, что любой минимальный полный детерминированный конечный автомат, распознающий заданный язык, изоморфен этому автомату.
|
|||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 65; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.197.132 (0.027 с.) |
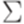 определяется рекурсивно следующим образом: 0 является регулярным выражением; 1 является регулярным выражением; если
определяется рекурсивно следующим образом: 0 является регулярным выражением; 1 является регулярным выражением; если 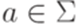 , то a является регулярным выражением; если e и f являются регулярными выражениями, то
, то a является регулярным выражением; если e и f являются регулярными выражениями, то 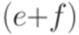 ,
, 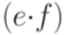 и
и 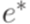 тоже являются регулярными выражениями.
тоже являются регулярными выражениями.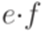 часто пишут просто
часто пишут просто 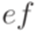 .
.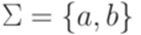 . Тогда
. Тогда 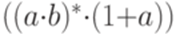 является регулярным выражением над алфавитом
является регулярным выражением над алфавитом  ), определяемое рекурсивно следующим образом:
), определяемое рекурсивно следующим образом: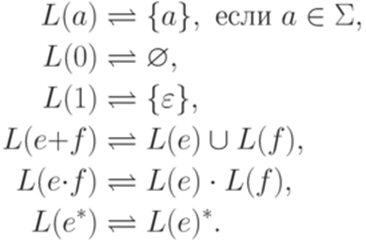
 часто пишут просто e.
часто пишут просто e.
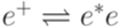 .
.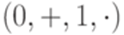 , то есть для любых регулярных выражений e, f и g выполняются следующие тождества:
, то есть для любых регулярных выражений e, f и g выполняются следующие тождества: ;
; ;
; ;
; ;
; ;
; ;
; ;
;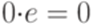 .
. ;
;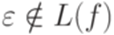 , то e = gf*.
, то e = gf*.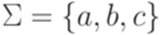 . Обобщенный конечный автомат
. Обобщенный конечный автомат  , где Q = {1,2,3}, I = {1,2}, F = {3},
, где Q = {1,2,3}, I = {1,2}, F = {3},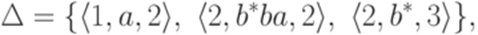
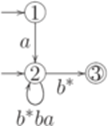
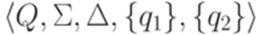 , где
, где 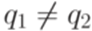 . Если есть несколько переходов с общим началом и общим концом (такие переходы называются параллельными), заменим их на один переход, используя операцию +.
. Если есть несколько переходов с общим началом и общим концом (такие переходы называются параллельными), заменим их на один переход, используя операцию +.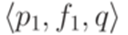 , где
, где  , и для каждого перехода вида
, и для каждого перехода вида 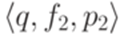 , где
, где 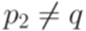 , добавить переход
, добавить переход 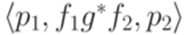 , где регулярное выражение g - метка перехода из q в q (если нет перехода из q в q, то надо добавить переход
, где регулярное выражение g - метка перехода из q в q (если нет перехода из q в q, то надо добавить переход 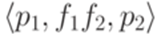 ), и снова всюду заменить параллельные переходы на один переход, используя операцию +.
), и снова всюду заменить параллельные переходы на один переход, используя операцию +.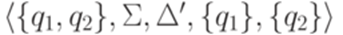 , где
, где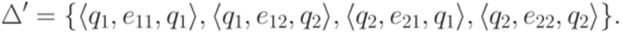
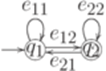
 .
.
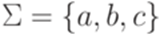 и
и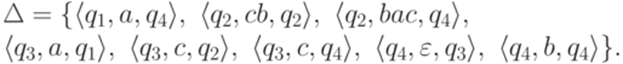
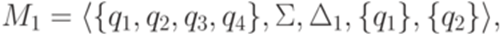
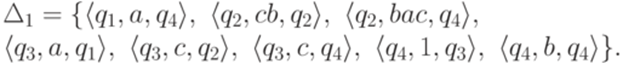
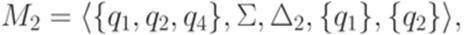
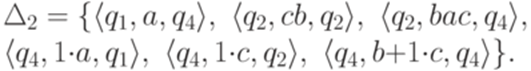
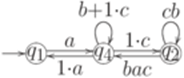
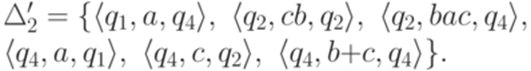
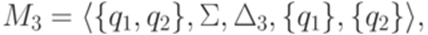
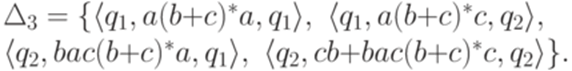
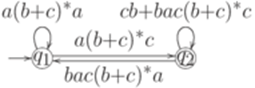
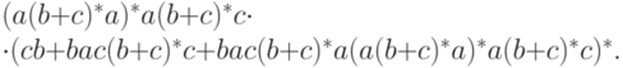
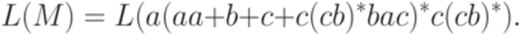
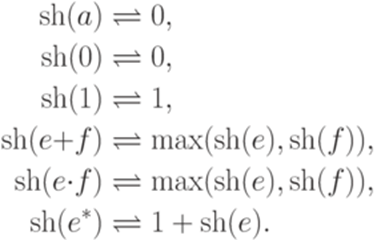
 . Тогда для любого
. Тогда для любого 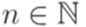 существует такой регулярный язык
существует такой регулярный язык 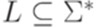 , что sh(L) = n.
, что sh(L) = n.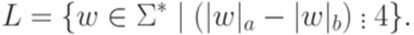
 . Тогда множество правых контекстов слова y относительно языка Lопределяется следующим образом:
. Тогда множество правых контекстов слова y относительно языка Lопределяется следующим образом:
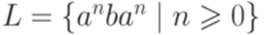 . Тогда
. Тогда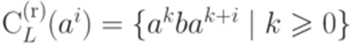
 , то
, то 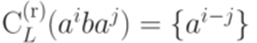 ;
;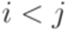 , то
, то 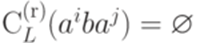 ;
;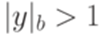 , то
, то 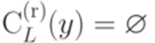 .
. и любого слова w обозначим через
и любого слова w обозначим через  такое состояние q, что существует путь из p в q с меткой w (в силу полноты и детерминированности такое состояние существует и единственно).
такое состояние q, что существует путь из p в q с меткой w (в силу полноты и детерминированности такое состояние существует и единственно).

 , положив f(A) равным
, положив f(A) равным 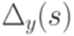 , где y - некоторое слово, для которого выполнено условие
, где y - некоторое слово, для которого выполнено условие 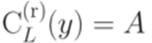 (если существует несколько таких слов y, то можно использовать, например, первое среди них в лексикографическом порядке).
(если существует несколько таких слов y, то можно использовать, например, первое среди них в лексикографическом порядке).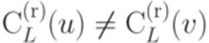 , то
, то  . Следовательно, функция f является инъективной. Но тогда
. Следовательно, функция f является инъективной. Но тогда 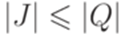 .
.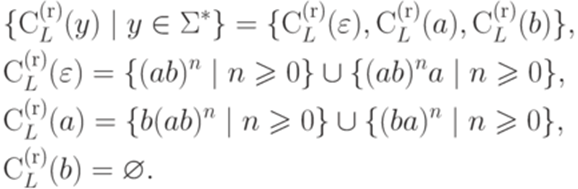
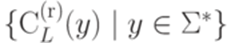 конечно, то язык L является автоматным.
конечно, то язык L является автоматным.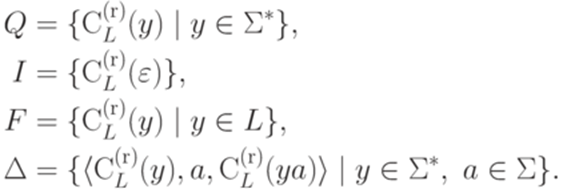
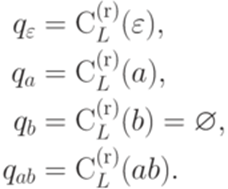
 . Язык L распознается полным детерминированным конечным автоматом
. Язык L распознается полным детерминированным конечным автоматом 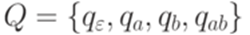 ,
, 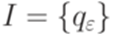 ,
, 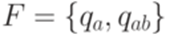 ,
,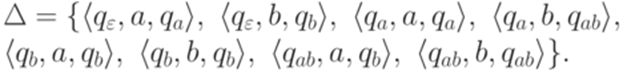
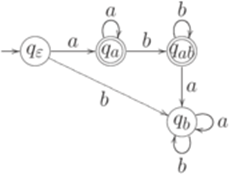
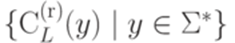 конечно.
конечно.


