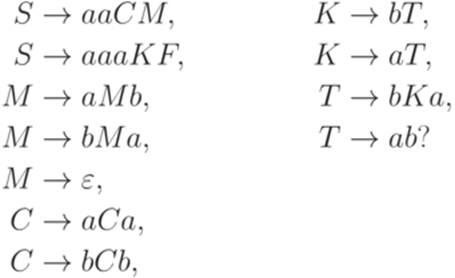Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разрешимые и перечислимые множестваСодержание книги
Поиск на нашем сайте Определение 14.2.1. Говорят, что детерминированная машина Тьюринга
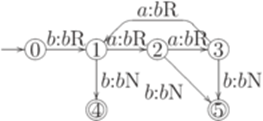
с выделенным состоянием qa разрешает (decides) язык 1) для каждого слова 2) для каждого слова Пример 14.2.2. Рассмотрим детерминированную машину Тьюринга
где
Эта машина Тьюринга разрешает язык Определение 14.2.3. Язык L над алфавитом
(с выделенным состоянием qa), которая разрешает язык L. Определение 14.2.4. Говорят, что машина Тьюринга
допускает (принимает, accepts) слово Определение 14.2.5. Язык, допускаемый машиной Тьюринга M, - это язык, состоящий из всех допускаемых данной машиной Тьюринга слов. Определение 14.2.6. Язык называется перечислимым (рекурсивно перечислимым, полуразрешимым, recursively enumerable), если существует детерминированная машина Тьюринга, допускающая этот язык. Замечание 14.2.7. В определении 14.2.6 можно отбросить требование детерминированности машины Тьюринга. Теорема 14.2.8. Каждый разрешимый язык является перечислимым. Доказательство. Пусть дана машина Тьюринга
с выделенным состоянием qa, которая разрешает язык
допускает язык L. Пример 14.2.9. Если в машине Тьюринга из примера 14.1.15 заменить переход Теорема 14.2.10. Существует такая машина Тьюринга над однобуквенным алфавитом Доказательство. Доказательство существования перечислимого неразрешимого множества можно найти, например, в [31, 9.2]. Упражнение 14.2.11. Найти детерминированную машину Тьюринга с входным алфавитом {a}, разрешающую язык Упражнение 14.2.12. Найти детерминированную машину Тьюринга с входным алфавитом {a}, допускающую язык Массовые задачи Определение 14.3.1. Массовой задачей (problem) называется бесконечная серия "однотипных" индивидуальных задач (instance), каждая из которых имеет определенный ответ. С каждой массовой задачей связана некоторая фиксированная схема кодирования (encoding scheme), которая отображает индивидуальные задачи в их коды - слова в некотором фиксированном алфавите. При этом требуется, чтобы множество кодов всех индивидуальных задач было разрешимым. Определение 14.3.2. Задачей распознавания (decision problem) называется массовая задача, в которой ответами индивидуальных задач могут быть только "да" и "нет" (то есть существует только два возможных ответа). Пример 14.3.3. Зафиксируем некоторый алфавит Пусть # - новый символ, не принадлежащий алфавиту Эта массовая задача является задачей распознавания. Определение 14.3.4. Алгоритмическая проблема - проблема, в которой требуется найти алгоритм для решения массовой задачи. Если такой алгоритм существует, то данная проблема называется алгоритмически разрешимой или просто разрешимой (decidable, solvable), в противном случае ее называют алгоритмически неразрешимой (undecidable, unsolvable). Замечание 14.3.5. Алгоритмическая проблема, относящаяся к некоторой задаче распознавания, алгоритмически разрешима тогда и только тогда, когда разрешимо множество кодов индивидуальных задач с ответом "да". Пример 14.3.6. Рассмотрим массовую задачу из примера 14.3.3. Соответствующая алгоритмическая проблема разрешима, так как разрешим язык Пример 14.3.7. Зафиксируем некоторый алфавит
необходимо выяснить, является ли эта грамматика праволинейной. Для полной строгости необходимо договориться, как кодировать грамматику G в виде слова. Например, можно использовать алфавит
(над алфавитом
Легко понять, что соответствующая алгоритмическая проблема (проблема проверки праволинейности) разрешима. Упражнение 14.3.8. Разрешима ли алгоритмическая проблема распознавания четности длины слова над алфавитом {a,b}? 14.4*. Грамматики типа 0 Теорема 14.4.1. Класс языков, порождаемых грамматиками типа 0, совпадает с классом перечислимых языков. Доказательство можно найти, например, в [СерГал с. 24-26]. Упражнение 14.4.2. Выводимо ли слово aab в грамматике
Упражнение 14.4.3. Выводимо ли слово aaaaaaaab в грамматике
Замечание 14.4.4. Неизвестно, порождает ли грамматика
все слова в алфавите {a,b}. Упражнение 14.4.5. Пусть
Выводимо ли в ней слово ccdcdcddccddcdcccabba? Упражнение 14.4.6. Является ли разрешимым язык, порождаемый грамматикой
Определение 14.4.7. Порождающая грамматика в нормальной форме - это порождающая грамматика, в которой каждое правило имеет вид Теорема 14.4.8. Каждая порождающая грамматика эквивалентна некоторой порождающей грамматике в нормальной форме. Упражнение 14.4.9. Существует ли такая порождающая грамматика G, что язык Проблема соответствий Поста Определение 14.5.1. Постовской системой соответствия над алфавитом Замечание 14.5.2. Систему
Определение 14.5.3. Решением (match) постовской системы соответствия ((x1,...,xn),(y1,...,yn)) называется непустая последовательность индексов
где Пример 14.5.4. Пусть
Последовательность (2,1,3,2,2) является решением этой системы, так как
Упражнение 14.5.5. Пусть
Определение 14.5.6. Проблемой соответствий Поста (Post correspondence problem) называется проблема нахождения алгоритма, выясняющего для каждой постовской системы соответствия, существует ли решение этой системы. Теорема 14.5.7. Пусть Доказательство можно найти в [ХопМот, 9.4]. Упражнение 14.5.8. Существует ли решение у постовской системы соответствия Упражнение 14.5.9. Существует ли решение у постовской системы соответствия Упражнение 14.5.10. Существует ли решение у постовской системы соответствия Упражнение 14.5.11. Существует ли решение у постовской системы соответствия Упражнение 14.5.12. Существует ли решение у постовской системы соответствия Упражнение 14.5.13. Существует ли решение у постовской системы соответствия Упражнение 14.5.14. Существует ли решение у постовской системы соответствия Упражнение 14.5.15. Существует ли постовская система соответствия, имеющая ровно одно решение? В этой лекции рассматриваются наиболее известные разрешимые проблемы, связанные с грамматиками, автоматами и регулярными выражениями. Поскольку все приведенные выше доказательства эквивалентности разных способов конечного задания формального языка были конструктивными, не важно, какой из эквивалентных способов задания языка (например, посредством контекстно-свободной грамматики или автомата с магазинной памятью) используется в точной формулировке массовой задачи. Первые два раздела этой лекции посвящены контекстным языкам. В разделах 15.3-15.6 сформулированы теоремы о разрешимости для некоторых алгоритмических проблем. Доказательства этих теорем опираются на конструктивность рассуждений, проведенных в лекциях "3" и "8". В разделе 15.7* приводится новый неожиданный результат, доказанный в 1997 году. Проблема эквивалентности конечных автоматов (или, что то же самое, регулярных выражений) разрешима, но, к сожалению, она сложна, то есть нахождение ответа индивидуальной задачи требует (в некотором смысле) много времени. В разделе 15.9* указывается, что даже для регулярных выражений без итерации (которые, очевидно, соответствуют конечным автоматам без циклов) проблема неэквивалентности NP -полна (необходимые определения из теории сложности вычислений приведены в разделе 15.8*). Неукорачивающие грамматики Определение 15.1.1. Порождающая грамматика Теорема 15.1.2. Существует алгоритм, позволяющий по произвольной неукорачивающей грамматике G и по слову wузнать, верно ли, что Теорема 15.1.3. Каждая контекстная грамматика является неукорачивающей. Каждая неукорачивающая грамматика эквивалентна некоторой контекстной грамматике. Пример 15.1.4. Грамматика
эквивалентна контекстной грамматике из примера 1.5.4. Упражнение 15.1.5. Найти неукорачивающую грамматику, порождающую язык Упражнение 15.1.6. Найти неукорачивающую грамматику, порождающую язык Упражнение 15.1.7. Найти неукорачивающую грамматику, порождающую язык Упражнение 15.1.7. Найти неукорачивающую грамматику, порождающую язык 15.2*. Линейно ограниченные автоматы Определение 15.2.1. Машина Тьюринга
называется линейно ограниченным автоматом (linear bounded automaton), если не существует таких Теорема 15.2.2. Язык L, не содержащий пустого слова, порождается некоторой неукорачивающей грамматикой тогда и только тогда, когда существует линейно ограниченный автомат (в общем случае недетерминированный), допускающий язык L. Замечание 15.2.3. Неизвестно, верен ли аналог теоремы 15.2.2 для детерминированных линейно ограниченных автоматов. Теорема 15.2.4. Класс языков, порождаемых неукорачивающими грамматиками, то есть класс контекстных языков, замкнут относительно операций объединения, пересечения и дополнения. Замкнутость относительно операции дополнения доказали в 1987 году (независимо друг от друга) Нил Иммерман (Neil Immerman) и Роберт Селепчени (Robert Szelepcs) (см. [Imm, Sze]). Замкнутость относительно операции объединения очевидна, а пересечение выражается через объединение и дополнение. Упражнение 15.2.5. Является ли контекстным язык
Упражнение 15.2.6. Является ли контекстным язык
Проблема выводимости слова Теорема 15.3.1. Существует алгоритм, позволяющий по произвольной контекстно-свободной грамматике G узнать, верно ли, что Теорема 15.3.2. Существует алгоритм, позволяющий по произвольной контекстно-свободной грамматике G и по слову w узнать, верно ли, что Упражнение 15.3.3. Принадлежит ли слово aaaaabbbabb языку, порождаемому грамматикой
Упражнение 15.3.4. Принадлежит ли слово abababa языку, порождаемому грамматикой
Проблема пустоты языка Теорема 15.4.1. Существует алгоритм, позволяющий по произвольной контекстно-свободной грамматике G узнать, верно ли, что Доказательство. Удалим из G все бесполезные символы, кроме начального символа (как в доказательстве теоремы 8.1.3). Если полученная грамматика содержит хотя бы одно правило, то Упражнение 15.4.2. Является ли непустым язык, порождаемый грамматикой
|
||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 186; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.253.7 (0.007 с.) |

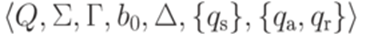
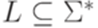 , если
, если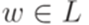 найдутся такие
найдутся такие 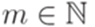 и
и 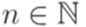 , что
, что 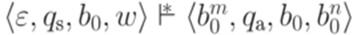 ;
;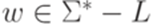 найдутся такие
найдутся такие 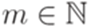 и
и 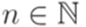 , что
, что  . Состояние qa называется допускающим (принимающим, accept state), состояние qr называется отвергающим (непринимающим, (reject state).
. Состояние qa называется допускающим (принимающим, accept state), состояние qr называется отвергающим (непринимающим, (reject state).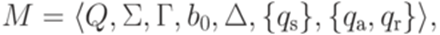
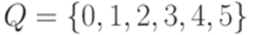 ,
, 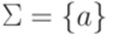 ,
, 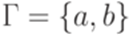 ,
,  ,
,  ,
,  ,
,  и
и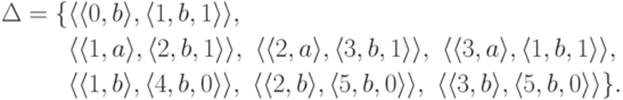
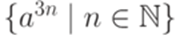 .
.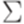 называется разрешимым или рекурсивным (decidable, recursive), если существует детерминированная машина Тьюринга
называется разрешимым или рекурсивным (decidable, recursive), если существует детерминированная машина Тьюринга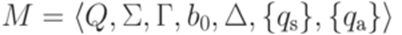
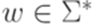 , если для некоторых
, если для некоторых 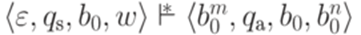 .
.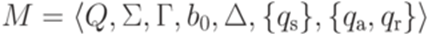
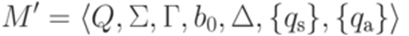
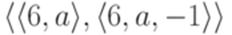 на
на 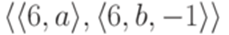 , то получится машина Тьюринга, допускающая язык
, то получится машина Тьюринга, допускающая язык 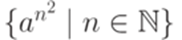 . Следовательно, этот язык является перечислимым. Можно доказать, что он даже является разрешимым.
. Следовательно, этот язык является перечислимым. Можно доказать, что он даже является разрешимым.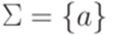 , что язык, допускаемый этой машиной Тьюринга, неразрешим.
, что язык, допускаемый этой машиной Тьюринга, неразрешим.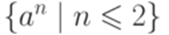 .
.
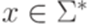 и
и  , необходимо выяснить, является ли слово x подсловом слова y.
, необходимо выяснить, является ли слово x подсловом слова y. .
.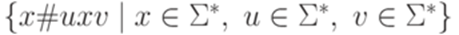 .
.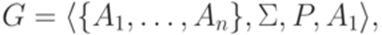
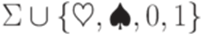 , где
, где  - дополнительные символы, не принадлежащие множеству
- дополнительные символы, не принадлежащие множеству  и кода числа i в двоичной системе счисления. В каждом правиле
и кода числа i в двоичной системе счисления. В каждом правиле  добавим символ
добавим символ  на месте
на месте  и после слова
и после слова 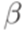 . Кодом грамматики G будем считать результат конкатенации кодов всех правил из множества P. Например, грамматика
. Кодом грамматики G будем считать результат конкатенации кодов всех правил из множества P. Например, грамматика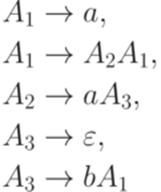
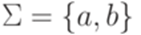 ) кодируется словом
) кодируется словом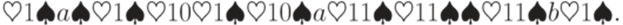
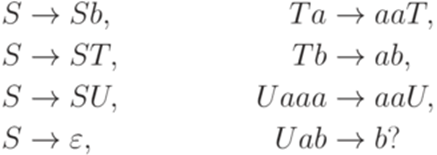
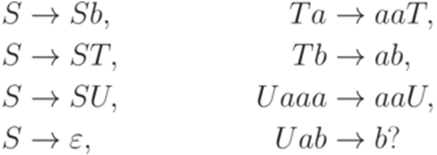
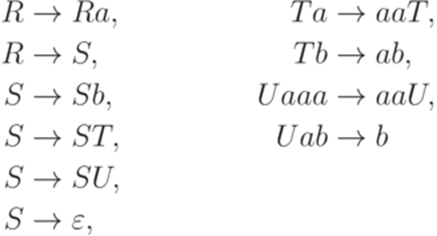
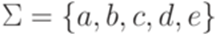 . Рассмотрим грамматику
. Рассмотрим грамматику
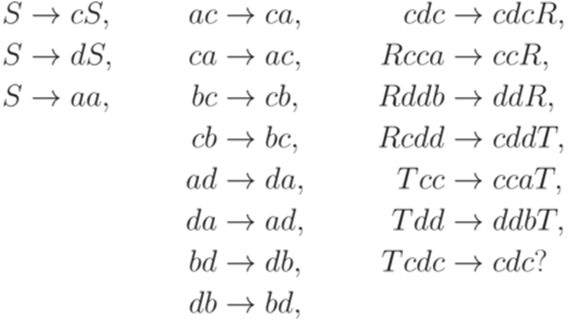
 ,
,  или
или 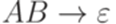 , где
, где 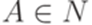 ,
, 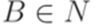 ,
, 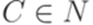 ,
, 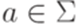 .
. не порождается ни одной грамматикой типа 0?
не порождается ни одной грамматикой типа 0?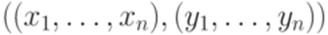 , где
, где 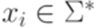 и
и 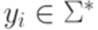 для всех i.
для всех i.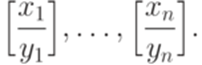
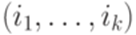 , удовлетворяющая условию
, удовлетворяющая условию
 для каждого j.
для каждого j.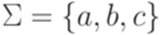 . Рассмотрим постовскую систему соответствия
. Рассмотрим постовскую систему соответствия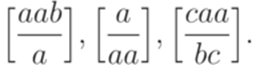
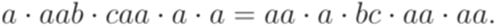
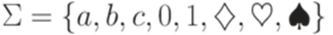 . Существует ли решение у постовской системы соответствия
. Существует ли решение у постовской системы соответствия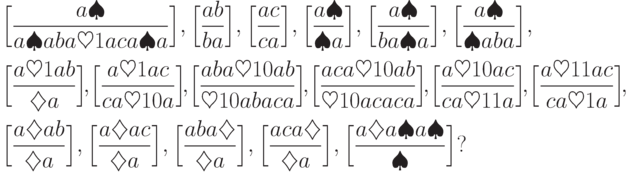
 . Тогда не существует алгоритма, позволяющего по произвольной постовской системе соответствия над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольной постовской системе соответствия над алфавитом 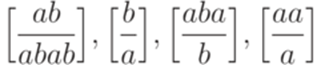 ?
?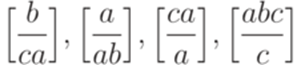 ?
?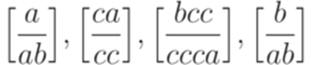 ?
?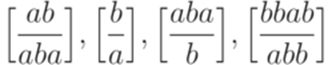 ?
?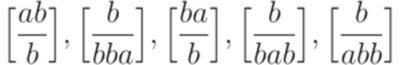 ?
?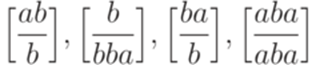 ?
?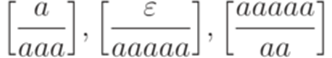 ?
?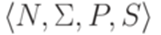 называется неукорачивающей (noncontracting), если для каждого правила
называется неукорачивающей (noncontracting), если для каждого правила 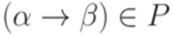 выполняется неравенство
выполняется неравенство  .
.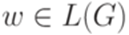 .
.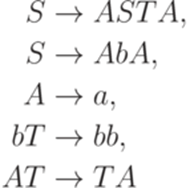
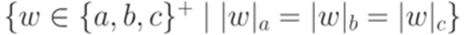 .
.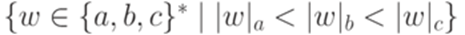 .
.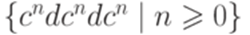 .
. .
.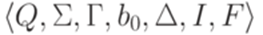
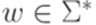 ,
, 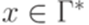 ,
,  ,
, 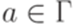 и
и  , что
, что 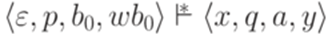 и |xay| > |b0wb0|.
и |xay| > |b0wb0|.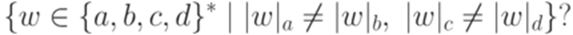
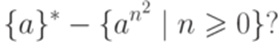
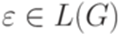 .
.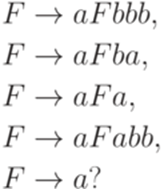
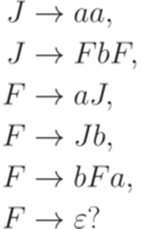
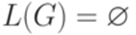 .
.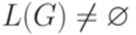 .
.