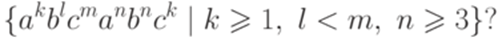Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лемма о разрастании для контекстно-свободных языков
Лемма 9.1.1 (pumping lemma, лемма о разрастании, лемма о накачке, лемма-насос) Пусть L - контекстно-свободный язык над алфавитом Доказательство. Пусть язык Положим p = 2|N|. Пусть Из того что G - грамматика в нормальной форме Хомского, заключаем, что Пример 9.1.2. Рассмотрим язык Теорема 9.1.3. Каждый контекстно-свободный язык над однобуквенным алфавитом является автоматным. Доказательство. Пусть дан контекстно-свободный язык L над алфавитом {a}. Согласно лемме 9.1.1 найдется такое натуральное число p, что множество
Упражнение 9.1.4. Является ли контекстно-свободным язык Упражнение 9.1.5. Является ли контекстно-свободным язык Упражнение 9.1.6. Является ли контекстно-свободным язык Упражнение 9.1.7. Является ли контекстно-свободным язык {am | m простое}? Упражнение 9.1.8. Является ли контекстно-свободным язык Упражнение 9.1.9. Является ли контекстно-свободным язык Упражнение 9.1.10. Является ли контекстно-свободным язык Упражнение 9.1.11. Является ли контекстно-свободным язык Упражнение 9.1.12. Является ли контекстно-свободным язык Упражнение 9.1.13. Является ли контекстно-свободным язык {akbmcn | k < max(m,n)}? Упражнение 9.1.14. Является ли контекстно-свободным язык {akbmcn | k > max(m,n)}? Упражнение 9.1.15. Является ли контекстно-свободным язык
Упражнение 9.1.16. Какому классу принадлежит язык, порождаемый грамматикой
Упражнение 9.1.17. Существуют ли такие контекстно-свободные языки
9.2*. Лемма о разрастании для линейных языков Определение 9.2.1. Линейная грамматика в нормальной форме - это такая линейная грамматика, в которой каждое правило имеет вид Теорема 9.2.2. Каждая линейная грамматика эквивалентна некоторой линейной грамматике в нормальной форме. Теорема 9.2.3. Если линейный язык не содержит пустого слова, то он порождается некоторой линейной грамматикой в нормальной форме без Теорема 9.2.4. Язык L является линейным тогда и только тогда, когда язык Лемма 9.2.5. Пусть L - линейный язык над алфавитом Доказательство. Пусть язык
Пример 9.2.6. Рассмотрим язык Упражнение 9.2.7. Какому классу принадлежит язык
Упражнение 9.2.8. Какому классу принадлежит язык
Упражнение 9.2.9. Какому классу принадлежит язык
|
||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.63.236 (0.008 с.) |
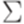 . Тогда найдется такое положительное целое число p, что для любого слова
. Тогда найдется такое положительное целое число p, что для любого слова  длины не меньше p можно подобрать слова
длины не меньше p можно подобрать слова 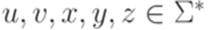 , для которых верно uvxyz = w,
, для которых верно uvxyz = w,  (то есть
(то есть  или
или 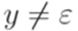 ),
), 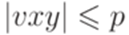 и
и 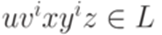 для всех
для всех 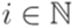 .
.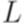 порождается грамматикой в нормальной форме Хомского
порождается грамматикой в нормальной форме Хомского 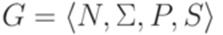 . Индукцией по k легко доказать, что для любого дерева вывода в грамматике G длина кроны дерева не превышает 2k-2, где k - количество вершин в самом длинном пути, начинающемся в корне дерева и заканчивающемся в некоторой вершине, помеченной символом из
. Индукцией по k легко доказать, что для любого дерева вывода в грамматике G длина кроны дерева не превышает 2k-2, где k - количество вершин в самом длинном пути, начинающемся в корне дерева и заканчивающемся в некоторой вершине, помеченной символом из 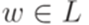 и
и  . Зафиксируем некоторое дерево вывода с кроной w в грамматике G. Рассмотрим самый длинный путь в этом дереве. Этот путь содержит не менее |N| + 2 вершин. Среди них найдутся две вершины с одинаковыми метками, причем их можно выбрать среди последних |N| + 2 вершин рассматриваемого пути. Выберем слова u, v, x, y и z так, что uvxyz = w, поддерево с корнем в одной из найденных вершин имеет крону xи поддерево с корнем в другой найденной вершине имеет крону vxy.
. Зафиксируем некоторое дерево вывода с кроной w в грамматике G. Рассмотрим самый длинный путь в этом дереве. Этот путь содержит не менее |N| + 2 вершин. Среди них найдутся две вершины с одинаковыми метками, причем их можно выбрать среди последних |N| + 2 вершин рассматриваемого пути. Выберем слова u, v, x, y и z так, что uvxyz = w, поддерево с корнем в одной из найденных вершин имеет крону xи поддерево с корнем в другой найденной вершине имеет крону vxy.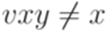 . Неравенство
. Неравенство  следует из того, что самый длинный путь в соответствующем слову vxy поддереве содержит не более |N| + 2 вершин. Для каждого
следует из того, что самый длинный путь в соответствующем слову vxy поддереве содержит не более |N| + 2 вершин. Для каждого 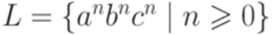 над алфавитом {a,b,c}. Утверждение леммы 9.1.1 не выполняется ни для какого натурального числа p. Действительно, если uvxyz = apbpcp, |vy| > 0 и
над алфавитом {a,b,c}. Утверждение леммы 9.1.1 не выполняется ни для какого натурального числа p. Действительно, если uvxyz = apbpcp, |vy| > 0 и 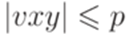 , то |vy|a = 0 или |vy|c = 0. Следовательно, |uvvxyyz|a = p или |uvvxyyz|c = p. Так как |uvvxyyz| > 3p, то
, то |vy|a = 0 или |vy|c = 0. Следовательно, |uvvxyyz|a = p или |uvvxyyz|c = p. Так как |uvvxyyz| > 3p, то  . Из этого можно заключить, что язык L не является контекстно-свободным.
. Из этого можно заключить, что язык L не является контекстно-свободным.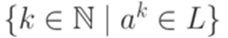 является объединением некоторого семейства арифметических прогрессий, причем у каждой прогрессии первый член и шаг не больше числа p. Так как существует лишь конечное число прогрессий натуральных чисел с таким ограничением, рассматриваемое семейство конечно. Следовательно, язык L является автоматным (используем пример 2.1.18).
является объединением некоторого семейства арифметических прогрессий, причем у каждой прогрессии первый член и шаг не больше числа p. Так как существует лишь конечное число прогрессий натуральных чисел с таким ограничением, рассматриваемое семейство конечно. Следовательно, язык L является автоматным (используем пример 2.1.18).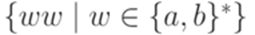 ?
?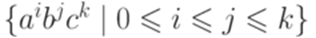 ?
? ?
?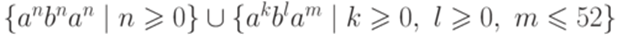 ?
? ?
?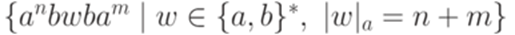 ?
? ?
? ?
?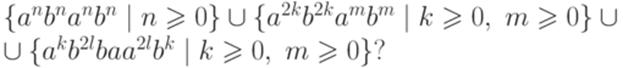

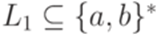 и
и  , что язык
, что язык  не является контекстно-свободным?
не является контекстно-свободным?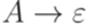 ,
, 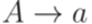 ,
,  или
или  , где
, где 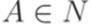 ,
, 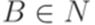 ,
, 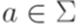 .
.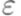 - правил.
- правил.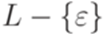 является линейным.
является линейным.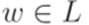 длины не меньше p можно подобрать слова
длины не меньше p можно подобрать слова 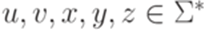 , для которых верно uvxyz = w,
, для которых верно uvxyz = w,  (то есть
(то есть  или
или 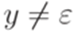 ),
), 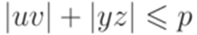 и
и 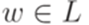 и
и 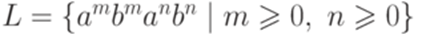 над алфавитом {a,b}. Утверждение леммы 9.2.5 не выполняется ни для какого натурального числа p. Следовательно, язык L не является линейным.
над алфавитом {a,b}. Утверждение леммы 9.2.5 не выполняется ни для какого натурального числа p. Следовательно, язык L не является линейным.