Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множества двусторонних контекстов
Определение 6.3.1. Пусть
Пример 6.3.2. Пусть
Лемма 6.3.3. Если Доказательство. Из определений следует, что
Лемма 6.3.4. Если Доказательство. Пусть Лемма 6.3.5. Если Определение 6.3.6. Пусть
называется синтаксическим моноидом (syntactic monoid) языка L. Определение 6.3.7*. Полугруппой (semigroup) Определение 6.3.8*. Пусть Определение 6.3.9*. Моноид Теорема 6.3.10*. Определим бинарную операцию на Synt(L) следующим образом:
Тогда Теорема 6.3.11. Синтаксический моноид Synt(L) конечен тогда и только тогда, когда язык L является автоматным. Доказательство Пусть множество Synt(L) конечно. Согласно лемме 6.3.3 множество Обратно, пусть язык L распознается некоторым конечным автоматом
Легко проверить, что если Пример 6.3.12. Рассмотрим конечный автомат M из примера 2.1.14. Тогда 1. 2. если 3. если 4. если 5. если 6. 7. Лемма 6.3.13. Пусть
Доказательство. Индукцией по 6.4*. Классы эквивалентности слов Лемма 6.4.1. Пусть
Определение 6.4.2. Пусть Пример 6.4.3. Пусть Пример 6.4.4. Пусть
Лемма 6.4.5. Если язык Доказательство. Пусть язык L распознается конечным автоматом
Каждый из языков [x]L и
Замечание 6.4.6. Из теоремы 6.1.8 вытекает, что если язык L автоматный, то существует лишь конечное число различных множеств Пример 6.4.7. Рассмотрим язык
над алфавитом
Теорема 6.4.11. Язык Замечание 6.4.12. Теоремы 6.1.8 и 6.4.11 образуют теорему Майхилла-Нерода. Перейдем к более богатому классу языков - к контекстно-свободным языкам. Они находят применение в разнообразных программных продуктах, таких как компиляторы, средства форматирования исходного кода, средства статического анализа программ, синтаксические редакторы, системы верстки, программы просмотра форматированного текста, поисковые системы. Начнем рассмотрение контекстно-свободных языков с введения понятия деревьев вывода, что позволит определить важное для компьютерных приложений понятие однозначности контекстно-свободной грамматики. Чтобы не вдаваться в детали определения изоморфизма ориентированных деревьев, будем использовать в определении однозначности понятие левостороннего вывода (раздел 7.2). Соответствие деревьев вывода и левосторонних (а также правосторонних) выводов понадобится также в "лекции 13". Из класса всех контекстно-свободных языков можно выделить подкласс тех языков, для которых существует хотя бы одна однозначная грамматика. В разделе 7.3* доказывается, что все праволинейные (то есть автоматные) языки принадлежат этому подклассу.
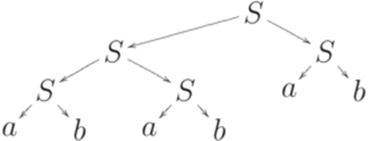
В последнем разделе этой лекции приводятся важные конкретные примеры однозначных контекстно-свободных грамматик, моделирующих системы правильно вложенных скобок и польскую (префиксную) запись выражений. Деревья вывода Определение 7.1.1. Выводам в контекстно-свободной грамматике соответствуют так называемые деревья вывода (деревья разбора, derivation tree, parse tree) - некоторые упорядоченные деревья, вершины которых помечены символами алфавита Кроной (yield) дерева вывода называется слово, записанное в вершинах, помеченных символами из алфавита Пример 7.1.2. Рассмотрим контекстно-свободную грамматику
Выводу
Крона этого дерева вывода - ababab.
|
||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.125.219 (0.012 с.) |
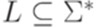 и
и  . Тогда множество контекстов (множество двусторонних контекстов) слова y относительно языка L определяется следующим образом:
. Тогда множество контекстов (множество двусторонних контекстов) слова y относительно языка L определяется следующим образом: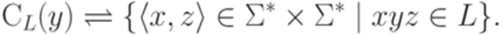
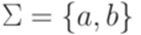 и
и 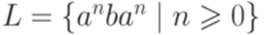 . Тогда
. Тогда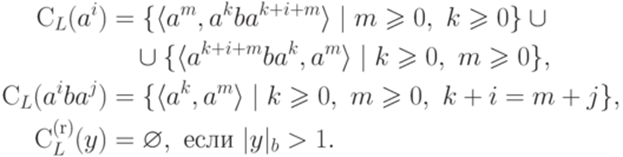
 , то
, то  .
.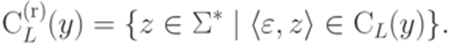
 и
и  .
.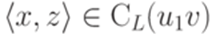 . Тогда
. Тогда 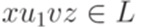 . Следовательно,
. Следовательно,  . Далее, получаем, что
. Далее, получаем, что  ,
, 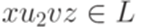 и
и 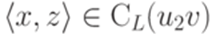 . Второе равенство доказывается аналогично.
. Второе равенство доказывается аналогично. , то
, то  .
.
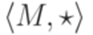 называется непустое множество M с ассоциативной бинарной операцией
называется непустое множество M с ассоциативной бинарной операцией  .
.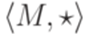 - полугруппа. Элемент
- полугруппа. Элемент 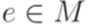 называется единицей (unit), если
называется единицей (unit), если 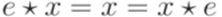 для каждого
для каждого 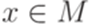 .
. - это полугруппа
- это полугруппа 
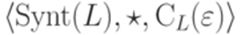 является моноидом.
является моноидом.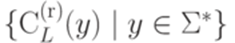 тоже конечно. В силу леммы 6.1.6 язык L является автоматным.
тоже конечно. В силу леммы 6.1.6 язык L является автоматным.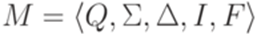 , не содержащим переходов с метками длины больше единицы. Поставим в соответствие каждому слову y множество
, не содержащим переходов с метками длины больше единицы. Поставим в соответствие каждому слову y множество 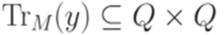 , определенное следующим образом:
, определенное следующим образом:
 , то
, то  . Следовательно,
. Следовательно, 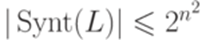 , где n = |Q|.
, где n = |Q|.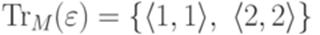 ;
; , то
, то 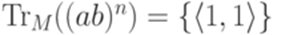 ;
;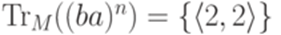 ;
; , то
, то 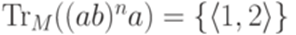 ;
;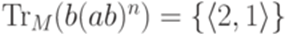 ;
; ;
; .
.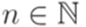 и для каждого слова
и для каждого слова 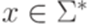 , что
, что  и
и  . Тогда
. Тогда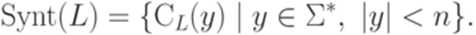
 можно доказать, что для каждого слова
можно доказать, что для каждого слова 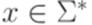 , что
, что 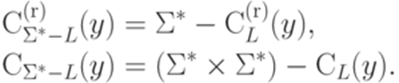
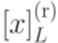 язык
язык 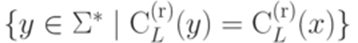 . Обозначим через
. Обозначим через 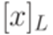 язык
язык 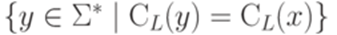 .
.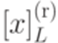 образуют разбиение множества
образуют разбиение множества 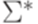 на классы эквивалентности. Множества вида
на классы эквивалентности. Множества вида 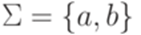 и
и 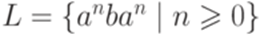 . Тогда
. Тогда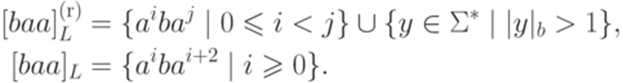
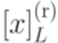 и
и 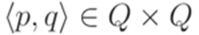 язык
язык  является автоматным (он распознается конечным автоматом
является автоматным (он распознается конечным автоматом 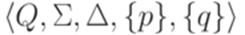 ). Для каждого слова
). Для каждого слова 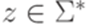 язык
язык 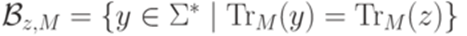 является автоматным, так как он представим в виде пересечения конечного семейства автоматных языков:
является автоматным, так как он представим в виде пересечения конечного семейства автоматных языков: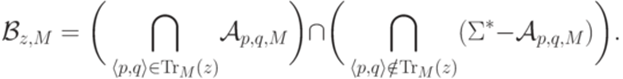
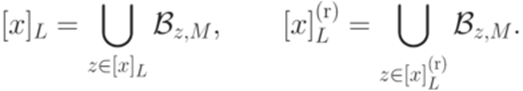
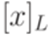 (см. теорему 6.3.11).
(см. теорему 6.3.11).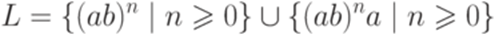
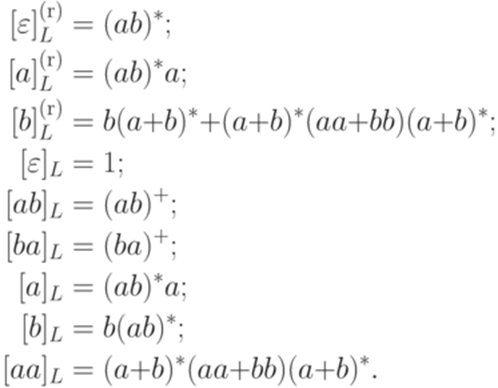
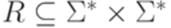 , что R разбивает
, что R разбивает  . Корень дерева отвечает начальному символу. Каждому символу слова w1, на которое заменяется начальный символ на первом шаге вывода, ставится в соответствие вершина дерева, и к ней проводится дуга из корня. Полученные таким образом непосредственные потомки корня упорядочены согласно порядку их меток в слове w1. Для тех из полученных вершин, которые помечены символами из множества N, делается аналогичное построение, и т. д.
. Корень дерева отвечает начальному символу. Каждому символу слова w1, на которое заменяется начальный символ на первом шаге вывода, ставится в соответствие вершина дерева, и к ней проводится дуга из корня. Полученные таким образом непосредственные потомки корня упорядочены согласно порядку их меток в слове w1. Для тех из полученных вершин, которые помечены символами из множества N, делается аналогичное построение, и т. д. .
.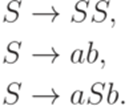
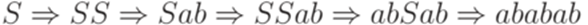 соответствует следующее дерево вывода.
соответствует следующее дерево вывода.