
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Детерминированные конечные автоматыСодержание книги
Поиск на нашем сайте Определение 2.6.1. Конечный автомат 1. множество I содержит ровно один элемент; 2. для каждого перехода 3. для любого символа Пример 2.6.2. Конечный автомат из примера 2.1.14 является детерминированным. Определение 2.6.3. Детерминированный конечный автомат Пример 2.6.4. Конечный автомат из примера 2.1.14 эквивалентен полному детерминированному конечному автомату
Замечание 2.6.5. Некоторые авторы используют в определении полного детерминированного конечного автомата вместо отношения
2.7. Преобразование конечного автомата к детерминированному виду Теорема 2.7.1 Каждый автоматный язык распознается некоторым полным детерминированным конечным автоматом. Доказательство. Без ограничения общности можно предположить, что исходный язык задан конечным автоматом
Обозначим через
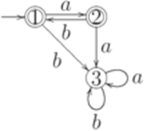
Пример 2.7.2. Пусть
Если применить конструкцию из доказательства теоремы 2.7.1. и затем удалить состояния, не достижимые из начального состояния, то получится полный детерминированный конечный автомат
где
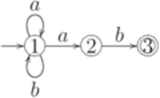
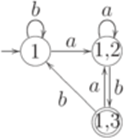
Упражнение 2.7.3. Найти полный детерминированный конечный автомат, эквивалентный автомату, изображенному на диаграмме.
Упражнение 2.7.4. Найти детерминированный конечный автомат для языка, порождаемого грамматикой
Для практического применения теории конечных автоматов нужны средства, позволяющие выяснять, является ли некоторый формальный язык автоматным. Для получения положительного ответа на такой вопрос могут пригодиться достаточные условия автоматности, для отрицательного ответа - необходимые условия автоматности. В этой лекции рассматриваются наиболее часто используемые условия, касающиеся автоматности формального языка. В первых двух разделах этой лекции доказываются свойства замкнутости класса всех автоматных языков (относительно итерации, конкатенации, объединения, дополнения, пересечения и т. д.). Эти свойства можно использовать как достаточные условия автоматности. Например, если нужно выяснить, является ли язык L автоматным, и удается представить L в виде В последних двух разделах этой лекции доказывается так называемая лемма о разрастании (в англоязычной литературе pumping lemma), которая во многих случаях позволяет установить неавтоматность формального языка. К сожалению, эта лемма помогает не всегда, так как дает всего лишь необходимое условие, а не критерий автоматности.
|
||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.005 с.) |

 называется детерминированным (deterministic), если
называется детерминированным (deterministic), если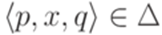 выполняется равенство |x| = 1;
выполняется равенство |x| = 1;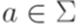 и для любого состояния
и для любого состояния  существует не более одного состояния
существует не более одного состояния  со свойством
со свойством 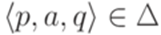 .
.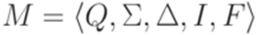 называется полным (complete), если для каждого состояния
называется полным (complete), если для каждого состояния 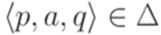 .
. , где Q = {1,2,3},
, где Q = {1,2,3}, 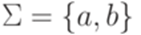 , I = {1}, F = {1,2},
, I = {1}, F = {1,2},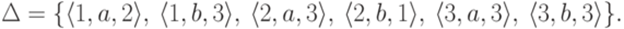
 функцию
функцию 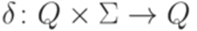 . От функции
. От функции 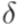 можно перейти к отношению
можно перейти к отношению 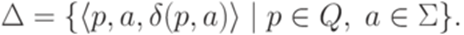
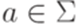 и
и 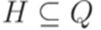 обозначим
обозначим
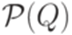 множество всех подмножеств множества Q. Построим искомый полный детерминированный конечный автомат
множество всех подмножеств множества Q. Построим искомый полный детерминированный конечный автомат 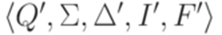 , положив
, положив 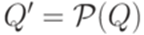 ,
,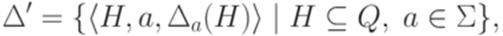
 и
и 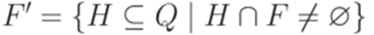 .
.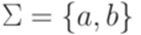 . Рассмотрим конечный автомат
. Рассмотрим конечный автомат 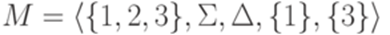 , где
, где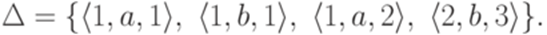
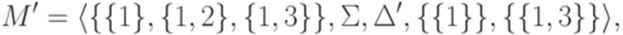
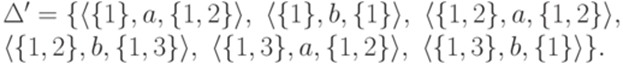
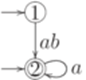
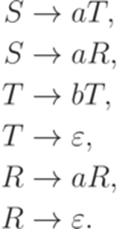
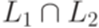 , где языки L1 и L2 автоматные, то и язык L обязательно является автоматным.
, где языки L1 и L2 автоматные, то и язык L обязательно является автоматным.


