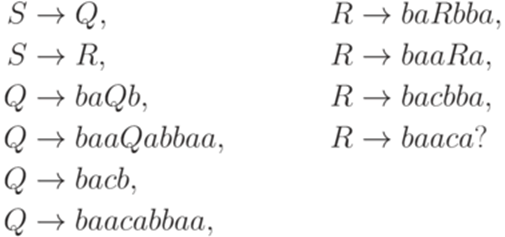Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пересечение контекстно-свободных языков
Определение 16.1.1. Рассмотрим алфавит
Обозначим через Лемма 16.1.2. Язык Пример 16.1.3. Рассмотрим постовскую систему соответствия
(то есть n = 2,
Теорема 16.1.4. Пусть Доказательство. Сначала докажем утверждение теоремы для случая Чтобы доказать утверждение теоремы для случая Лемма 16.1.5. Язык Доказательство. Если постовская система соответствия имеет хотя бы одно решение, то она имеет бесконечно много решений. Теорема 16.1.6. Пусть Упражнение 16.1.7. Пусть
и язык L2, порождаемый грамматикой
Верно ли, что Упражнение 16.1.8. Пусть
и язык
Верно ли, что Упражнение 16.1.9. Пусть
и язык L2, порождаемый грамматикой
Верно ли, что
Проблема однозначности Теорема 16.2.1. Пусть Доказательство. Рассмотрим язык
Грамматика G является неоднозначной тогда и только тогда, когда постовская система соответствия Упражнение 16.2.2. Однозначна ли контекстно-свободная грамматика
|
|||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 73; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.188.64 (0.008 с.) |
 . Пусть
. Пусть 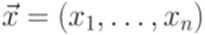 , где
, где 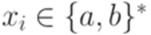 для всех i. Обозначим через
для всех i. Обозначим через 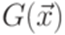 линейную грамматику
линейную грамматику 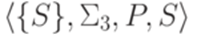 , где
, где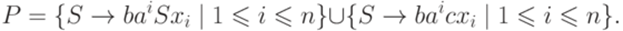
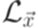 язык, порождаемый грамматикой
язык, порождаемый грамматикой 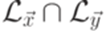 является непустым тогда и только тогда, когда постовская система соответствия
является непустым тогда и только тогда, когда постовская система соответствия 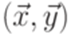 имеет решение.
имеет решение.
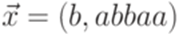 и
и  ). Решениями этой системы являются последовательности (1, 1, 2), (1, 1, 2, 1, 1, 2) и т. д. Легко убедиться, что
). Решениями этой системы являются последовательности (1, 1, 2), (1, 1, 2, 1, 1, 2) и т. д. Легко убедиться, что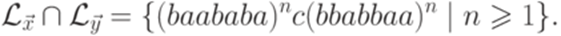
 . Тогда не существует алгоритма, позволяющего по произвольным контекстно-свободным грамматикам G1 и G2 над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольным контекстно-свободным грамматикам G1 и G2 над алфавитом 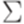 узнать, верно ли, что
узнать, верно ли, что 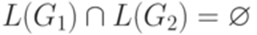 .
. . Из леммы 16.1.2 следует, что если бы проблема распознавания свойства
. Из леммы 16.1.2 следует, что если бы проблема распознавания свойства 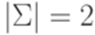 (например,
(например, 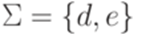 ), достаточно заменить в определении
), достаточно заменить в определении  символ a на ede, символ b на edde и символ c на eddde.
символ a на ede, символ b на edde и символ c на eddde.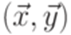 имеет решение.
имеет решение. . Тогда не существует алгоритма, позволяющего по произвольным контекстно-свободным грамматикам G1 и G2 над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольным контекстно-свободным грамматикам G1 и G2 над алфавитом 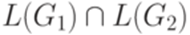 .
.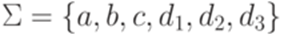 . Рассмотрим язык L1, порождаемый грамматикой
. Рассмотрим язык L1, порождаемый грамматикой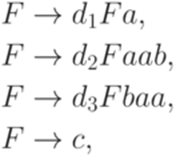
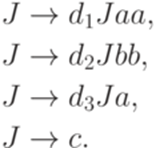
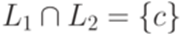 ?
?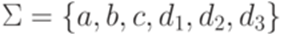 . Рассмотрим язык L1, порождаемый грамматикой
. Рассмотрим язык L1, порождаемый грамматикой
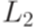 , порождаемый грамматикой
, порождаемый грамматикой
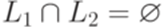 ?
?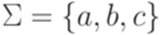 . Рассмотрим язык L1, порождаемый грамматикой
. Рассмотрим язык L1, порождаемый грамматикой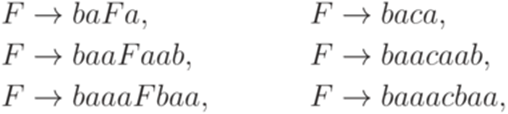

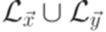 . Следуя доказательству теоремы 9.4.3, построим грамматику G для этого языка, исходя из грамматик
. Следуя доказательству теоремы 9.4.3, построим грамматику G для этого языка, исходя из грамматик 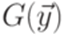 .
.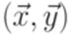 имеет решение.
имеет решение.