
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение скорости и ускорения точки по уравнениям движенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В таблицах 1, 2 заданы уравнения движения точки М и численные значения параметров к ним. Требуется установить траекторию и для момента времени t = t1 найти положение точки на ней. Вычислить скорость, полное, касательное и нормальное ускорения точки М (показать их на рисунке), радиус кривизны траектории. Заданы уравнения движения точки М:
x(t) = at; y(t) = ct2 – d (1)
Исходные данные
Решение
После подстановки численных значений уравнения (1) приобретают вид: x(t) = 4t, y(t) = 16 t2–1. (2) Чтобы получить уравнение траектории в координатной форме, исключим время t из уравнений (2). С этой целью выразим время из первого уравнения и подставим во второе:
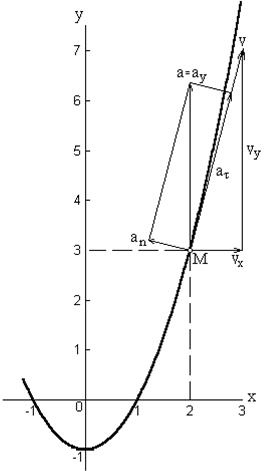
t = x / 4, y = 16 (x/4)2 – 1 = x2 – 1. Иначе x2 = y + 1 (3) Таким образом, получено уравнение параболы. Положение точки М на траектории в момент времени t1 находим по уравнениям (2): x(0,5) = 4·0,5 = 2 м, y(0,5) = 16·0,52–1 = 3 м. Для построения траектории точки, являющейся кривой линией (часть параболы), необходимо определить положения точки М ещё при нескольких моментах времени вблизи t = t1. Эти вычисления отобразим в табличной форме и построим кривую (рис.1).
Рис. 1
Вычислим проекции скорости и ускорения точки на оси координат vx, vy, ax, ay, дифференцируя по времени уравнения движения (1):
По найденным проекциям определяются модуль скорости:
и модуль ускорения точки вычисляется по формуле:
Касательное ускорение точки
Полученный знак + означает, что движение точки ускоренное, направления Модуль нормального ускорения точки определяется по формуле:
После того, как найдено нормальное ускорение, радиус кривизны траектории в рассматриваемой точке определяется из выражения:
На рисунке показано положение точки М в заданный момент времени. Вектор
Варианты заданий Таблица 1
Примечание. Единицы измерения параметров в табл. 1 соответствуют единицам измерения уравнений движения, заданных в табл. 2. Таблица 2
Некоторые формулы:
Задача К2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-04-27; просмотров: 509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.200.95 (0.01 с.) |

 ,
,  ,
, 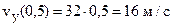 ,
,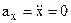 ,
, 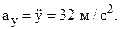
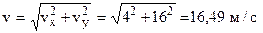

 .
. совпадают.
совпадают. .
.
 .
. строим по составляющим
строим по составляющим 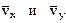 , причём этот вектор должен по направлению совпадать с касательной к траектории. Вектор
, причём этот вектор должен по направлению совпадать с касательной к траектории. Вектор  строим по составляющим
строим по составляющим 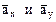 и затем раскладываем на составляющие
и затем раскладываем на составляющие  . Совпадение величин
. Совпадение величин 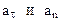 , найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.
, найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.



