Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
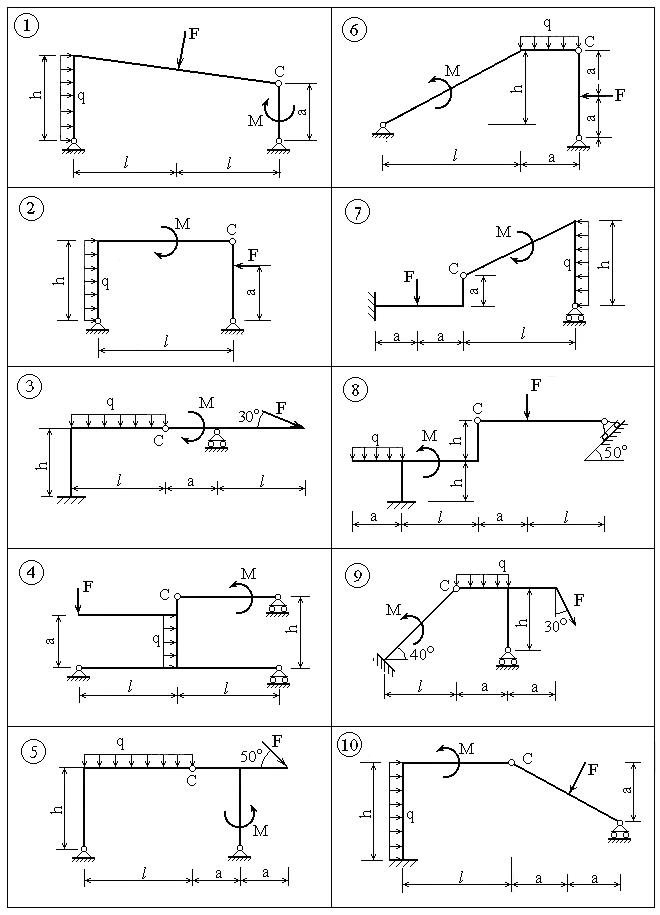
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реакции опор составной конструкции
Конструкция состоит из двух тел, соединённых с помощью шарнира C. Исходные данные берутся из таблицы. Определить реакции опор и шарнирного соединения.
Исходные данные
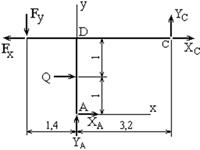
Решение Исходная схема (рис. 1) соответствует составной конструкции из двух тел, соединённых шарниром в точке С. Обозначим опоры A, B, точку D. Проведём координатные оси x и y. Шарнирно-неподвижные опоры являются внешними связями, в которых возникают по две реакции. Изобразим расчётную схему. В соответствии с принципом освобождаемости отбросим шарнирно-неподвижные опоры, и в местах их расположения приложим опорные реакции XA, YA, XB, YB (рис. 2). Образовалась изменяемая система, части которой могут поворачиваться, например, вокруг шарнира С. Однако на основании принципа отвердевания можно считать шарнир абсолютно твёрдым телом, к которому приложены заданные внешние силы и реакции связей. Внешние силы и опорные реакции образуют плоскую систему, для которой можно составить три уравнения равновесия. Между тем в них будут содержаться четыре неизвестные опорные реакции. Таким образом, условия равновесия, будучи необходимыми, не являются достаточными для определения неизвестных. Выход состоит в том, чтобы расчленить систему на две части, и для каждой из них составлять уравнения равновесия. При этом необходимо добиваться, чтобы количество уравнений соответствовало количеству неизвестных. Сначала проведём некоторые предварительные вычисления. В предстоящих выкладках удобно вместо распределённой нагрузки q иметь эквивалентную ей сосредоточенную силу Q
Составление некоторых уравнений равновесия существенно упростится, если разложить силу F на вертикальную и горизонтальную составляющие:
Наметим на рис. 2 угол α и установим его величину:
Теперь разделим рассматриваемое тело на две части: левую (рис. 3) и правую (рис. 4). В середине участка AD вместо распределённой нагрузки q отметим сосредоточенную силу Q. Вместо внешней силы F укажем их составляющие Fx, Fy; обозначенные размеры заменим их численными значениями; покажем реакции XС и YС в точке С. В последнем случае силы XС и YС, приложенные к различным частям, попарно равны по модулю, действуют вдоль одной прямой и противоположны по направлению.
Далее задача состоит в том, чтобы найти шесть неизвестных опорных реакций: XA, YA, XB, YB, XC, YC. Силы, приложенные к каждой части конструкции, образуют плоскую систему, находящуюся в равновесии, и потому удовлетворяющую трём (всего шести) уравнениям равновесия. Решение такой алгебраической системы уравнений даёт искомые реакции связей. Составим эти уравнения, одновременно производя в них числовые подстановки и простейшие преобразования. Уравнения равновесия для левой части:
Уравнения равновесия для правой части:
Анализ системы уравнений (1)–(6) показывает, что два из них, а именно (3) и (6), содержат лишь два неизвестных. Решая их как систему двух уравнений, получим:
XC = 6,98 кН, YC = 1,59 кН. Остальные неизвестные находятся легко из отдельных уравнений.
Из (1): ХА = –1,4 – XC = –1,4 – 6,98 = –8,38 кН. Из (2): YА = 5,196 – YC = 5,196 – 1,59 = 3,60 кН. Из (4): ХB = XC = 6,98 кН. Из (5): YB = YC = 1,59 кН. Реакция ХА – отрицательна, следовательно, на схеме её направление будет противоположно выбранному. Варианты заданий
Задача С3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-04-27; просмотров: 1367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.66.206 (0.006 с.) |


 = 2,2 ∙ 2,0 = 4,4 кН.
= 2,2 ∙ 2,0 = 4,4 кН.


 . (1)
. (1) . (2)
. (2) . (3)
. (3) (4)
(4) . (5)
. (5) . (6)
. (6)