Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реакции опор прямоугольной плитыСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
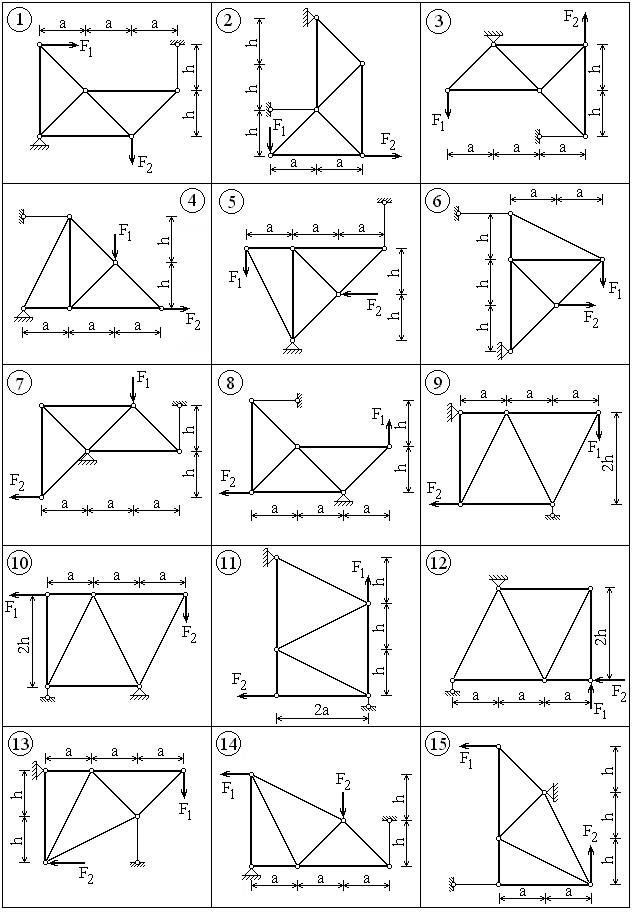
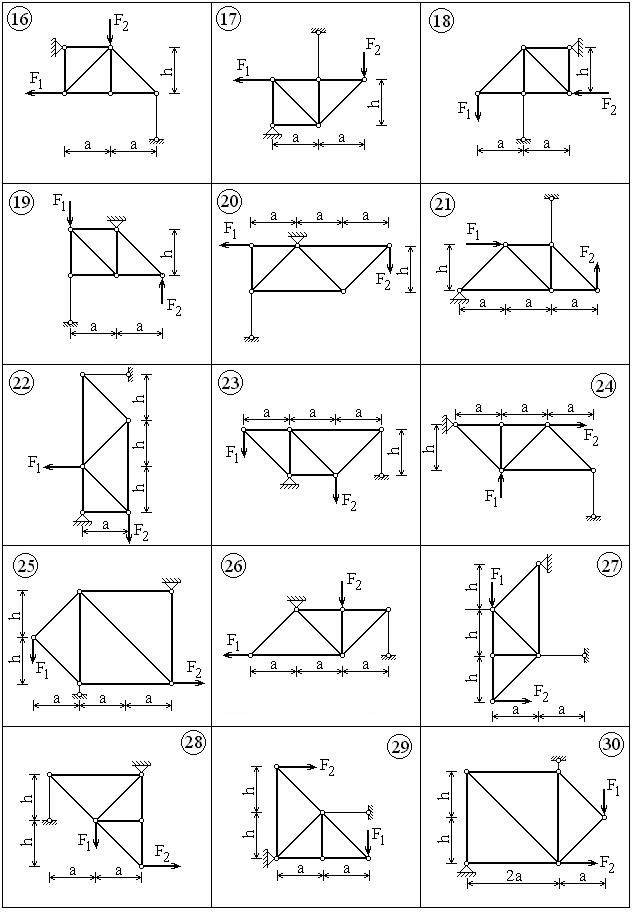
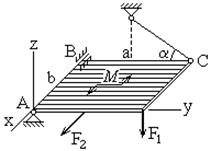
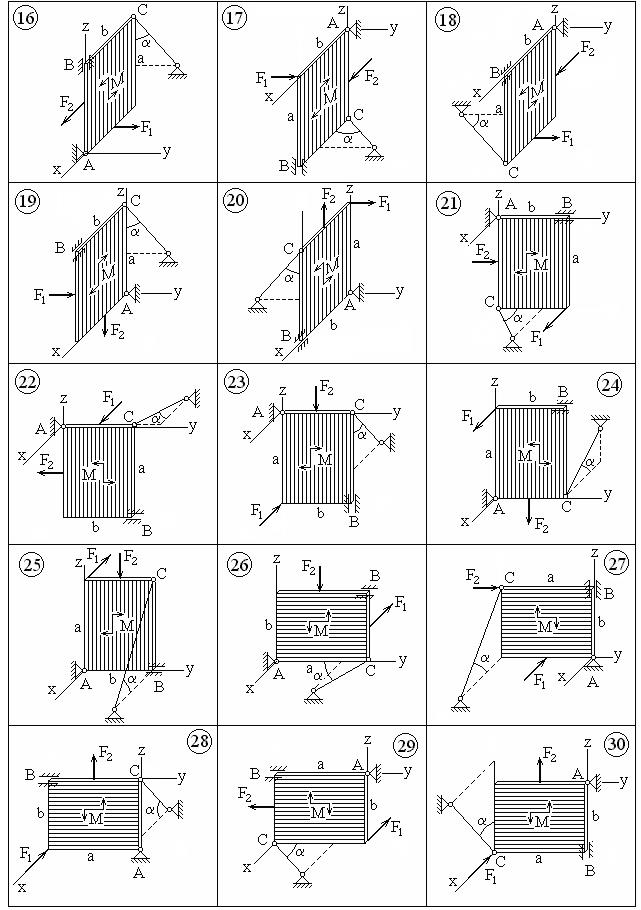
Прямоугольная однородная плита с размерами a и b закреплена с помощью трёх опор: шарнирно-неподвижной (сферический шарнир) в точке A, подшипника в точке B и опорного стержня в точке С. На плиту действуют сила тяжести G, пара сил с моментом М, сила F1, перпендикулярная к плите, сила F2, лежащая в плоскости плиты. Силы F1 и F2 приложены в серединах сторон плиты или в углах. Требуется определить реакции опор.
Исходные данные
Решение
Введём координатные оси x, y, z (рис. 1). Изобразим расчётную схему. Мысленно отбросим опоры и введём реакции (принципом освобождаемости от связей). В сферическом шарнире реакцию связей неизвестного направления разложим на составляющие по осям
Суммы моментов сил относительно координатных осей равны нулю:
Найдём опорные реакции из системы уравнений последовательно. Из (1): Из (4): Из (5): Знак минус означает, что реакция
Из (6): Из (2): Из (3):
Варианты заданий
Задача С5 Расчёт плоской фермы
Определить реакции опор и усилия в стержнях плоской фермы двумя методами: методом вырезания узлов и методом сечений. Исходные данные
Решение
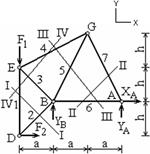
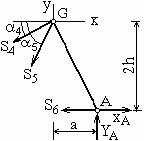
У заданной фермы (рис. 1) имеются шарнирно-неподвижная опора в точке А (две неизвестные реакции) и опорный стержень в точке В (одна неизвестная реакция). Ферма находится под действием плоской системы сил, для которой имеются три уравнения равновесия. Количество неизвестных реакций опор равно количеству уравнений. Это значит, что ферма в целом статически определима. Кроме того, должно быть соблюдено условие статической определённости в виде соотношения между количествами стержней и узлов фермы:
Количество стержней Расчёт фермы начнём с определения реакций опор. Изобразим расчётную схему (рис. 2). Покажем координатные оси х, у. По принципу освобождаемости от связей мысленно отбросим опоры и введём реакции
Отсюда находим:
Теперь приступим к определению усилий в стержнях указанными методами. 1. Метод вырезания узлов. Обозначим на расчётной схеме узлы:
Рассмотрим каждый узел. Расчёты начнём с узла, где сходятся только два стержня.
Узел D. Предполагая сходящиеся к нему стержни 1 и 2 растянутыми, изобразим узел и силы, приложенные к нему. Составим уравнения равновесия в виде равенства нулю сумм проекций сил на координатные оси x, y и находим усилия в стержнях:
Стержень 2 – сжатый.
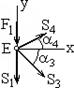
Узел Е. Аналогично составляем уравнения равновесия:
Подставим числа и получим систему двух уравнений с двумя неизвестными
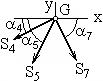
Решение даёт Стержень 3 – сжатый. Узел G. Уравнения равновесия имеют вид:
Подставляя численные значения, получим:
Решение системы даёт усилия в стержнях: Стержень 5 – сжатый. Узел A. Неизвестным является только одно усилие –
из которого находим:
Стержень 6 – сжатый. 2. Метод сечений. Проведём сечения I – I, II – II, III – III, IV – IV, пересекающие все стержни фермы. Равновесие левой части фермы в случае I – I приводит к тем же уравнениям равновесия, которые использованы выше для узла D, и поэтому их не будем рассматривать. По той же причине не рассматриваются и сечения II – II, IV – IV, которые приводят к рисункам для узлов А и Е. Очевидно, что метод сечений для усилий в стержнях 1, 2, 3, 7 даёт те же значения, которые получены выше методом вырезания узлов, ввиду полного совпадения рисунков отсечённых частей и уравнений равновесия. Изобразим правую часть фермы, отсекаемую сечением III – III. Она является частью фермы, находящейся в равновесии, и поэтому должна быть также в равновесии. Из этого следует, что уравнения равновесия для правой части должны удовлетворяться. Составим их:
Из третьего уравнения
Первое и второе уравнения образуют систему двух уравнений с двумя неизвестными
Решая её, получим: Сравнивая результаты, полученные двумя разными методами, убеждаемся, что они равны. Следовательно, решения по обоим методам являются верными.
Варианты заданий
Кинематика
Задача К1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-04-27; просмотров: 1560; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.37.74 (0.012 с.) |

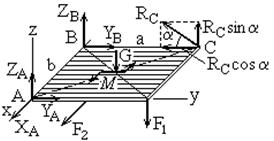
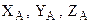 (рис. 2). Подшипник в точке В имеет только составляющие
(рис. 2). Подшипник в точке В имеет только составляющие 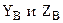 . Реакция опорного стержня
. Реакция опорного стержня 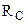 направлена по оси стержня. Её удобно для дальнейших вычислений разложить на составляющие:
направлена по оси стержня. Её удобно для дальнейших вычислений разложить на составляющие:  и
и  . Учтём также силу тяжести
. Учтём также силу тяжести 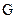 и заданные силы
и заданные силы 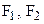 . Поскольку количество неизвестных реакций связей равно шести, и количество уравнений равновесия также шесть, система является статически определимой. Составим уравнения равновесия. Суммы проекций сил на координатные оси должны равняться нулю:
. Поскольку количество неизвестных реакций связей равно шести, и количество уравнений равновесия также шесть, система является статически определимой. Составим уравнения равновесия. Суммы проекций сил на координатные оси должны равняться нулю: . (1)
. (1)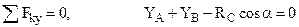 . (2)
. (2)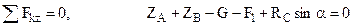 . (3)
. (3)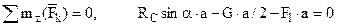 . (4)
. (4)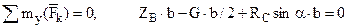 . (5)
. (5)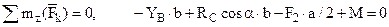 . (6)
. (6)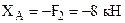 .
.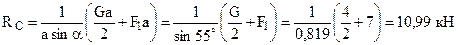 .
.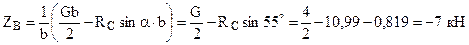 .
.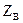 направлена противоположно показанной на рис. 2, т. е. вниз.
направлена противоположно показанной на рис. 2, т. е. вниз.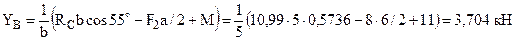 .
. .
.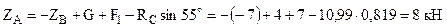 .
.

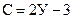 .
.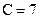 , количество узлов
, количество узлов 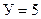 . Очевидно, что условие выполняется.
. Очевидно, что условие выполняется.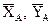 вместо шарнирно-неподвижной опоры и
вместо шарнирно-неподвижной опоры и 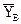 – вместо опорного стержня ВС. Для определения реакций опор рассмотрим равновесие всей фермы в целом как единого твёрдого тела. Тогда соответствующие уравнения равновесия плоской системы сил принимают вид:
– вместо опорного стержня ВС. Для определения реакций опор рассмотрим равновесие всей фермы в целом как единого твёрдого тела. Тогда соответствующие уравнения равновесия плоской системы сил принимают вид: . (1)
. (1) . (2)
. (2) . (3)
. (3)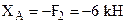 (направлена влево);
(направлена влево);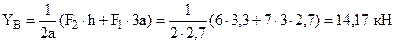 (направлена вверх);
(направлена вверх);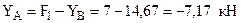 (направлена вниз).
(направлена вниз).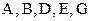 и стержни: 1, 2, 3, 4, 5, 6, 7. Далее в расчётах понадобятся углы наклона стержней к координатным осям. Найдём углы наклона к оси х-ов.
и стержни: 1, 2, 3, 4, 5, 6, 7. Далее в расчётах понадобятся углы наклона стержней к координатным осям. Найдём углы наклона к оси х-ов. ;
;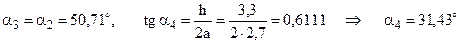 ;
;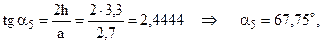
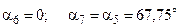 .
.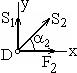
 .
.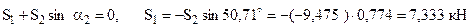 .
.
 ,
,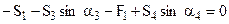 .
.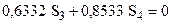 ,
, .
.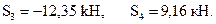
 ,
,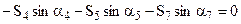 .
.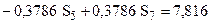 ,
,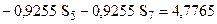 .
.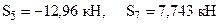 .
.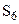 . Поэтому составляется только одно уравнение равновесия:
. Поэтому составляется только одно уравнение равновесия:
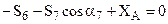 ,
,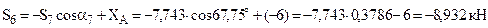 .
.
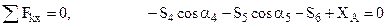 ,
,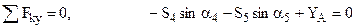 ,
,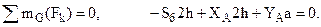
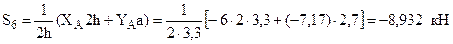 .
.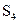 и
и 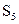 , которая после подстановки чисел имеет вид
, которая после подстановки чисел имеет вид
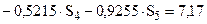 .
. .
.