Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скорости и ускорения в плоском механизме ⇐ ПредыдущаяСтр 6 из 6
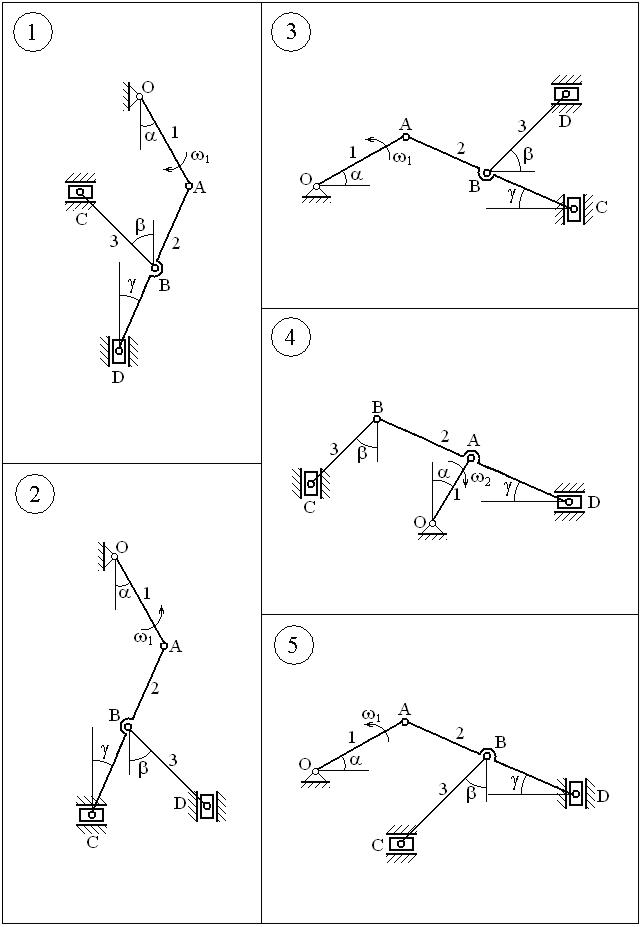
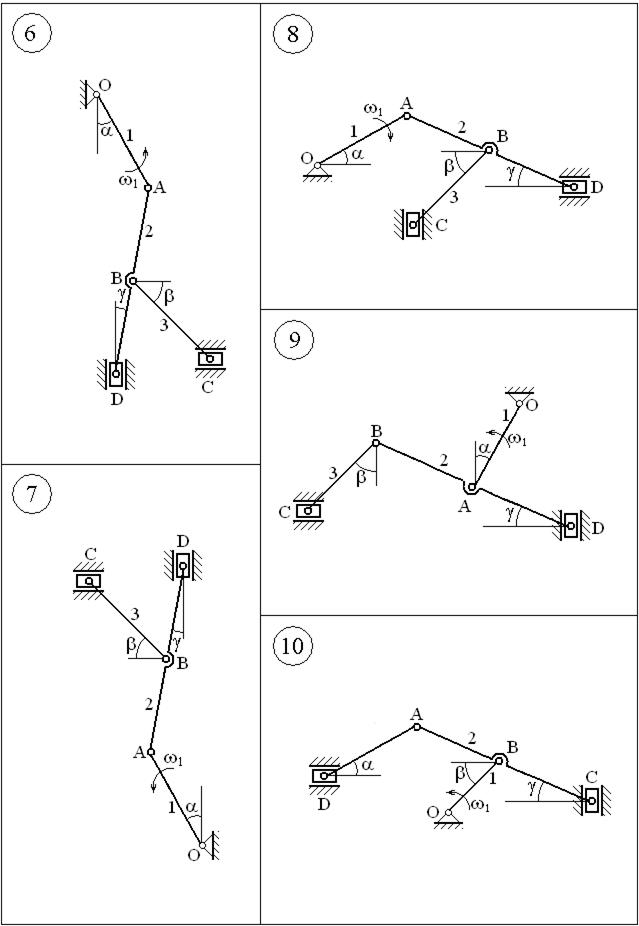
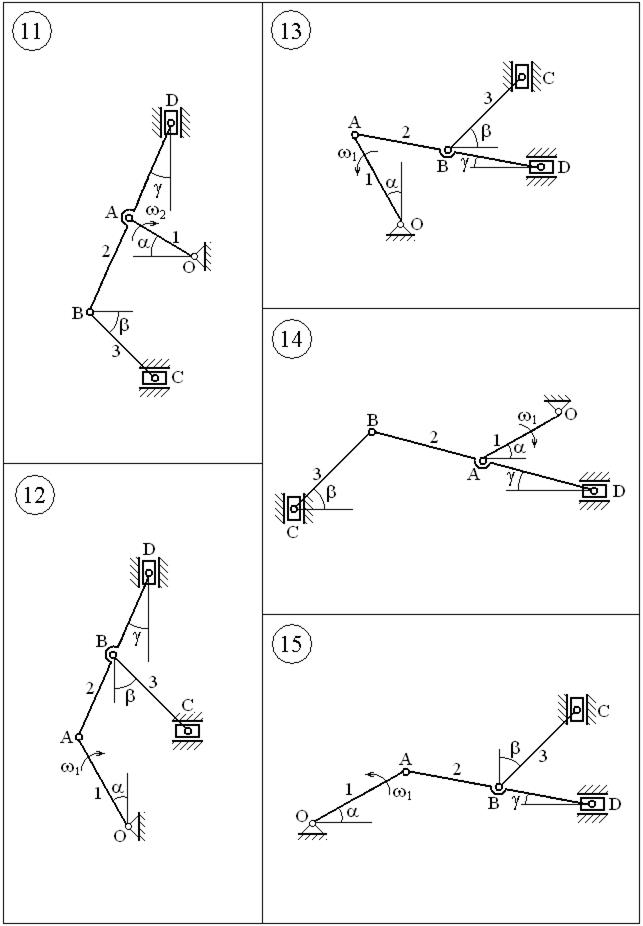
Плоский механизм состоит из стержней 1, 2, 3, двух ползунов, неподвижной опоры и двух шарниров Требуется найти: 1. Скорости точек A, B, C, D механизма; 2. Угловые скорости 3. Ускорения точек A, B, C, D; 4. Угловое ускорение Исходные данные
Решение 1. Определение скоростей точек A, B, C, D и угловых скоростей механизма. Рассмотрение механизма (рис.1) начнём с ведущего звена 1. Оно совершает вращательное движение вокруг неподвижного центра О. Определим скорость точки А кривошипа, которая одновременно принадлежит следующему звену 2
Вектор скорости Звено 2 совершает плоскопараллельное движение. Скорость точки А этого звена известна. Скорость
Расчётная схема
Далее перейдём к определению скоростей точек B и D. Проведём медиану ВЕ треугольника ADE. Определим расстояния этих точек до центра мгновенных скоростей. Известны сторона AD и два прилегающих угла
Здесь
Скорость точки В перпендикулярна отрезку ВЕ. Звено 2 (стержень AD) находится во вращательном движении относительно мгновенного центра скоростей Е. Поэтому
Отсюда получим угловую скорость
Теперь можно найти скорости точек B и D
Звено 3 (стержень ВС) совершает плоскопараллельное движение с мгновенным центром скоростей в точке F, полученной при пересечении перпендикуляров к скоростям Из треугольника BDE, все стороны которого известны, найдём угол
Отсюда
В треугольнике BCF значения углов
Таким образом, в треугольнике известны сторона и два прилежащих угла
Угловую скорость звена 3 найдём с помощью мгновенного центра скоростей из соотношения
Очевидно, что
Теперь
2. Определение ускорений точек A, B, C, D. Кривошип ОА вращается равномерно. Поэтому ускорение точки А направлено к центру О и равно нормальному ускорению
Для определения ускорения точки D звена 2 воспользуемся теоремой об ускорениях точек плоской фигуры. Считая точку А полюсом, получим
Нормальное ускорение точки D во вращательном движении вокруг полюса А направлено от точки D к точке А вдоль АD и равно
Ускорения в точке D изобразим на рис. 2. При этом направления векторов Выберем координатные оси х, y и перепишем векторное уравнение (1) в координатной форме
Решая систему уравнений (2) относительно неизвестных
Знаки минус показывают, что направления ускорений противоположны изображённым на рис. 2. Угловое ускорение стержня 2 определяется по формуле
Направление ускорения Для определения ускорения точки В примем за полюс точку А и в соответствии с теоремой об ускорениях точек плоской фигуры запишем равенство (рис.3)
Направление вектора ускорения
Вектор Для определения компонентов ускорения точки В уравнение (3) перепишем в координатной форме и вычислим (рис. 3)
Найдём величину вектора ускорения точки В по формуле
Вектор ускорения
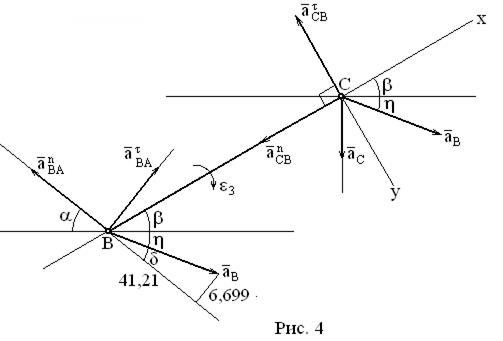
Для определения ускорения точки С примем за полюс точку В и запишем с помощью теоремы об ускорениях точек плоской фигуры (рис. 4)
Нормальное ускорение точки C во вращательном движении вокруг полюса B направлено от точки C вдоль BC и равно
Выберем координатные оси x, y и перепишем векторное уравнение (4) в координатной форме
Здесь Решая систему уравнений (5) относительно неизвестных
Знак минус показывает, что направление ускорения противоположно, изображённому на рис. 4. Угловое ускорение звена 3 определяется по формуле
Направление углового ускорения
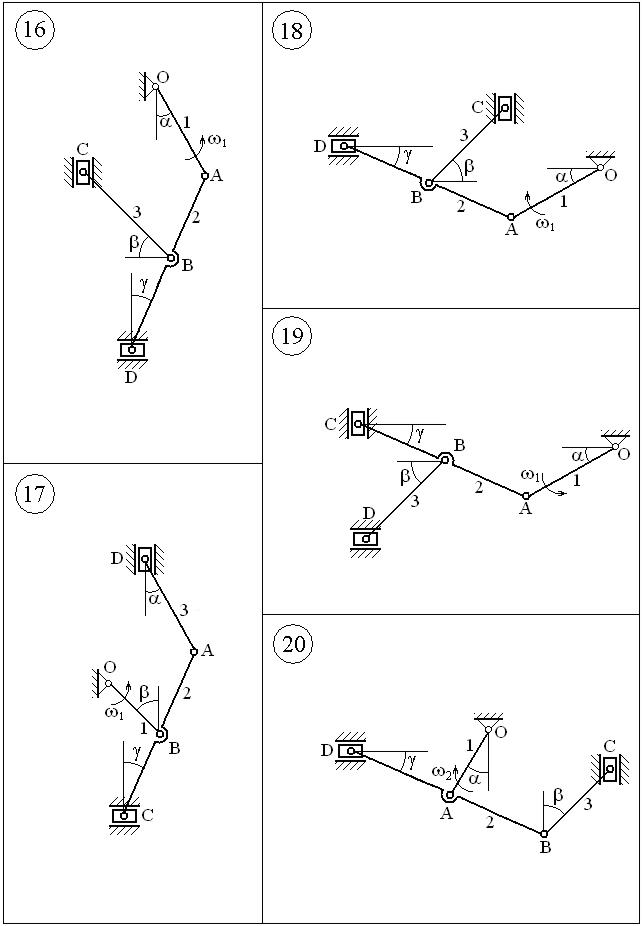
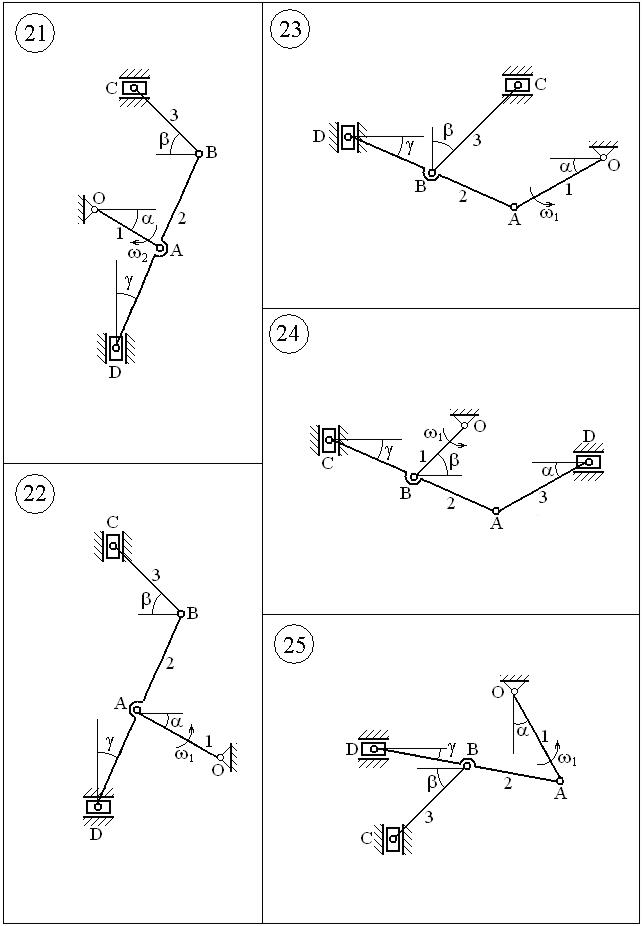
ВАРИАНТЫ ЗАДАНИЙ
Литература
1. Цывильский В.Л. Теоретическая механика. – М.: Высшая школа, 2004. 2. Теоретическая механика: методические указания и контрольные задания для студентов-заочников машиностроительных, строительных, транспортных, приборостроительных специальностей высших учебных заведений. Издание 4-е / под ред. проф. С.М. Тарга. – М.: Высшая школа, 1989. – 111 с. 3. Тарг С.М. Краткий курс теоретической механики. -М.: Высшая школа, 2004 4.Диевский В.А. Теоретическая механика. Учебное пособие. – СПб.: Изд-во «Лань», 2009.–320с. 5.Диевский В.А., Малышева И.А. Теоретическая механика. Сборник заданий: Учебное пособие. – СПб.: Изд-во «Лань», 2009. –192 с.
Содержание
ПРЕДИСЛОВИЕ.. 3 ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ РАБОТ. 3 статика Задача С1. Определение реакций опор твёрдого тела. 6 Задача С2. Определение реакций опор составной конструкции. 10 Задача С3. Определение реакций опор пространственного бруса. 16 Задача С4. Определение реакций опор прямоугольной плиты.. 20 Задача С5. Расчёт плоской фермы.. 24 КИНЕМАТИКА Задача К1. Определение скорости и ускорения точки по уравнениям движения. 29 Задача К2. Определение скоростей и ускорений точек в передаточных механизмах. 33 Задача К3. Определение скоростей и ускорений точек в планетарных механизмах. 38 Задача К4. Определение скоростей и ускорений в плоском механизме…………………….43 ЛИТЕРАТУРА.. 54
УЧЕБНОЕ ИЗДАНИЕ
Барагунова Лялюся Адальбиевна
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА СТАТИКА, КИНЕМАТИКА
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-04-27; просмотров: 639; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.122.195 (0.024 с.) |
 , соединяющих стержни. Один из шарниров располагается в середине стержня 2. Кривошип
, соединяющих стержни. Один из шарниров располагается в середине стержня 2. Кривошип 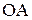 вращается равномерно с угловой скоростью
вращается равномерно с угловой скоростью 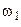 . Заданы длины стержней
. Заданы длины стержней  , углы
, углы  , угловая скорость
, угловая скорость  стержня 1.
стержня 1. ;
;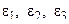 .
.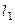 см
см
 см
см
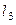 см
см
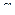 град.
град.
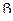 град.
град.
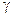 град.
град.

 .
. перпендикулярен прямой ОА и направлен в сторону вращения кривошипа, указанную дуговой стрелкой
перпендикулярен прямой ОА и направлен в сторону вращения кривошипа, указанную дуговой стрелкой  точки D горизонтальная, но неизвестна по величине. Покажем её на рисунке. Для вычисления скорости точки В требуется определить положение мгновенного центра скоростей. С этой целью проводим перпендикуляры к скоростям
точки D горизонтальная, но неизвестна по величине. Покажем её на рисунке. Для вычисления скорости точки В требуется определить положение мгновенного центра скоростей. С этой целью проводим перпендикуляры к скоростям  и
и 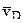 . Точка их пересечения Е является мгновенным центром скоростей.
. Точка их пересечения Е является мгновенным центром скоростей.
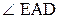 и
и 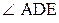 . Тогда, учитывая известные формулы для треугольников, получим
. Тогда, учитывая известные формулы для треугольников, получим ,
, .
. . Медиана BE вычисляется по соответствующей формуле
. Медиана BE вычисляется по соответствующей формуле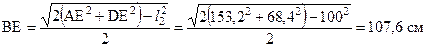 .
.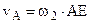 .
. звена 2 механизма
звена 2 механизма .
.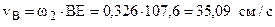 ,
, .
.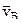 и
и  . Образовался треугольник BCF, размеры которого необходимо вычислить.
. Образовался треугольник BCF, размеры которого необходимо вычислить.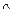 . По теореме косинусов для треугольника имеем
. По теореме косинусов для треугольника имеем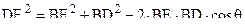 .
. ,
, 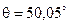 .
. ,
, .
. , и можно вычислить неизвестные стороны
, и можно вычислить неизвестные стороны ,
,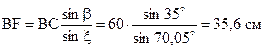 .
. .
. .
.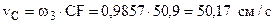 .
. .
.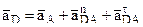 . (1)
. (1)
 .
.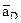 и
и  выбраны произвольно. Знак в ответе по их вычислению укажет на истинные направления.
выбраны произвольно. Знак в ответе по их вычислению укажет на истинные направления.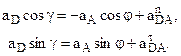 (2)
(2) и
и 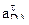 , получим
, получим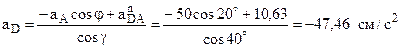 ,
,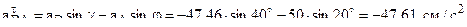 .
.
 .
.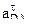 относительно полюса А определяет направление углового ускорения
относительно полюса А определяет направление углового ускорения  , которое показано на рис. 1 дуговой стрелкой.
, которое показано на рис. 1 дуговой стрелкой.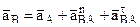 . (3)
. (3)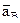 точки В заранее неизвестно. Нормальное и тангенциальное ускорения точки В во вращательном движении вокруг полюса А
точки В заранее неизвестно. Нормальное и тангенциальное ускорения точки В во вращательном движении вокруг полюса А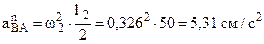 ,
,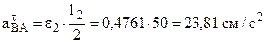 .
.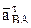 перпендикулярен вектору
перпендикулярен вектору  и направлен соответственно угловому ускорению
и направлен соответственно угловому ускорению  .
.
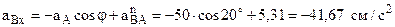 ,
,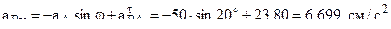 .
. .
. показан на рис. 3. Он наклонён к оси x-ов под углом
показан на рис. 3. Он наклонён к оси x-ов под углом  .
.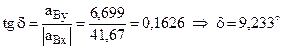 .
.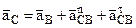 . (4)
. (4) .
. (5)
(5)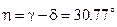 .
. и
и  получим
получим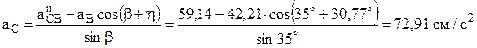 ,
,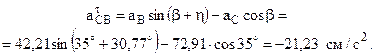
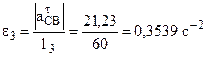 .
. определяется по тангенциальному ускорению
определяется по тангенциальному ускорению  и показано на рис. 4.
и показано на рис. 4.