
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
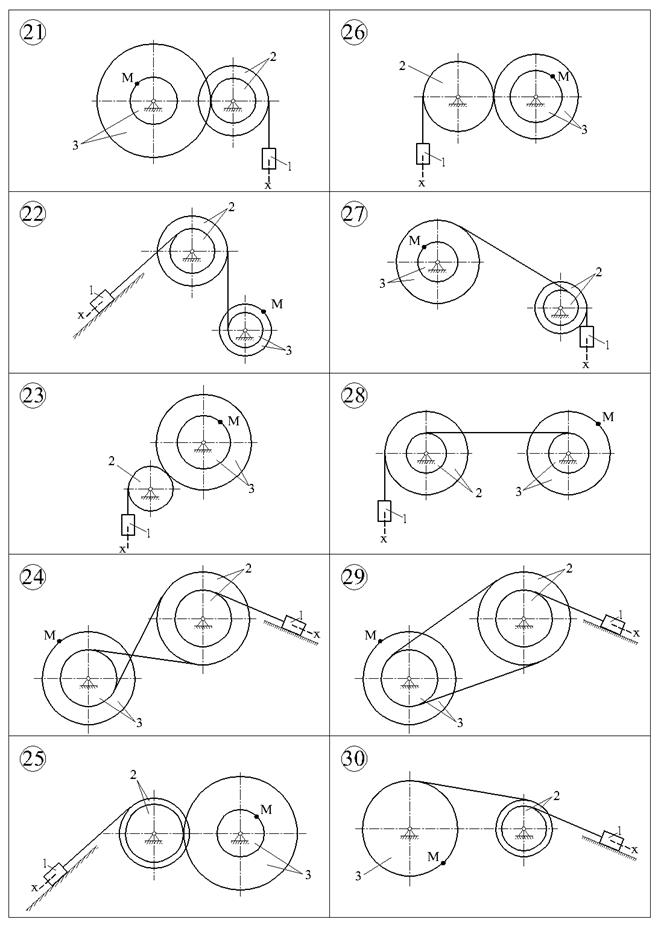
Скорости и ускорения точек в передаточных механизмах
Движение груза 1 в механизме на рис. 1 описывается уравнением
где c0, c1, c2 – некоторые постоянные, t – время в секундах. В начальный момент времени (t = 0) координата груза – x0, его скорость – v0. Координата груза в момент времени t = t2 равна x2. Определить коэффициенты Расчётная схема
Рис. 1
Исходные данные R2 = 50 cм, r2 = 25 см, R3 = 65 cм, r3 = 40 см, х0 = 14 см, v0 = 5 см/с, х2 = 168 см, t1 = 1 с, t2 = 2 с. Решение
Уравнение движения груза 1 имеет вид (1), и его коэффициенты
при при t = Скорость груза 1
Подставим (2) и (3) в формулы (1) и (4) и получим: 14 = с0, 168 = с2 ·22 + с1 · 2 + 14, 5 = с1. Отсюда легко находим
Таким образом, уравнение движения груза 1:
Скорость груза 1
Ускорение груза 1
Для определения скорости и ускорения точки М запишем уравнения, связывающие скорость груза v и угловые скорости колес ω2 и ω3. В соответствии со схемой механизма
Отсюда
или с учётом (5) после подстановки данных
В момент времени t1 ω3 = 2,215 · 1 +0,154 =2,369 рад/с. Угловое ускорение колеса 3
Определим скорость точки М, её касательное, нормальное и полное ускорения:
Рис. 2
an = r3 ω aτ = r3 ε3 =40·2,215 = 88,6 см/с2;
Скорости и ускорения тела 1 и точки М показаны на рис. 2. Варианты заданий
Задача К3 Скорости и ускорения точек в планетарных механизмах
В планетарном механизме шестерня 1 радиуса R неподвижна, а кривошип ОА, вращаясь вокруг неподвижной оси, проходящей через точку О перпендикулярно плоскости рисунка, приводит в движение свободно насаженную на конец А шестерню 2 радиусом r. Для указанного положения механизма требуется найти скорости и ускорения точек А и В, если для соответствующего момента времени известны абсолютные величины угловой скорости и углового ускорения кривошипа
Рисунок
Исходные данные
Решение Рассмотрим последовательно движения каждого из двух подвижных звеньев планетарного механизма. Начинать при этом необходимо со звена, угловая скорость и угловое ускорение которого заданы. Таким образом, начнём исследование кинематики механизма с кривошипа. 1. Кривошип ОА совершает вращательное движение вокруг неподвижной оси, проходящей через точку О перпендикулярно плоскости рисунка. Определим скорость и ускорение точки А кривошипа, которая одновременно принадлежит и подвижной шестерне 2. Абсолютная величина скорости точки А определяется по формуле:
Для заданного положения механизма
Вектор скорости Ускорение точки А представим разложенным на касательную и нормальную составляющие
Величины нормального и касательного ускорений определяются соответственно по формулам:
Для заданного положения механизма
При этом нормальное ускорение направлено по радиусу окружности, с центром в точке О. Касательное ускорение
Величина ускорения точки А в соответствии с соотношением (3) и с учётом (6) и (7) для заданного положения механизма определится по формуле:
2. Шестерня 2 совершает плоскопараллельное (плоское) движение. Шестерня 2 катится без скольжения по неподвижной шестерне 1, поэтому мгновенный центр скоростей (Р) подвижной шестерни будет находиться в точке соприкосновения двух шестерен (рисунок). Для заданного положения планетарного механизма выше определена скорость центра шестерни 2 (точки А). Таким образом, зная величину скорости одной из точек и положение мгновенного центра скоростей подвижной шестерни, можно определить величину её мгновенной угловой скорости (ω2) по формуле:
где расстояние В результате подстановки значения
Для заданного положения механизма
Направление мгновенного вращения шестерни 2 вокруг мгновенного центра скоростей Р, определяемое направлением скорости Шестерня 2 в указанном положении движется замедленно. Это следует из сопоставления направлений векторов Величину углового ускорения ε2 определим по формуле:
Учитывая (8), на основании (10) получим:
Для заданного положения механизма
Таким образом, для некоторого момента времени найдены положение мгновенного центра скоростей, угловая скорость, угловое ускорение подвижной шестерни 2, а также ускорение точки А. это позволяет найти скорость и ускорение любой точки шестерни. Прежде всего определим абсолютную величину скорости точки В по формуле:
где ВР – расстояние от точки В до мгновенного центра скоростей. Определим его из треугольника АВР. Этот треугольник равносторонний и, следовательно,
Для заданного положения механизма, учитывая (9) и (14), на основании (13) получим:
Вектор скорости
где
Величины нормального и касательного ускорений точки В при относительном вращательном движении шестерни 2 вокруг полюса А определяются по формулам:
Для заданного положения механизма на основании (18) и (19) с учётом (9) и (12) получим:
При этом нормальное ускорение Таким образом, найдены модули четырёх векторов ускорений, стоящих в правой части векторного равенства (17), и показаны их направления в точке В. По рисунку найдём ускорение точки В как геометрическую сумму четырёх показанных в точке ускорений аналитическим способом. Для этого спроектируем векторы, стоящие в правой и левой части равенства (17), на две оси координат х, у (рисунок):
Учитывая (6), (7), (20) и (21), на основании (22) и (23) найдём для заданного положения механизма проекции ускорения точки В на оси х, у:
Проекции вектора ускорения
Варианты заданий
Задача К4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-04-27; просмотров: 843; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.141.6 (0.032 с.) |
 , (1)
, (1) , при которых осуществляется требуемое движение груза 1; определить в момент времени t = t1 скорость и ускорение груза и точки M одного из колёс механизма.
, при которых осуществляется требуемое движение груза 1; определить в момент времени t = t1 скорость и ускорение груза и точки M одного из колёс механизма.
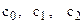 могут быть определены из следующих условий:
могут быть определены из следующих условий: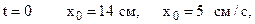 (2)
(2) (3)
(3) . (4)
. (4)
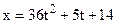 .
. . (5)
. (5)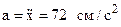 .
. .
.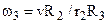 ,
,



 см/с;
см/с; =40·2,3692 = 224,5 см/с2;
=40·2,3692 = 224,5 см/с2;


 . На рисунке условно показаны направления угловой скорости и углового ускорения дуговыми стрелками вокруг оси вращения. При этом направление угловой скорости соответствует направлению вращательного движения кривошипа. Угловое ускорение направлено в сторону угловой скорости при ускоренном вращении и в противоположную – при замедленном.
. На рисунке условно показаны направления угловой скорости и углового ускорения дуговыми стрелками вокруг оси вращения. При этом направление угловой скорости соответствует направлению вращательного движения кривошипа. Угловое ускорение направлено в сторону угловой скорости при ускоренном вращении и в противоположную – при замедленном.
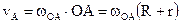 . (1)
. (1) . (2)
. (2) направлен перпендикулярно ОА (радиусу вращения) в направлении вращения, указанному на рисунке дуговой стрелкой
направлен перпендикулярно ОА (радиусу вращения) в направлении вращения, указанному на рисунке дуговой стрелкой  .
. . (3)
. (3) , (4)
, (4) . (5)
. (5) , (6)
, (6) . (7)
. (7) направлено по касательной к этой окружности (перпендикулярно ОА) в сторону, указанную дуговой стрелкой
направлено по касательной к этой окружности (перпендикулярно ОА) в сторону, указанную дуговой стрелкой  . Это объясняется тем, что при замедленном вращении (по условию задачи кривошип ОА вращается замедленно), касательное ускорение направляется в сторону, противоположную направлению вращения, указанного дуговой стрелкой
. Это объясняется тем, что при замедленном вращении (по условию задачи кривошип ОА вращается замедленно), касательное ускорение направляется в сторону, противоположную направлению вращения, указанного дуговой стрелкой  .
.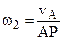 , (7)
, (7)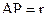 .
. и (1) в соотношение (7) получим:
и (1) в соотношение (7) получим: . (8)
. (8) . (9)
. (9)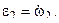 (10)
(10) , (11)
, (11) . (12)
. (12) , (13)
, (13) . (14)
. (14) . (15)
. (15) направлен перпендикулярно прямой ВР. Ускорение точки В можно найти на основании теоремы об ускорениях точек плоской фигуры, приняв точку А за полюс:
направлен перпендикулярно прямой ВР. Ускорение точки В можно найти на основании теоремы об ускорениях точек плоской фигуры, приняв точку А за полюс: , (16)
, (16) и
и  – соответственно нормальное и касательное ускорения точки В при относительном вращательном движении шестерни 2 вокруг полюса А. Учитывая (3), формулу (16) представим в виде:
– соответственно нормальное и касательное ускорения точки В при относительном вращательном движении шестерни 2 вокруг полюса А. Учитывая (3), формулу (16) представим в виде: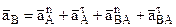 . (17)
. (17)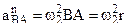 , (18)
, (18) . (19)
. (19) , (20)
, (20) . (21)
. (21) направлено вдоль ВА к центру относительного вращения (к полюсу А), а касательное ускорение
направлено вдоль ВА к центру относительного вращения (к полюсу А), а касательное ускорение  направлено перпендикулярно прямой АВ в сторону, указанную дуговой стрелкой ε2.
направлено перпендикулярно прямой АВ в сторону, указанную дуговой стрелкой ε2. , (22)
, (22) . (23)
. (23)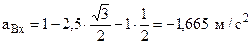 ,
,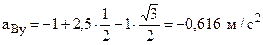 .
.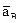 (лежащего в плоскости ху) на две оси координат полностью определяют его модуль и направление. Итак, величина
(лежащего в плоскости ху) на две оси координат полностью определяют его модуль и направление. Итак, величина .
.




