Условия головоломки следующие.

На левом берегу реки находятся три миссионера и три каннибала. К этому же берегу причалена единственная лодка. На этой лодке нужно переправить всех миссионеров и всех каннибалов на правый берег при условии, что лодка одновременно может перевозить не более двоих, в обратный путь на лодке должен отправиться хотя бы один человек. Таким образом, дозволены следующие варианты шагов (переправ):

К-> одного каннибала с левого берега на правый

КК-> двух каннибалов с левого берега на правый

МК-> одного миссионера и одного каннибала с левого берега на правый

ММ-> двух миссионеров с левого берега на правый

М-> одного миссионера с левого берега на правый

К этому нужно добавить такие же варианты переправы с правого берега на левый. Но есть еще одно обстоятельство, существенно влияющее на весь процесс: если окажется, что каннибалов на любом из берегов больше, чем миссионеров, то несчастных просто съедят. Решение головоломки — это последовательность шагов с учетом описанных ограничений, переводящая систему в заданное конечное состояние.

Конечно, эту головоломку можно решить и простым перебором и испытанием всех возможных состояний, поскольку пространство поиска не так уж велико. На рис. 2.7 показано, как образуется пространство поиска рекурсивным применением дозволенных операторов, причем на графе состояний особо выделены узлы, приводящие к образованию петель, и узлы, соответствующие недозволенным состояниям (когда кто-либо из миссионеров обречен).

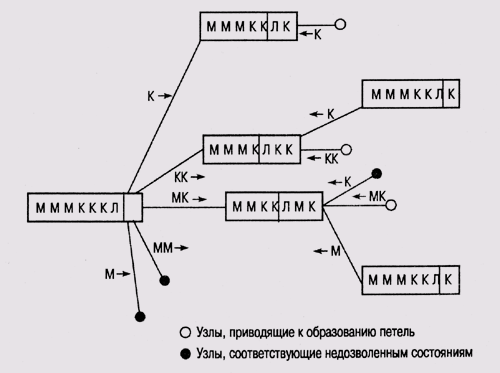
Рис. 2.7. Построение пространства поиска в головоломке "миссионеры и каннибалы"

На рис. 2.8 показано законченное пространство поиска, сформированное алгоритмом поиска в глубину, причем перебор возможных шагов ведется в том порядке, в котором они перечислены в представленном в условии, списке.

Рис. 2.8. Законченное пространство поиска в головоломке "миссионеры и каннибалы ", сформированное алгоритмом поиска в глубину

В процессе поиска было развернуто 22 узла, а путь, приводящий к успеху, содержит 11 узлов. Таким образом, оценка проницательности поиска равна 11/22=0.5. Грубо говоря, проницательность поиска говорит нам о том, насколько данный алгоритм позволил избежать выполнения ненужной работы в процессе Поиска решения. Чем выше значение проницательности поиска для того или иного алгоритма, тем лучше.

I) Выберите представление состояний на берегах реки и разработайте программу, которая решает эту задачу, используя оба варианта алгоритмов поиска— в глубину и в ширину. С разными способами формализации этой

задачи можно познакомиться в работе Амарела [Amarel, 1968]. Обратите внимание на то, что существуют способы представления состояний, которые позволяют более экономно использовать вычислительные ресурсы при решении задачи.

II) Попытайтесь улучшить оценку проницательности поиска, полученную для алгоритма поиска в глубину (рис. 2.8), изменив порядок, в котором анализируются в каждом очередном состоянии дозволенные операторы.

III) Обобщите программу как в части количества пассажиров в лодке, так и в части количества миссионеров/каннибалов. Сделайте их параметрами программы, задаваемыми извне. Если вы начнете проводить эксперименты с такой программой, то убедитесь, что, во-первых, эти параметры нельзя варьировать независимо, поскольку при некоторых комбинациях задача не имеет решения, а во-вторых, увеличение значений любого из параметров существенно расширяет пространство поиска.

7. Другая классическая головоломка, знакомая в несколько ином виде многим еще со школьной скамьи, — "Восьмерка". В головоломке принимает участие восемь пронумерованных фишек, которые могут перемещаться по игровому полю 3x3. Цель состоит в том, чтобы из некоторого случайного расположения фишек перейти к упорядоченному (рис. 2.9).

Мы несколько модифицируем ограничения, сформулировав их в терминах перемещения единственного "пустого поля".

Рис. 2.9. Головоломка "Восьмерка"

В отличие от задачи о миссионерах и каннибалах, эту головоломку можно решить за приемлемое время методом "слепого" поиска. Дело в том, что головоломка имеет только 9! состояний и, следовательно, можно использовать для поиска очередного хода оценочную функцию по методике "восхождения на гору".

I) Придумайте оценочную функцию для этой задачи и разработайте программу, которая реализует поиск по методике "восхождения на гору". Возможные варианты оценочной функции некоторого состояния должны включать, во-первых, количество фишек, которые стоят не на своих местах, а во-вторых, сумму расстояний от текущего положения каждой фишки до предназначенного ей целевого (имеются в виду расстояния по Евклиду).