Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упорядоченные пары действительных чиселСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Билеты Упорядоченные пары действительных чисел Пара чисел является упорядоченной, если указано, какое число из пары является первым и какое - вторым. Комплексными числами называются упорядоченные пары действительных чисел Комплексные числа. Алгебраическая форма комплексного числа. Комплексные числа являются расширением множества действительных чисел. Ко́мпле́ксные чи́сла (устар. мнимые числа) — числа вида
е
Алгебраическая форма Запись комплексного числа Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что
Тригонометрическая форма Если вещественную
Пусть задано комплексное число
Абсциссу
В данном случае
Тогда
Таким образом, для всякого комплексного числа
которое называется тригонометрической формой комплексного числа Определители и их свойства. Матрица – прямоугольная таблица, составленная из элементов произвольной природы. Элементы матрицы располагаются в строки и столбцы (иногда их называют колонками). Строки и столбцы часто называют собирательным термином «ряды матрицы». Элементы матрицы часто обозначают двойными индексами – aij; первый индекс i означает номер строки матрицы, в которой стоит элемент aij, а второй индекс j означает номер столбца матрицы, в котором стоит aij. Матрицы символически обозначают заключёнными в круглые или квадратные скобки, или двойные вертикальные черточки. (Кратко: (aij) или IIaij II). Каждой квадратной матрице, элементами которой являются числа, ставится в соответствие число, называемое определителем матрицы. Опр. Определитель (детерминант) n-го порядка – алгебраическая сумма n! слагаемых членов из элементов квадратной матрицы (таблицы), которое вычисляется по следующему закону: каждое слагаемое есть произведение n элементов взятых по одному и только по одному из каждой строки и из каждого столбца матрицы. Каждый член определителя берётся со знаком (-1)t, где t – число инверсий во вторых индексах члена, когда первые индексы члена расположены в натуральном порядке. Свойства определителя Определитель обладает рядом свойств: 1) Определитель не изменяется при транспортировании матриц (строк и столбцов).2) Если один из столбцов (строк) состоит из нулей, то определитель равен нулю. 3) Если один из определителей получен из другого определителя перестановкой двух столбцов (строк), то определители отличаются друг от друга знаком. 4) Если все элементы какого-либо i-го столбца (строки) определителя являются суммами двух слагаемых, то такой определитель равен сумме двух определителей в первом из которых в качестве i-го столбца (строки) взяты первые слагаемые, а во втором – вторые слагаемые; при этом элементы всех остальных строк (столбцов) у каждого 6. Свойства 8 и 9 определителей. Метод Крамера. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркиванием строки и столбца, на пересечении которых расположен этот элемент. Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное. Алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, кторой обозначен сам элемент. СВОЙСТВО 9. Определитель
равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения. Иначе говоря, имеют место следующие равенства:
го из трёх определителей одинаковы. 5) Определитель, содержащий два пропорциональных, в частности два равных, столбца (строки), равен нулю. 6) Определитель не меняется, если к какому-нибудь столбцу (строке) прибавить линейную комбинацию других столбцов (строк). 7) Если все элементы какого-нибудь столбца (строки) определителя умножить на некоторое число k, то есть весь определитель умножается на k, то общий множитель любой строки или любого столбца можно выносить за знак определителя. Правило Крамера: правило решения системы n линейных уравнений. с n неизвестными, определитель которой отличен от нуля, всегда имеет решение. Это решение единственное и определяется таким правилом Крамера: значение каждого из неизвестных Возведение в степень Возведение матрицы в степень имеет смысл лишь для квадратных матриц (подумайте, почему?). Тогда целой положительной степенью m матрицы A является произведение m матриц, равных A. Так же, как и у чисел. Под нулевой степенью квадратной матрицы A понимается единичная матрица того же порядка что и A. Если позабыли, что такое единичная матрица, гляньте на рис. 3. Транспонирование матриц : Переход от матрицы A к матрице AT, в которой строки и столб цы поменялись местами с сохранением порядка, называется транспонированием матрицы (рис. 8). Обратите внимание, как при транспонировании меняется размер матрицы, то есть количество строк и столбцов. Ранг матрицы Строки и столбцы матрицы являются элементами соответствующих векторных пространств:
Рангом матрицы называют количество линейно независимых столбцов матрицы (столбцовый ранг матрицы) или количество линейно независимых строк матрицы (строчный ранг матрицы). Этому определению эквивалентно определение ранга матрицы как порядка максимального отличного от нуля минора матрицы. При элементарных преобразованиях ранг матрицы не меняется. Свойства линейных операций: Везде далее матрицы 1. Ассоциативность 2. 3. 4. Коммутативность 5. Дистрибутивность 6. 7. Теорема о базисном миноре. В произвольной матрице каждый столбец (строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор. ОПРЕДЕЛЕНИЕ В матрице минор порядка Следствие. Определитель -го порядка равен нулю тогда и только тогда, когда его строки (столбцы) линейно зависимы. Теорема о базисном миноре матрицы служит для доказательства таких важных теорем: Теорема 1. Линейно независимые строки (столбцы) матрицы, количество которых равно рангу матрицы, являются базисными строками (столбцами). Теорема 2. (Теорема о ранге матрицы). Для любой матрицы ее ранг равен максимальному количеству ее линейно независимых строк (столбцов). Критерий совместности СЛАУ Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:
Для того, чтобы линейная система являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы. Необходимость Пусть система совместна. Тогда существуют числа Достаточность Пусть Следствия
Решение СЛАУ общего вида. Основная запись СЛАУ. Понятие решения СЛАУ и некоторые определения.В общем случае основная запись системы n линейных алгебраических уравнений с n неизвестными имеет следующий вид:
При этом через Система называется однородной, если все ее свободные члены Если хотя бы один из свободных членов Решением системы называется такая совокупность Система уравнений вида называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее не существует ни одного решения. Совместная система вида называется определенной, если она имеет единственное решение. Совместная система вида называется неопределенной, если у нее существуют по крайней мере два различных решения.
Краткая запись СЛАУ:
Матричная формулировка СЛАУ:
где
Представление с помощью расширенной матрицы.В действительности, система уравнений полностью определяется элементами матрицы и вектора правой части. Обозначения неизвестных имеют чисто символический смысл. При различных допустимых преобразованиях системы также меняются только значения элементов матрицы и правой части. Поэтому вполне достаточным представлением системы уравнений является, так называемая, расширенная матрица (она получается из матрицы коэффициентов системы путем добавления к этой матрице столбца свободных членов):
где Прямые методами решения СЛАУ называются методы, которые позволяют получить теоретически точное (с учетом ограниченности разрядной сетки ЭВМ) решение за конечное число операций. Прямым методом является, в частности, метод Гаусса, Решение однородной СЛАУ. Любая однородная СЛАУ имеет хотя бы одно решение – нулевое (его ещё называют тривиальное), в котором все переменные равны нулю. Подставим, например, x 1=0, x 2=0, x 3=0 и x 4=0 в записанную выше систему. Получим два верных равенства: {2⋅0−3⋅0−0−0=0;−4⋅0+5⋅0+3⋅0=0. Однако следствие из теоремы Кронекера-Капелли однозначно указывает на то, что если СЛАУ имеет решение, то есть только два варианта. Либо это решение единственно (и тогда СЛАУ называют определённой), либо этих решений бесконечно много (такую СЛАУ именуют неопределённой). С однородными СЛАУ связано дополнительное понятие – фундаментальная система решений. Дело в том, что если ранг матрицы системы однородной СЛАУ равен r, то такая СЛАУ имеет n − r линейно независимых решений: φ 1, φ 2,..., φn − r. Любая совокупность n − r линейно независимых решений однородной СЛАУ называется фундаментальной системой (или совокупностью) решений данной СЛАУ. Часто вместо словосочетания "фундаментальная система решений" используют аббревиатуру "ФСР". Если решения φ 1, φ 2,..., φn − r образуют ФСР, и X – матрица переменных данной СЛАУ, то общее решение СЛАУ можно представить в таком виде: X = C 1⋅ φ 1+ C 2⋅ φ 2+…+ Cn − r ⋅ φn − r, где C 1, C 2,..., Cn − r – произвольные постоянные. Метод Гаусса классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы Поскольку выражение
задает все решения однородной системы, то для любых двух решений
и, следовательно, выражение
определяет любое решение неоднородной системы. Таким образом доказана теорема о структуре общего решения линейной неоднородной системы. Теорема. Если ранг r матрицы неоднородной системы линейных уравнений мерньше числа неизвестных n, то общее решение системы можно записать в виде
где Доказательство Поделим с остатком многочлен
Так как Следствия
Схе́ма Го́рнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы мономов (одночленов), при заданном значении переменной. Метод Горнера позволяет найти корни многочлена[1], а также вычислить производные полинома в заданной точке. Схема Горнера также является простым алгоритмом для деления многочлена на бином вида Разделить 5 x 4+5 x 3+ x 2−11 на x −1, используя схему Горнера. Решение Составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена 5 x 4+5 x 3+ x 2−11, расположенные по убыванию степеней переменной x. Заметьте, что данный многочлен не содержит x в первой степени, т.е. коэффициент перед x в первой степени равен 0. Так как мы делим на x −1, то во второй строке запишем единицу:
Начнем заполнять пустые ячейки во второй строке. Во вторую ячейку второй строки запишем число 5, просто перенеся его из соответствующей ячейки первой строки:
Следующую ячейку заполним по такому принципу: 1⋅5+5=10:
Аналогично заполним и четвертую ячейку второй строки: 1⋅10+1=11:
Для пятой ячейки получим: 1⋅11+0=11:
И, наконец, для последней, шестой ячейки, имеем: 1⋅11+(−11)=0:
Задача решена, осталось только записать ответ:
Как видите, числа, расположенные во второй строке (между единицей и нулём), есть коэффициенты многочлена, полученного после деления 5 x 4+5 x 3+ x 2−11 на x −1. Естественно, что так как степень исходного многочлена 5 x 4+5 x 3+ x 2−11 равнялась четырём, то степень полученного многочлена 5 x 3+10 x 2+11 x +11 на единицу меньше, т.е. равна трём. Последнее число во второй строке (ноль) означает остачу от деления многочлена 5 x 4+5 x 3+ x 2−11 на x −1. В нашем случае остача равна нулю, т.е. многочлены делятся нацело. Этот результат ещё можно охарактеризовать так: значение многочлена 5 x 4+5 x 3+ x 2−11 при x =1 равно нулю. Можно сформулировать вывод и в такой форме: так как значение многочлена 5 x 4+5 x 3+ x 2−11 при x =1 равно нулю, то единица является корнем многочлена 5 x 4+5 x 3+ x 2−11. Основная теорема алгебры. Основна́я теоре́ма а́лгебры утверждает, что поле комплексных чисел алгебраически замкнуто, то есть
Данное утверждение справедливо и для многочленов с вещественными коэффициентами, так как всякое вещественное число является комплексным с нулевой мнимой частью. Не существует строго алгебраического доказательства теоремы — все имеющиеся привлекают неалгебраические концепции, вроде полноты множества вещественных чисел или топологии комплексной плоскости. К тому же, теорема не является "основной" в современной алгебре — она получила это название во времена, когда основным направлением алгебры был поиск решений алгебраических уравнений с вещественными и комплексными коэффициентами. Доказательство Самое простое доказательство этой теоремы даётся методами комплексного анализа. Используется тот факт, что функция, аналитическая на всей комплексной плоскости и не имеющая особенностей на бесконечности, есть константа. Посему, функция 1/p, где p — многочлен, должна иметь хоть один полюс на комплексной плоскости, а, соответственно, многочлен имеет хоть один корень. Следствие Немедленным следствием из теоремы является то, что любой многочлен степени Доказательство следствия У многочлена Формулы Виета. Формулы Виета — формулы, выражающие коэффициенты многочлена через его корни. Этими формулами удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным корням. Если
(каждый корень взят соответствующее его кратности число раз), то коэффициенты
Иначе говоря Если старший коэффициент многочлена Доказательство Доказательство осуществляется рассмотрением равенства, полученного разложением многочлена по корням, учитывая, что
Приравнивая коэффициенты при одинаковых степенях P.S. Пожалуйста, не ленитесь, проверяйте ответ, приводя к общему знаменателю полученное разложение. Метод неопределенных коэффициентов является универсальным способом при разложении дроби на простейшие. Очень удобно использовать метод частных значений, если знаменатель представляет собой произведение линейных множителей, то есть имеет вид схожий с Рассмотрим на примере, чтобы показать плюсы этого метода. Умножение вектора на число Определение Произведением 1. 2. 3. Свойства умножения вектора на число: 1. 2. 3. 4. 5. 6. Здесь Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность равную 3. В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов: конечномерное вещественное векторное пространство
Для определения евклидова пространства проще всего взять в качестве основного понятие скалярного произведения. Евклидово векторное пространство определяется как конечномерное векторное пространство над полем вещественных чисел, на векторах которого задана вещественнозначная функция
Аффинное пространство, соответствующее такому векторному пространству, называется евклидовым аффинным пространством, или просто евклидовым пространством[1]. Пример евклидова пространства — координатное пространство Базис и координаты вектора Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов. В случае, когда базис бесконечен, понятие «линейная комбинация» требует уточнения. Это ведёт к двум основным разновидностям определения:
В конечномерных пространствах обе разновидности базиса совпадают. Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
где Скалярное произведение. операция над двумя векторами, результатом которой является число [когда рассматриваются векторы, числа часто называют скалярами], не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю. Скалярное произведение двух вект
|
||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 1332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 , где
, где  и
и  — вещественные числа,
— вещественные числа,  — мнимая единица (величина, для которой выполняется равенство:
— мнимая единица (величина, для которой выполняется равенство:  ). Действия над комплексными числами
). Действия над комплексными числами означает, что
означает, что  и
и  (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
(два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).



 Если комплексное число
Если комплексное число  , то число
, то число  называется сопряжённым (или комплексно сопряжённым) к
называется сопряжённым (или комплексно сопряжённым) к  (часто обозначается также
(часто обозначается также  ). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.
). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком. , называется алгебраической формой комплексного числа.
, называется алгебраической формой комплексного числа.

 и аргумент
и аргумент  (
( ,
, 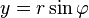 ), то всякое комплексное число
), то всякое комплексное число 
 . Как известно, его можно изобразить на комплексной плоскости точкой, абсцисса которой равна действительной части этого числа, то есть
. Как известно, его можно изобразить на комплексной плоскости точкой, абсцисса которой равна действительной части этого числа, то есть  , а ордината - мнимой части
, а ордината - мнимой части  (рис. 1).
(рис. 1).
 и аргумент
и аргумент 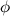 следующим образом:
следующим образом:
 удовлетворяют соотношениям:
удовлетворяют соотношениям:



 .
.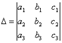
 ,
, 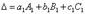 ,
, ,
,  ,
, ,
,  .
. , где
, где  - определитель системы., матрица которого составлена из коэффициентов при неизвестных системы, а
- определитель системы., матрица которого составлена из коэффициентов при неизвестных системы, а  I – определитель, матрица которого получена заменой столбца коэффициентов при данном неизвестном на столбец свободных членов системы. В случае если определитель системы равен нулю, система имеет бесконечно много решений.
I – определитель, матрица которого получена заменой столбца коэффициентов при данном неизвестном на столбец свободных членов системы. В случае если определитель системы равен нулю, система имеет бесконечно много решений. составляют элементы пространства размерности
составляют элементы пространства размерности  ;
;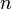 .
. ,
,  и
и  - матрицы одного размера.
- матрицы одного размера.
 , где
, где  - нулевая матрица соответствующего размера.
- нулевая матрица соответствующего размера.




 называется базисным, если он не равен нулю, а все миноры порядка и выше равны нулю или не существуют вовсе, т.е. совпадает с меньшим из чисел или.
называется базисным, если он не равен нулю, а все миноры порядка и выше равны нулю или не существуют вовсе, т.е. совпадает с меньшим из чисел или. такие, что
такие, что  . Следовательно, столбец
. Следовательно, столбец  является линейной комбинацией столбцов
является линейной комбинацией столбцов  матрицы
матрицы  .
.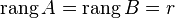 . Возьмем в матрице
. Возьмем в матрице  , то он же и будет базисным минором и матрицы
, то он же и будет базисным минором и матрицы  . Тогда, согласно теореме о базисном миноре, последний столбец матрицы
. Тогда, согласно теореме о базисном миноре, последний столбец матрицы  (2.2.1)
(2.2.1) обозначены неизвестные, подлежащие определению; величины
обозначены неизвестные, подлежащие определению; величины  называемые коэффициентами системы, и величины
называемые коэффициентами системы, и величины  , называемые свободными членами, предполагаются известными. Каждый коэффициент системы
, называемые свободными членами, предполагаются известными. Каждый коэффициент системы  имеет два индекса, первый из которых
имеет два индекса, первый из которых  указывает номер уравнения, а второй
указывает номер уравнения, а второй  номер неизвестного, при котором стоит этот коэффициент.
номер неизвестного, при котором стоит этот коэффициент. равны нулю.
равны нулю. отличен от нуля, то система называется неоднородной.
отличен от нуля, то система называется неоднородной. чисел
чисел 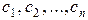 , которая при подстановке в систему на место неизвестных
, которая при подстановке в систему на место неизвестных  . (2.2.2)
. (2.2.2) , (2.2.3)
, (2.2.3) ; (2.2.4)
; (2.2.4) – матрица коэффициентов системы;
– матрица коэффициентов системы;  – вектор неизвестных;
– вектор неизвестных;  – вектор свободных членов.
– вектор свободных членов. (2.2.5)
(2.2.5) .
.
 и
и 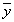 неоднородной системы справедливо
неоднородной системы справедливо


 — произвольные константы, а
— произвольные константы, а  — фундаментальная система решений однородной системы,
— фундаментальная система решений однородной системы,  на многочлен
на многочлен  :
:
 , то
, то  — многочлен степени не выше 0. Подставляя
— многочлен степени не выше 0. Подставляя  , поскольку
, поскольку 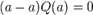 , имеем
, имеем  .
.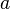 является корнем многочлена
является корнем многочлена  тогда и только тогда, когда
тогда и только тогда, когда  тождественно множеству корней соответствующего уравнения
тождественно множеству корней соответствующего уравнения 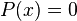 ).
). с целыми коэффициентами. Тогда для любого целого
с целыми коэффициентами. Тогда для любого целого  число
число  делится на
делится на  .
.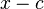 . Метод назван в честь Уильяма Джорджа Горнера. Пример №1
. Метод назван в честь Уильяма Джорджа Горнера. Пример №1
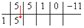





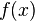 есть корень
есть корень 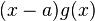 , где
, где 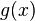 — другой многочлен. Применим теорему к
— другой многочлен. Применим теорему к  — корни многочлена
— корни многочлена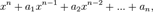

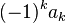 равно сумме всех возможных произведений из
равно сумме всех возможных произведений из  , то для применения формулы Виета необходимо предварительно разделить все коэффициенты на
, то для применения формулы Виета необходимо предварительно разделить все коэффициенты на 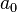 (это не влияет на значение корней многочлена). В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленен.
(это не влияет на значение корней многочлена). В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленен.
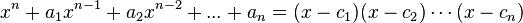


 вектора
вектора 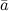 на число
на число  называется вектор
называется вектор  , удовлетворяющий условиям:
, удовлетворяющий условиям:
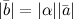
 , если
, если  ,
,  , если
, если  .
.


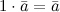
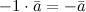
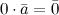
 - произвольные числа.
- произвольные числа. с введённым на нём положительно определённым скалярным произведением, либо метрическое пространство, соответствующее такому векторному пространству. В этой статье за исходное будет взято первое определение.
с введённым на нём положительно определённым скалярным произведением, либо метрическое пространство, соответствующее такому векторному пространству. В этой статье за исходное будет взято первое определение. также часто используется обозначение
также часто используется обозначение  обладающая следующими тремя свойствами:
обладающая следующими тремя свойствами: и для любых вещественных чисел
и для любых вещественных чисел  и
и 

 причём
причём 
 состоящее из всевозможных n -ок вещественных чисел
состоящее из всевозможных n -ок вещественных чисел  скалярное произведение в котором определяется формулой
скалярное произведение в котором определяется формулой 


 — координаты вектора.
— координаты вектора.