
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение матрицы линейного оператора к диагональному виду⇐ ПредыдущаяСтр 12 из 12
Матрица линейногопреобразования имеет диагональный вид
Тогда и только тогда, когда каждый базисный вектор является собственным вектором этого преобразования. Матрица.
Где Т е ор е м а 10.7. Матрица Если все собственные числа матрицы Действия над линейными операторами Во множестве всех операторов, действующих из L1 в L2 можно определить операции суммы таких операторов и умножения на скаляр: А) суммой двух операторов Б) произведением оператора В) нулевым оператором 0 назовем оператор, который действует по правилу 0×х = 0 для любого Х; Г) для каждого оператора 55. Невырожденные линейные преобразования Линейное преобразование называется невырожденным, если его матрица является невырожденной; в противном случае линейное преобразование называется вырожденным. Теорема 10.10. Линейное преобразование является невырожденным тогда и только тогда, когда оно взаимно однозначно. Следствие. Линейное невырожденное преобразование ненулевой вектор переводит в ненулевой; обратно также верно: если линейное преобразование ненулевой вектор переводит в ненулевой, то оно будет невырожденным. Ортогональные матрицы Ортогональная матрица — квадратная матрица A с вещественными элементами, результат умножения которой на AT равен единичной матрице:[1]
или, что эквивалентно, её обратная матрица равна транспонированной матрице:
57. Ортогональные преобразования Ортогональное преобразование — линейное преобразование
где треугольными скобками обозначено скалярное произведение Свойства
где
58. Квадратичные формы. Преобразование квадратичной формы при линейном преобразовании переменных. Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора. Линейное преобразование (1) переменных называется неособенным, если его матрица С неособенная (det C. Если линейное преобразование с матрицей С неособенное, то существует обратная матрица С-1 и преобразование У=С-1∙Х называется обратным преобразованием переменных. Определение 3. Собственные значения и собственные векторы матрицы линейного преобразования называются собственными значениями и собственными векторами линейного преобразования.
Если в квадратичной форме с матрицей А сделано неособенное линейное преобразование переменных Х = С∙ У, то новая квадратичная форма имеет матрицу В = СТ∙А∙С.
|
||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 694; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.106.100 (0.005 с.) |

 Называется приводимой к диагональному виду, если существует невырожденная матрица
Называется приводимой к диагональному виду, если существует невырожденная матрица  Такая, что матрица
Такая, что матрица  Является диагональной. Следовательно, если матрица
Является диагональной. Следовательно, если матрица 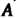 Приводима к диагональному виду, то
Приводима к диагональному виду, то
 - характеристические числа матрицы
- характеристические числа матрицы 
 Линейногопреобразования
Линейногопреобразования  -мерного линейного пространства приводима к диагональному виду тогда и только тогда, когда существует базис этого пространства, состоящий из собственных векторов данного преобразования.
-мерного линейного пространства приводима к диагональному виду тогда и только тогда, когда существует базис этого пространства, состоящий из собственных векторов данного преобразования. Попарно различны, то матрица приводится к диагональному виду.
Попарно различны, то матрица приводится к диагональному виду. и
и  назовем оператор (
назовем оператор (

 евклидова пространства
евклидова пространства  , сохраняющее длины или (что эквивалентно) скалярное произведение векторов. Это означает, что для любых двух векторов
, сохраняющее длины или (что эквивалентно) скалярное произведение векторов. Это означает, что для любых двух векторов 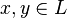 выполняется равенство
выполняется равенство
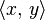 в пространстве
в пространстве 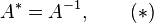
 — сопряжённое, а
— сопряжённое, а  — обратное преобразования.
— обратное преобразования. или
или  , а собственные векторы (вообще говоря, комплексные), отвечающие различным собственным значениям, ортогональны.
, а собственные векторы (вообще говоря, комплексные), отвечающие различным собственным значениям, ортогональны.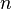 -мерном евклидовом пространстве ортогональное преобразование является композицией конечного числа отражений.
-мерном евклидовом пространстве ортогональное преобразование является композицией конечного числа отражений.


