
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действительные числа в курсе математики 8 классаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Изучение действительных чисел в курсе алгебры 8 класса связано с введением квадратного корня из числа, который, как известно, может быть числом иррациональным. Содержание учебного материала. 1. Рациональные числа. 2. Иррациональные числа.
1. Изучение действительных чисел начинается с повторения чисел рациональных (от латинского ratio – отношение). В объяснительном тексте учебника повторяются натуральные, целые и рациональные числа. Вводятся обозначения: N – множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел. Используются знаки Î и Ï для записи утверждения, что число является или не является элементом данного числового множества. Основное внимание уделяется числам рациональным, которые состоят из чисел целых и дробных. Далее рассматриваются представления рациональных чисел в виде дроби. Всякое рациональное число (как целое, так и дробное) можно представить в виде обыкновенной дроби Замечание. Существуют правила представления бесконечной десятичной периодической дроби в виде рационального числа. Однако в школе они не рассматриваются. Приведём хитроумный способ такого представления. Например, дробь 0, (17). Пусть 0, (17)=х. Тогда 100х=17,(17). Вычтем из второго равенства первое. 99х=17, х=17/99. 2. Иррациональные числа вводятся посредством операции измерения отрезка. Пусть точка О – начальная точка координатной прямой и отрезок ОЕ – единица измерения. Чтобы измерить отрезок ОВ с помощью единицы измерения ОЕ, поступают следующим образом
Рис. 5 Откладывают от точки О единицу измерения – отрезок ОЕ. Он уложился в отрезке ОВ 2 раза. Значит длина отрезка ОВ» 2. Чтобы получить более точный результат, разделим отрезок ОЕ на 10 равных частей. Десятая часть отрезка ОЕ укладывается в остатке СВ 3 раза. Приближённое значение длины отрезка АВ с точностью до 0,1 равно 2,1. Продолжая процесс измерения, мы будем использовать 0,01; 0,001... доли единичного отрезка, получая приближённые значения длины отрезка АВ с точностью до 0,01; 0,001... В процессе десятичного измерения могут представиться два случая: 1) на каком – то шаге не получится остатка;
2) остатки будут получаться на каждом шаге. В первом случае результатом измерения окажется натуральное число или конечная десятичная дробь, во втором случае бесконечная десятичная дробь. Так как всякое натуральное число и конечную десятичную дробь можно представить в виде бесконечной десятичной дроби, то можно считать, что результатом десятичного измерения длины отрезка всегда является бесконечная десятичная дробь. Далее на примерах убеждаемся, что длина отрезка может выражаться бесконечной десятичной периодической дробью либо бесконечной десятичной непериодической дробью. Пример 1. Пусть ОС=7/4 единичного отрезка. При десятичном измерении его длины получим число 1,75. Пример 2.Пусть отрезок ОF = 8/3 единичного отрезка. длины При десятичном измерении его длины получится число 2,666... Пример 3. Пусть стороной квадрата служит отрезок длиной 1. Измерим с помощью этой единицы диагональ квадрата ОК.
Рис. 6
Длина отрезка ОК – сторона квадрата, площадь которого в 2 раза больше площади данного квадрата, равной 1. Следовательно, площадь большого квадрата равна 2. Следовательно, квадрат длины отрезка ОК равен 2. Докажем, что рационального числа, квадрат которого равен 2 не существует. Метод: от противного. Пусть такое рациональное число существует, то есть (
В учебнике содержится ещё один важный вывод: десятичное измерение длин отрезков каждой точке координатной прямой, лежащей справа от начальной точки О, ставит в соответствие положительную бесконечную десятичную дробь. Наоборот, взяв произвольную положительную бесконечную десятичную дробь, мы можем найти на координатной прямой справа от точки О единственную точку А, такую, что длина отрезка Оа выражается этой дробью. Замечание. Рассмотренный материал достаточно трудно усваивается 8-классниками, но, к сожалению, в дальнейшем к изучению числовых систем учащиеся общеобразовательных классов не возвращаются. Литература. 1. Математика: Учебник для 5 кл, общеобразоват. учреждений /Н.Я. Виленкин, В.И. Жохов и др. 2. Математика: Учебник для 6 кл, общеобразоват. учреждений /Н.Я. Виленкин, В.И. Жохов и др. 3. Алгебра: Учебник для 8 кл. сред. шк./ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др; Под ред. С. А. Теляковского. - М.: Просвещение, 2003 г. 2. Сборник нормативных документов. Математика / сост. Э.Д. Днепров, А.Г. Аркадьев. 3. Жохов В.И. и др. Примерное планирование учебного материала и контрольные работы по математике, 5 – 9 классы. 4.Методика и технология обучения математике. Курс лекций: пособие для вузов/под научн. ред.Н.Л. Стефановой. – М.: Дрофа, 2005 г. 5. Методика преподавания математики в средней школе. Частные методики/ Ю.М. Колягин и др. - М., Просвещение, 1977
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 766; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.62.168 (0.01 с.) |

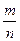 , где т – целое число, а п – натуральное число. На ряде примеров (без доказательства) делением числителя на знаменатель учащиеся убеждаются, что каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби. При этом конечные десятичные дроби рассматриваются как бесконечные периодические с периодом 0. Верно и обратное утверждение: каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число.
, где т – целое число, а п – натуральное число. На ряде примеров (без доказательства) делением числителя на знаменатель учащиеся убеждаются, что каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби. При этом конечные десятичные дроби рассматриваются как бесконечные периодические с периодом 0. Верно и обратное утверждение: каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число.


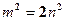 , т 2 – число чётное, значит и т – число чётное. Пусть
, т 2 – число чётное, значит и т – число чётное. Пусть 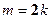 , тогда
, тогда 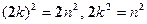 , то есть п 2, а значит и п – число чётное. Тогда дробь
, то есть п 2, а значит и п – число чётное. Тогда дробь 


