
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обыкновенные дроби в курсе математики 6 классаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Частично материал изучен в 5 классе. Главное – сформировано понятие дробного числа. Содержание учебного материала в курсе 6 класса 1. Основное свойство дроби. 2. Сокращение дробей. 3. Приведение дробей к общему знаменателю. 4. Сравнение, сложение и вычитание дробей с разными знаменателями. 5. Сложение и вычитание смешанных чисел. 6. Умножение дробей. 7. Нахождение дроби от числа. 8. Применение распределительного свойства умножения. 9. Взаимно обратные числа. 10. Деление. 11.Нахождение числа по его дроби. 12. Дробные выражения. 4. Наиболее трудными для усвоения являются действия сложения и вычитания дробей с разными знаменателям, основанные на операции приведения дробей к наименьшему общему знаменателю. Учащимся предлагается алгоритм: чтобы привести дроби к наименьшему общему знаменателю надо: 1) найти наименьшее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем; 2) разделить наименьший общий знаменатель на знаменатели данных дробей, то есть найти дополнительные множители; 3) умножить числитель и знаменатель каждой дроби на её дополнительный множитель. При этом первый пункт также предполагает достаточно сложный алгоритм: чтобы найти наименьшее общее кратное нескольких чисел надо: 1) разложить их на простые множители; 2) выписать множители, входящие в разложение одного из чисел; 3) добавить к ним недостающие множители из разложения остальных чисел; 4) найти произведение получившихся множителей. Пример. Привести дроби Решение. 1) 60= 2×2×3×5; 168= 2×2×2×3×7. Наименьший общий знаменатель: 2×2×2×3×5×7=840. 2) 840:60=14, 840:168=5 – дополнительные множители. 3) Далее, научить сравнивать, складывать и вычитать дроби с разными знаменателями не представляется затруднительным, так как эти операции основаны на приведении дробей к наименьшему общему знаменателю. 5. Другое трудно усваиваемое действие – вычитание смешанных чисел. Для обоснования алгоритма этого действия используются свойства вычитания суммы из числа и числа из суммы: (а + в)- с =(а - с)+ в=а+ (в-с); а -(в + с)= а - в - с. Например,
Например, Далее учащимся предлагается сложный алгоритм вычитания смешанных чисел. 6. Действие умножения обыкновенных дробей разделено на 2 этапа. Первоначально рассматривается умножение дроби на натуральное число. Предлагается задача: в бутылке 3/4 литра сока. Сколько сока в 5 таких бутылках? Решение: 3/4×5=3/4+3/4+3/4+3/4+3/4=15/4=3 Иначе тот же результат можно получить так: Вводится правило умножения дроби на натуральное число. Далее учащимся предлагается задача: длина прямоугольника равна 4/5 дм, а ширина 2/3 дм. Чему равна площадь прямоугольника? (Её решение рассмотрено в общей методике при обсуждении места задач в процессе изучения нового материала). Введённое правило умножения дробей не вызывает затруднений у учащихся. 10. Для введения правила деления дробных чисел используется понятие взаимно обратных чисел. Два числа, произведение которых равно 1 называются взаимно обратными. Учащимся предлагается задача: площадь прямоугольника 5/7 м2. Длина одной его стороны 3/4 м. Найти длину другой стороны. Решение задачи сводится к решению уравнения 3/4 х =5/7, где х – искомая сторона прямоугольника. Умножая обе части уравнения на число 4/3, получим х =5/7×4/3, с другой стороны х =5/7:3/4. Следовательно, 5/7:3/4=5/7×4/3. Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю. 8. Важную роль для формирования вычислительной культуры учащихся играет пункт «Применение распределительного свойства умножения». Так, используя распределительный закон умножения относительно сложения и вычитания, учащиеся получаю возможность рационализации вычислений. Например, 12. В пункте учебника «Дробные выражения» предполагается изучение совместных действий над десятичными и обыкновенными дробями. Частное двух чисел или выражений, в котором знак деления обозначается дробной чертой, называется дробным выражением. Например, Чтобы найти значение такого выражения, учащиеся должны определить, в каких дробях выполнять действия. По всей видимости, было бы полезно сообщить им, какая обыкновенная дробь может быть представлена конечной десятичной дробью (в разложении знаменателя которой на простые множители не содержится других чисел, кроме 2 и 5). В учебнике такие сведения отсутствуют.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 856; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.75.217 (0.006 с.) |

 к наименьшему общему знаменателю.
к наименьшему общему знаменателю.
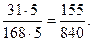
 Другая сложность возникает в случае, когда дробная часть уменьшаемого меньше дробной части вычитаемого. Учащимся сообщается дополнительное правило: если дробная часть уменьшаемого окажется меньше дробной части вычитаемого, то надо превратить в дробь с тем же знаменателем одну единицу целой части уменьшаемого.
Другая сложность возникает в случае, когда дробная часть уменьшаемого меньше дробной части вычитаемого. Учащимся сообщается дополнительное правило: если дробная часть уменьшаемого окажется меньше дробной части вычитаемого, то надо превратить в дробь с тем же знаменателем одну единицу целой части уменьшаемого.







