
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Евклидово пространство. Неравенство Коши-Буняковского треугольника.
Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность равную 3. В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов: конечномерное вещественное векторное пространство
Неравенство Коши — Буняковского — Шварца и неравенство треугольника В данном выше определении угла остался один пробел: для того, чтобы Ортонормированная система векторов евклидового пространства Ортонормированные базисы Ортонормированный базис в евклидовом (векторном) пространстве — это базис, состоящий из попарно ортогональных векторов единичной нормы. Ортонормированные базисы наиболее удобны для вычислений. Так, например, скалярное произведение векторов с координатами
49. Линейный оператор и его матрица. Линейное преобразование в координатах. Рассмотрим линейный оператор A, действующий в конечномерном линейном пространстве X, dim(x)=n и пусть e1, e2,..., en - базис в X. Обозначим через A e1 = (a11,...,an1),..., A en = (a1n,...,ann) образы базисных векторов e1, e2,..., en. Матрица
Столбцами которой являются координаты образов базисных векторов, называется матрицей линейного оператора в заданном базисе. Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, отвечает единственная квадратная матрица порядка n; и обратно
с одной стороны, связывают координаты образа y = A x с координатами прообраза X, с другой стороны, описывают действие оператора, заданного матрицей A.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 364; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.198.43 (0.007 с.) |
 с введённым на нём положительно определённым скалярным произведением, либо метрическое пространство, соответствующее такому векторному пространству. В этой статье за исходное будет взято первое определение.
с введённым на нём положительно определённым скалярным произведением, либо метрическое пространство, соответствующее такому векторному пространству. В этой статье за исходное будет взято первое определение.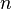 -мерное евклидово пространство обозначается
-мерное евклидово пространство обозначается  также часто используется обозначение
также часто используется обозначение 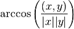 был определён, необходимо, чтобы выполнялось неравенство
был определён, необходимо, чтобы выполнялось неравенство 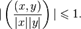 Это неравенство действительно выполняются в произвольном евклидовом пространстве, оно называется неравенством Коши — Буняковского — Шварца. Из этого неравенства, в свою очередь, следует неравенство треугольника:
Это неравенство действительно выполняются в произвольном евклидовом пространстве, оно называется неравенством Коши — Буняковского — Шварца. Из этого неравенства, в свою очередь, следует неравенство треугольника: 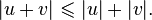 Неравенство треугольника, вместе с перечисенными выше свойствами длины, означает, что длина вектора является нормой на евклидовом векторном пространстве, а функция
Неравенство треугольника, вместе с перечисенными выше свойствами длины, означает, что длина вектора является нормой на евклидовом векторном пространстве, а функция 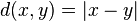 задаёт на евклидовом пространстве структуру метрического пространства (эта функция называется евклидовой метрикой). В частности, расстояние между элементами (точками)
задаёт на евклидовом пространстве структуру метрического пространства (эта функция называется евклидовой метрикой). В частности, расстояние между элементами (точками)  и
и  координатного пространства
координатного пространства 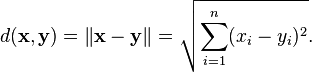
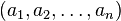 и
и 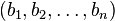 в ортонормированном базисе можно вычислять по формуле
в ортонормированном базисе можно вычислять по формуле 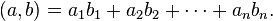 В любом евклидовом пространстве существует ортонормированный базис. Выбрав в двух евклидовых пространствах ортонормированные базисы и переведя один из них в другой линейным отображением, можно доказать, что любые два евклидовых пространства одинаковой размерности изоморфны (в частности,
В любом евклидовом пространстве существует ортонормированный базис. Выбрав в двух евклидовых пространствах ортонормированные базисы и переведя один из них в другой линейным отображением, можно доказать, что любые два евклидовых пространства одинаковой размерности изоморфны (в частности, 
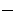 каждая квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения
каждая квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения






