
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет многопролетной статически определимой шарнирной балки на действие постоянной нагрузкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для балки, выбранной согласно варианту (рис.3.) и исходных данных (табл. 1), необходимо: 1 Выполнить кинематический анализ расчетной схемы балки. 2 Построить поэтажную схему балки. 3 Построить эпюры поперечных сил Qy и изгибающих моментов Mz.
Таблица 1. Исходные данные для балки.
Рисунок 3 Расчетно -графическое задание №2 Расчет многопролетной статически определимой шарнирной балки на действие постоянной нагрузки Для одной из балок (рис.4) с исходными данными (табл. 2), которые отвечают шифру зачетной книжки студента, необходимо: 1 Выполнить кинематический анализ расчетной схемы балки. 2 Построить поэтажную схему балки. 3 Построить эпюры поперечных сил Qy и изгибаемых моментов Mz.
Таблица 2. Исходные данные для балки
Пример 2 Для заданной схемы балки (рис. 5): 1 Выполнить кинематический анализ расчетной схемы балки. 2 Построить поэтажную схему балки. 3 Построить эпюры Qy и Mz.
Рисунок 5 1 Выполняем кинематический анализ расчетной схемы балки (рис. 5). П = 3 Д – 2 ш - Coп = 3∙2-2∙1-4 = 0, то есть необходимое условие геометрической неизменяемости выполняется. 2 Строим поэтажную схему балки (рис. 5,а). 3 Строим эпюры внутренних усилий Qy и Mz. А) Расчет начинаем с верхней балки 3-4 (рис. 6).
∑М4 = 0 -R3 ∙11+20∙11∙5∙5-80∙2 = 0 R3 = 95,5кН 0 ≤х1≤11м
Qy = 95,5-20∙х1 = 0 х1 = 4,8м
˟
Б) Дальше рассматриваем элемент 1-2-3. В точке 3 добавляем силу R3 = 95,5кН и направляем ее вниз (это давление верхней балки на нижнюю в точке 3 (рис.7)). ∑Mz = 0; R1∙9-20-95,5∙1-20∙1∙0,5=0; R1 = 13,9кН.
Qy = 0, Mz = +20 кН∙м.
0 ≤ х4≤ 9м Qy = -13,9 кН, Mz = +20-13,9∙ х4, х4 = 0, Mz = + 20 кН∙м, х4 = 9м, Mz = -105,5 кН∙м.
0 ≤ х5≤ 1м Qy =+95,5 +20∙ х5, x5= 0, Qy = +95,5кН, x5= 1м, Qy = +115,5 кН.
По полученным значениям Qy и Mz (рис. 6, 7) строим результирующие эпюры на общей оси для всей балки (рис 5,б; 5,в).
Тема 2. Расчет плоской статически определимой фермы Общие указания Ферма - это стержневая система, которая после введения шарниров во все жесткие узлы будет геометрически неизменяемой системой. В расчетных схемах плоских ферм обычно предусматривается наличие идеальных шарниров, лишенных трения. Сами стержни предусматриваются строго прямолинейными. Оси всех стержней пересекаются в центре узла. Предусматривается также, что нагрузка расположена в узлах. При этих условиях стержни ферм работают на растяжение или сжатие. В шарнирных соединениях элементов моменты в стержнях равняются нулю. Расчет плоских ферм заключается в определении продольных усилий в ее стержнях методом сквозных сечений или методом вырезания узлов. Так как величины внутренних усилий неизвестны не только по величине, но и по направлению, то первоначально их направляют положительно (растянутыми), то есть от узла или от сечения. Если полученное продольное усилие имеет знак «плюс», то стержень растянут, если «минус» - сжат. Для нахождения внутренних усилий методом сквозных сечений разделяют ферму сечением на две части и рассматривают равновесие одной из частей. Этот способ расчета позволяет определить усилие в каждом из стержней при помощи одного уравнения: å Fx = 0, å Fу = 0 или å М = 0 (это точка пересечения осей двух стержней в данном сечении).
При определении усилий методом вырезания узлов усилия определяют при помощи уравнения å Fx = 0 или å Fу = 0, при этом определять усилия надо начинать с узла, в котором сходиться не более двух стержней.
Пример 3 Определить усилия в стержнях второй панели фермы, изображенной на рисунке 8. Для определения усилий используем метод сквозных сечений и вырезания узлов.
1 Определяем опорные реакции.
H1 – 10 = 0 H1 = 10 кН.
2 Определяем усилия. Для этого проводим сечение m-m. Рассматриваем левую часть (рис.8,б). Неизвестные усилия направляем в положительном направлении (то есть от узла).
N9-8 ∙ 2 + 12,5 ∙4 = 0 N9-8 = -25 кН. Знак «минус» указывает на то, что усилие N9-8 не растягивающее, а сжимающее.
Знак «плюс» указывает на то, что стержень
Для определения усилий в стержне
Расчетно-графическое задание №3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 1109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.182.74 (0.008 с.) |


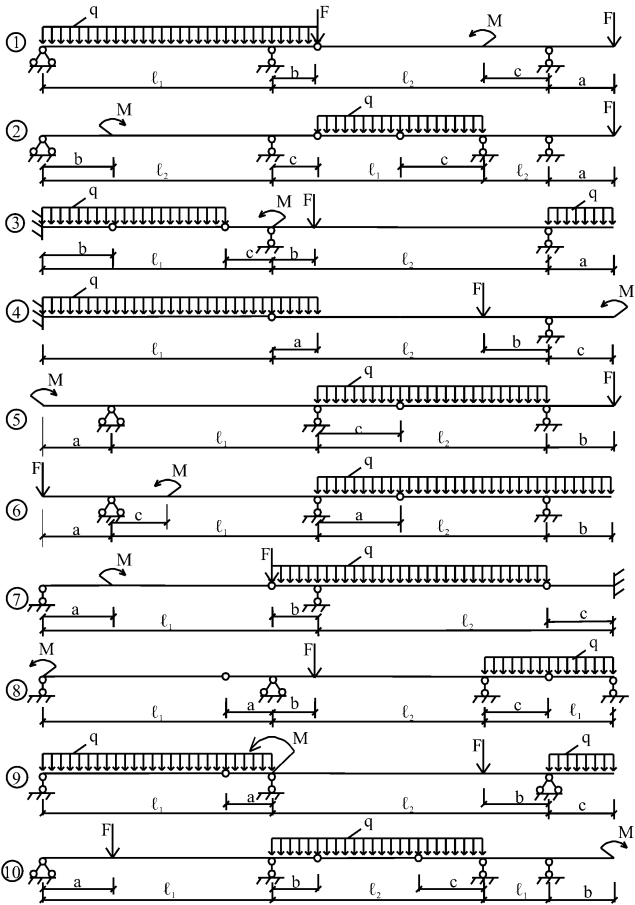 Рисунок 4
Рисунок 4


 = 95,5 ∙ 4,8 – 20 ˟
= 95,5 ∙ 4,8 – 20 ˟ = +228 кН∙м.
= +228 кН∙м. 0 ≤ х3≤ 2м
0 ≤ х3≤ 2м
 ,
, ,
,  кН.
кН. ,
, ,
,  кН.
кН.
 ,
, ,
, ,
,  ,
,  кН.
кН.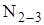 растянут.
растянут. ,
,  ,
,  кН.
кН. вырезаем узел 9 (рис.8,в).
вырезаем узел 9 (рис.8,в). ,
,  кН.
кН.


