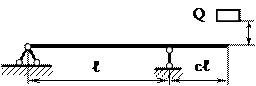Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет балки, изображенной на рисунке 12. 1а.Содержание книги
Поиск на нашем сайте
Прогиб Δст середины балки (в сечении под грузом Р) от статического действия силы Р = 4000 Н. Δст = Не учитывая влияния собственного веса системы, подвергающейся удару, находим динамический коэффициент: kд = 1 + Наибольший изгибающий момент Мот статически действующей силы Р равен Р·ℓ/4; он возникает в поперечном сечении балки под этой силой.
Наибольшие нормальные напряжения от статически действующей силы Р равны σст = Определяем динамические напряжения при ударе без учета собственного веса балки: σ = kд·σст = 24,8·8,45 = 209,5 МПа(2095 кгс/см2). При расчете с учетом собственного веса балки динамический коэффициент определяем по формуле: kд = 1 + = 1+ Здссь Q= q·ℓ = 279·2 = 558 Н (55,8 кгс) — вес балки; β — коэффициент приведения распределённой массы балки к сосредоточенной. Для случая изгибающего удара по середине балки, лежащей на двух жестких опорах, равный 17/35 (таблица 12.1). Динамические напряжения при учете собственного веса балки σ = kд·σст = 24,1·8,45 = 203,5 МПа(2035 кгс/см2). Для определения полных напряжений к ним надо добавить напряжения от собственного веса балки, равные
σп = 203,5 + 0,6 = 204,1 МПа (2041 кгс/см2). В данном случае в связи с незначительным весом балки по сравнению с весом падающего груза влияние собственного веса на результаты расчета несущественно. 12.2. Расчет балки, изображенной на рис. 12.16. В случае опирания левого конца балки на пружину при действии на балку статической силы Рпружина под влиянием опорной реакции, равной Р/2,укоротится на величину а = Р/(2С),где С —жесткость пружины, равная С=500·103Н/м (500кгс/см). Левый конец балки при этом опустится на величину а(рисунок 12.1в), асередина балки — на величину
Полное вертикальное перемещение от статического действия силы Рв сечении под силой (по середине балки) равно сумме величин прогиба, найденного при расчете балки без пружины, и перемещения, вызванного сжатием пружины, т. е. Δст = 0,0141+0,2 = 0,2141 см. Находим динамический коэффициент (без учета собственного веса балки): kд = 1 + Наибольшее нормальное напряжение от статической силы в данном случае такое же, как и напряжение, подсчитанное для балки, не опертой на пружину, т. е. σст = 8,45 МПа (84,5 кгс/см2).
По формуле (14.14) находим σ = kд·σст = 7,19·8,45 = 60,8 МПа(608 кгс/см2). Таким образом, установка пружины под один конец балки уменьшила динамические напряжения примерно в 3,5 раза (209,5/60,8).
Таблица 12.1
ЛИТЕРАТУРА 1. Дарков А. В., Шпиро Г. С. Сопротивление материалов, М., 1965 и 1975 гг. 2. Смирнов А. Ф. и др. Сопротивление материалов, 1975. 3. Феодосьев В. И. Сопротивление материалов, М., 1974. 4. Беляев Н. М. Сопротивление материалов, М., 1976. 5. Сборник задач по сопротивлению материалов под редакцией В. К. Качурина, М., 1972. 6. Уманский А. А. Сборник задач по сопротивлению материалов, М., 1973 7Миролюбов И. Н. и др. Пособие к решению задач по сопротивлению материалов, М., 1962. 8. Писаренко Г. С. и др. Справочник по сопротивлению материалов, Киев, 1975. 9. Любошиц М. И., Ицкович Г. М. Справочник по сопротивлению материалов, Минск, 1969. СОДЕРЖАНИЕ
8. К ЗАДАЧЕ № 8 ВНЕЦЕНТРЕННОЕ СЖАТИЕ...................... 3 8,1. Определение положения центра тяжести сечения...................... 4 8.2. Вычисление главных центральных моментов и радиусов инерции 6 8.3. Определение положения нейтральной оси................................... 6 8.4. Определение опасных точек, запись условий прочности и определение допускаемой нагрузки............................................................................................................ 7 8.5. Построение эпюры напряжений.................................................... 7 9... К ЗАДАЧЕ № 9. ИЗГИБ С КРУЧЕНИЕМ ЛОМАНОГО СТЕРЖНЯ 9 9.1. Пример «а»................................................................................... 9 9.1.1. Построение эпюры крутящих моментов. 9 9.1.2. Построение эпюры изгибающих моментов сил...................... 10 9.2. Пример «б»................................................................................. 12 10............................. К ЗАДАЧЕ №10. РАСЧЕТ КРИВОГО БРУСА 14 10.1. Определение опорных реакций................................................. 15 10.2. Построение эпюр M, N и Q........................................................ 16 10.3. Определение напряжений.......................................................... 20 10.3.1. Круглое сечение......................................................................... 21 10.3.2. Прямоугольное сечение.......................................................... 24 10.3.3. Сечение в виде равнобедренного треугольника................... 30 10.3.4. Сечение в виде равнобедренной трапеции.......................... 33
11. К ЗАДАЧЕ № 11 РАСЧЕТ НА УСТОЙЧИВОСТЬ ЦЕНТРАЛЬНО-СЖАТОГО СТЕРЖНЯ................................. 36 11.1. Пример расчета............................................................................ 37 11.2 Расчет с помощью коэффициента формы.................................. 38 11.3 Расчёт методом последовательных приближений................... 39 11.4 Определение величины критической силы и коэффициента запаса устойчивости для подобранного нами стержня....................................................................................... 41 12. К ЗАДАЧЕ № 12. УДАР............................................................... 43 12.1 Расчет балки, изображенной на рисунке 12.1а................. 44 12.2. Расчет балки, изображенной на рис. 12.16............................... 45 ЛИТЕРАТУРА................................................................................ 47
ЗАХАРОВ ВЯЧЕСЛАВ МИХАЙЛОВИЧ
СТРОИТЕЛЬНАЯ МЕХАНИКА
М Е Т О Д И Ч Е С К И Е У К А З А Н И Я
к выполнению контрольных работ по сопротивлению материалов для студентов заочной формы обучения строительных специальностей. Часть2. Сложное сопротивление. Кривой брус. Устойчивость. Удар.
Объем 2,6 Тираж 25 Заказ..... Бесплатно Формат A1 Брянская государственная инженерно-технологическая академия. 241037 г. Брянск, ул. Станке Димитрова, 3, редакционно-издательский отдел.
Отпечатано: лаборатория кафедры "Сопротивление материалов и строительная механика" БГИТА.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.119.14 (0.009 с.) |

 =
=  =0,141·10-3 м = 0,0141 cм.
=0,141·10-3 м = 0,0141 cм. =1 +
=1 +  =24,8
=24,8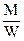 =
=  =
=  = 8,45 МПа (84,5 кгс/см2).
= 8,45 МПа (84,5 кгс/см2). =
= =24,1
=24,1 =
=  ≈ 0,6 МПа (6 кгс/см2);
≈ 0,6 МПа (6 кгс/см2); =
=  =
=  = 2·103 м = 0,2 см.
= 2·103 м = 0,2 см. = 7,19
= 7,19

 при с = 1/2; β = 17/35
при с = 1/2; β = 17/35