
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение эпюры изгибающих моментовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте На расчетной схеме показаны произвольные поперечные сечения на каждом из трех участков. В каждом из сечений проведены две главные центральные оси: Y — вертикальная и X — горизонтальная. В нашем случае, так как нагрузка расположена в вертикальной плоскости, она дает момент лишь вокруг горизонтальной оси Х. Запишем уравнения изгибающих моментов на каждом из участков. Для определенности примем условно за положительный — изгибающий момент, вызывающий растяжение нижних волокон. Участок АВ: (0 ≤ z ≤ 0,8ℓ). MиAB = -qz2/2; при z = 0, MиA = 0. при z = 0,8ℓ, MиB = -q(0,8ℓ)2/2 = - 0,32qℓ 2. Участок ВС: (0 ≤ z ≤,5ℓ). MиBC = - 0,8qℓ∙z. при z = 0, MиB = 0. при z = 0,5ℓ, MиC = - q0,8ℓ∙0,5ℓ =- 0,40qℓ 2. Участок СD: (0≤ z ≤ℓ). MиC D = 0,8qℓ∙(0,4ℓ - z) = 0,32qℓ2 - 0,8qℓ∙z. при z = 0, MиC = 0,32qℓ 2. при z = ℓ, Mи D = 0,32qℓ 2 - 0,8qℓ∙ℓ = - 0,48qℓ 2. По этим данным построена эпюра Ми(рисунок 9.1г). Ее ординаты отложены в плоскости изгиба со стороны растянутого волокна. Из эпюр Мк и Ми видно, что опасным является опорное сечение D, в котором Мк = 0,40 qℓ 2 и Ми =0,48 qℓ 2. На рисунке 9.2а показаны связанные с этими суммарными внутренними силовыми факторами касательные и нормальные напряжения. Даны эпюры распределения этих напряжений по вертикальному диаметру.
Рисунок 2.14
На рисунке 9.26 изображено напряженное состояние в опасных точках сечения 1 и 1'. Величину напряжения при линейном растяжении, эквивалентном по удельной потенциальной энергии изменения формы (четвертой теории прочности) данному упрощенному плоскому напряженному состоянию, можно определить по формуле: σIVрасч = Таким образом, расчетный момент по четвертой теории прочности: M IVрасч = 9.2. Пример «б»» (рисунок 9.3).
Рисунок 9.3. На этом же рисунке показаны размеры участков и координация произвольных поперечных сечений. Запишем выражения изгибающих и крутящих моментов для произвольных поперечных сечений (уравнения Мии Мк ) и их значения для крайних поперечных сечений на каждом из участков. ИЗГИБАЮЩИЕ МОМЕНТЫ MиAB = 0,5qz2/2 – (квадратная парабола); при z = 0, MиA = 0. при z = a, MиB = 0,5qa2 – (растянутые волокна вверху).
MиBС = qa∙z – (прямая); при z = 0, MиВ = 0. при z = a, MиС = qa2 – (растянутые волокна вверху). MиCD = P∙z = qa∙z – (прямая); при z = 0, MиD = 0. при z = a, MиC = qa2 – (растянутые волокна внизу). MиDЕ = P∙z = qa∙z – (прямая); при z = 0, MиЕ = 0. при z = a, MиD = qa2 – (растянутые волокна внизу).
MиKC = qa(0,5a + z) – P(z-a) = 1,5qa2 – (растянутые волокна вверху) – величина постоянная на всем участке.
То, что MиKC =const, можно было видеть и без записи, уравнения, так как обе внешние силы, расположенные по одну сторону от участка КС, равны по величине и противоположно направлены, и поэтому составляют пару сил смоментом относительно оси X,MиKC = qa(0,5a + a) = 1,5 qa2. Эпюра изгибающих моментов построена со стороны растянутых волокон на рисунке 9.3.
КРУТЯЩИЕ МОМЕНТЫ MкAB = 0; MкBС = 0,5qa2; MкCD = qa2; MкDЕ = 0; MкKC = 2qa2. По этим данным на рисунке 9.3. построена эпюра крутящих моментов. Как видно из эпюр, опасными являются все сечения участка КС. MиKC = 1,5qa2; MкKC = 2qa2. Определяем величину расчетного момента по четвертой теории прочности: M IVрасч =
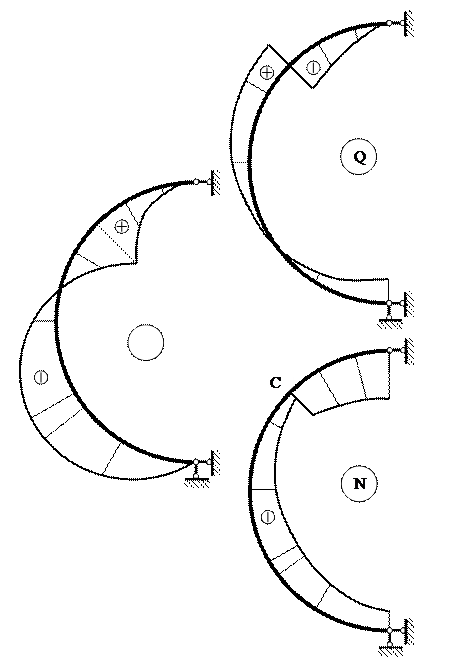
К ЗАДАЧЕ № 10 РАСЧЕТ КРИВОГО БРУСА В задаче рассматривается кривой брус, ось которого очерчена дугой окружности. Требуется построить эпюры внутренних усилий ─ изгибающего момента М,продольной силы Nи поперечной силы Q, а также эпюру нормальных напряжений в опасном поперечном сечении бруса. Будем придерживаться следующего правила знаков: а) положительный изгибающий момент стремится разогнуть ось бруса, т. е. вызывает сжатие в его наружных волокнах; б) положительная поперечная сила стремится повернуть рассматриваемую часть бруса по часовой стрелке (как и в.балках); в) положительная продольная сила вызывает растяжение, т. е. направлена от сечения бруса (как и в прямых стержнях). На рисунке 10.1 показаны положительные направления внутренних сил.
Рисунок 10.1
В качестве примера рассмотрим кривой брус, изображённый на рисунке 10.2. Примем следующие данные: Р=2000 кгс, R = 20 см.
Рисунок 10.2
Определение опорных реакций Разложим силу Р на составляющие по вертикали (Ру)игоризонтали (Рx): Ру = P∙cos 20° = 2000∙0,940 = 1880 кгс; Рx = P∙sin 20° = 2000∙0,342 = 684 кгс; ΣMA = RB∙2R + Px∙R∙sin 45° - Py∙R∙(1+cos 45°) =0; RB = ΣMB = Px∙R∙sin 45° + Py∙R∙(1-cos 45°) - YA∙2R =0; YA = ΣX = XA – Px = 0; XA = Px = 684 кгс. Проверка: ΣY = YA + RB – Py = 516,5 + 1364 – 1880 ≈ 0. Итак: XA = 684 кгс, YA = 516,5 кгс; RB = 1364 кгс.
Построение эпюр M, N и Q 1. Участок АС (0 ≤ φ ≤ 135°).
Рисунок 10.3
б — положительные направления внутренних сил.
На рисунке 10.3а показано поперечное сечение на участке АСи проекции на это сечение и на нормаль к нему всех сил, расположённых по одну сторону от этого сечения, т. е. составляющих реакции на опоре А (ХА и Yа),а также моменты этих сил относительно центра тяжести этого сечения. На рисунке 10.36 показаны положительные направления для М, N и Q. Сопоставляя эти два рисунка, записываем выражения для внутренних сил M = Yа∙R∙(1-cosφ) - ХА∙R∙sinφ. (10.1) N = - XA∙sinφ - YA∙cosφ. (10.2) Q = YA∙ sinφ - XA∙ cosφ. (10.3)
Для упрощения вычислений можно изгибающий момент выразить через продольную силу: M = R∙(YA - YA∙cosφ - XA∙sinφ) = R∙(YA +N). (10.1′) Для того, чтобы не пропустить характерные сечения, в которых внутренние силы принимают экстремальные или нулевые значения, можно выполнить несложное графическое построение (рисунок 10.2). Вначале определена точка D в пересечении линии действия силы Р и реакции RB. Условие равновесия требует, чтобы линия действия реакции RA тоже прошла через точку D. В пересечении линии AD с осью бруса лежит сечение Е,в котором изгибающий момент равен нулю. Проведя перпендикуляр к линии АDиз центра О,определяем положение сечения К,в котором М и Nдолжны иметь экстремальные значения, a Q = 0. Теперь определим положение этих сечений аналитически: а) ME = Yа∙R∙(1-cosφE) - ХА∙R∙sinφE = 0 или (1-cosφE) - 2∙sin2 sin б) QK = YA∙ sinφK - XA∙ cosφK = откуда tgφK = Из построения (рисунок 10.2) видно, что действительно φE = 2 φK. Для построения эпюр М, N и Q на участке АС дадим переменной φ следующие значения: 0°; 30°; 53°; 60°; 90°; 120°; 135°. Результаты вычислений приведены в таблице 10.1 (стр. 30).
Участок ВС (0≤φ≤45°) Положительные направления внутренних сил
Рисунок 10.4
На рисунке 10.4а показаны проекции расположенной по одну сторону от произвольного поперечного сечения силы (RB) на это сечение, на нормаль к нему и момент относительно его центра тяжести. На рисунке 10.46 показаны положительные направления внутренних сил. Сопоставляя эти два рисунка, получаем следующие выражения для внутренних усилий: Q = -RB∙ sinφ; (10.4) N = - RB∙cosφ. (10.5) M = RB∙R∙(1-cosφ) = R∙(RB + N) (10.6)
Таблица 10.2
Ординаты эпюр Q, N и М,приведенных на рисунке 10.5, отложены от оси бруса по нормали к ней. Проверим, правильно ли сопрягаются эпюры в точке С. На эпюре Мскачков не должно быть (в том числе и в сечении С), так как в схеме загружения нет сосредоточенных моментов. Действительно: MCAC = MCBC. На эпюре Q в сечении Сдолжен быть скачок на величину проекции силы Р на плоскость этого сечения: Р∙cos25° = 2000∙0,906 = 1812 кгс. Действительно: QCAC - QCBC = 848-(-964) = 1812 кгс. На эпюре Nв сечении С должен быть скачок на величину проекции силы Рна нормаль к сечению: Р∙sin25° = 2000∙0,423 = 846 кгс. Действительно: NCAC - NCBC = -118-(-964) = 846 кгс. Предполагая, что материал бруса одинаково сопротивляется растяжению и сжатию,6удем cчитать опасным то сечение, в крайних точках которого действуют наибольшие по абсолютной величине нормальные напряжения. Определение напряжений Как видно из эпюр М и N, в нашем примере (в зависимости от формы сечения) опасным может быть одно из трех сечений: сечение К, сечение С участка АС, либо сечение Сучастка ВС. Нормальные напряжения при чистом изгибе кривого бруса (без учета N) определяются по формуле:
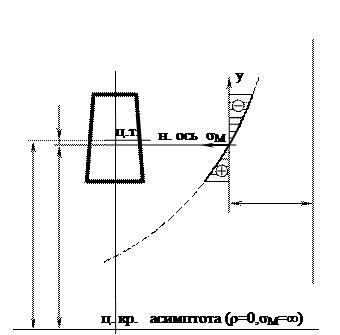
σM = - Здесь обозначено: r ─ радиус кривизны нейтрального слоя; yо = R-г ─ расстояние от нейтрального слоя до центра тяжести сечения; у─ расстояние от нейтрального слоя до точки, в которой определяется напряжение (положительный отсчет ведется в сторону наружных волокон); ρ = г + у— расстояние до этих же точек от центра кривизны. Итак, использование формулы (10.7) требует предварительного определения положения нейтральной оси. Точное значение радиуса кривизны нейтрального слоя можно определить по формулам (10.8), которые для рассматриваемых сечений приводятся ниже. Они получены из равенства: г = Поскольку r мало отличается от R,вычисления по формулам (10.8.) необходимо производить очень тщательно, т. к. иначе нельзя получить с достаточной точностью величину расстояния между нейтральной осью и центром тяжести: y0 = R - r,(10.9) Однако, если брус имеет не очень большую кривизну (примерно, если R>3h),то уоможно получить без предварительного определения r, используя приближенную формулу: yo ≈ Здесь Iх — это момент инерции сечения бруса относительно его главной центральной оси, перпендикулярной плоскости изгиба. Если же брус имеет малую кривизну (примерно R>5h), то нейтральная ось практически сливается с центральной, т. е. yo ≈ 0, и напряжения можно вычислять по обычной формуле для прямого бруса: σM = ─ Эпюра напряжений σМ по формуле (10.7) имеет вид гиперболы сасимптотами ρ = 0 (при σМ → ∞) и σМ = σN = Суммарные напряжения (соответствующие.М и N ) определяются по формуле: σ = σM + σN (10.13)
Рисунок 10. Для получения эпюры суммарных напряжений можно вначале построить гиперболу σM, а затем ось отсчета напряжений сместить в нужную для алгебраического суммирования сторону, как это сделано в приводимых ниже примерах. 10.3.1. Круглое сечение (рисунок 10.7) Диаметр круга ─ d=10 см. Положение нейтральной оси Так как отношение R:d= 20:10 = 2 << 3, то есть рассматриваемый брус имеет очень большую кривизну, то для определения положения нейтральной оси следует пользоваться точной формулой: r = r = yo = R – r = 20 – 19,682 = 0,318 см.
Для сравнения определим уo по приближенной формуле (10.10).
Площадь сечения: F = Центральный момент инерции: Ix = уo ≈
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.009 с.) |


 =
=  =
= 
 =
=  = 0,59qℓ2.
= 0,59qℓ2. На рисунке 9.3 показана расчетная схема стержня, состоящего из пяти участков: АВ, ВС, CD, DE и КС.
На рисунке 9.3 показана расчетная схема стержня, состоящего из пяти участков: АВ, ВС, CD, DE и КС. = 2,29qa2.
= 2,29qa2.


 =
=  = 1364 кгс;
= 1364 кгс; =
=  =516,5 кгс;
=516,5 кгс;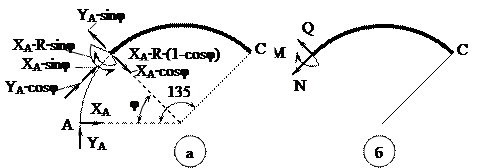
 ∙sinφE = 0,
∙sinφE = 0,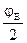 -
-  =1,325,
=1,325,
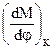 =
=  = 0.
= 0.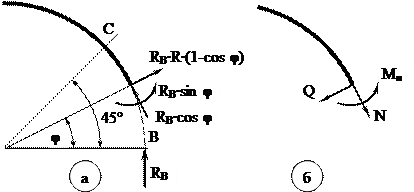
 Для построения эпюр дадим φ следующие значения: 0°; 16°; 30° и 45°. Результаты вычислений приведены в таблице 10.2.
Для построения эпюр дадим φ следующие значения: 0°; 16°; 30° и 45°. Результаты вычислений приведены в таблице 10.2.





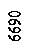
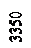





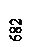



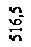














 ∙
∙  =-
=-  (10.7)
(10.7) (10.8.)
(10.8.) (10.10)
(10.10) (10.11)
(10.11)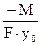 (при y → ∞). Нормальные напряжения, соответствующие продольной силе, распределяются равномерно по сечению и определяются, как и в прямом брусе, по формуле:
(при y → ∞). Нормальные напряжения, соответствующие продольной силе, распределяются равномерно по сечению и определяются, как и в прямом брусе, по формуле: . (10.12)
. (10.12)





 , (10.8)
, (10.8)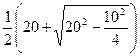 =19,682 см,
=19,682 см, =
=  =78,6 см2.
=78,6 см2. =
=  = 491 см4;
= 491 см4; =
=  = 0,312 см.
= 0,312 см.


