
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Расчет статически неопределимых систем
Общие указания Статически неопределимыми называются системы, силовые факторы в элементах которых определить невозможно при помощи только уравнений статики. В таких системах связей больше, чем необходимо для равновесия. Таким образом, некоторые связи оказываются лишними, а усилие в них – лишними неизвестными. По количеству лишних связей или лишних неизвестных усилий устанавливают степень статической неопределимости системы. Для выявления степени статической неопределимости рам удобно применить формулу
Л = 2Ш + Соп – 3Д,
а для неразрезных балок
Л = Соп – 3.
Установив степень статической неопределимости, можно выбирать основную систему, которая получается из заданной путем освобождения ее от лишних связей (Л). Полученная при этом система должна быть геометрически неизменяемой и статически определимой. Рассмотрим схему расчета статически неопределимых систем методом сил, где в качестве основных неизвестных выбирают усилия лишних связей. Определение лишних неизвестных производят из канонических уравнений, где лишними неизвестными являются силы, представляющие собой реакции отброшенных связей. Число уравнений равно числу отброшенных связей.
1 Для один раз статистически неопределимой системы канонические уравнения имеют вид:
2 Для двух раз статистически неопределимой системы канонические уравнения имеют вид:
Использование основной системы уравнений значительно упрощает решение статически неопределимой задачи. Уравнения метода сил носят стандартный каноничный характер, потому что записываются шаблонно для любой системы. Индивидуальность системы отображается в коэффициентах канонического уравнения
нагрузки или внешнее действие определяются грузовыми коэффициентами Для определения коэффициентов канонических уравнений При подсчете окончательных усилий (M, Q, N) в статически неопределимых системах найденные значения лишних неизвестных следует рассматривать как внешние усилия, прибавленные к основной системе. После того, как лишние неизвестные найдены, решение сводится к расчету основной статически определимой системы на действие внешней нагрузки и ²лишних² неизвестных.
Используя принцип суперпозиций, усилие М можно найти по формуле
Пример 5 Расчет статически неопределимой балки. Для заданной схемы балки (рис. 14) построить эпюры Q и M методом сил. 1 Определяем количество лишних связей:
Л = Соп – 3 = 4 – 3 = 1,
то есть система имеет одну лишнюю связь. 2 Выбираем основную систему, удалив одну связь на опоре В, и заменяем ее неизвестным х1 (рис. 14,а). 3 Строим единичную эпюру 0≤ x ≤ 8 м
4 Строим грузовую эпюру
0≤ x1 ≤ 4 м
4≤ x 2 ≤12 м МX2= - 2∙4 (x2 –2), x2 = 4м, МX2 = -16 кНм, x2 = 12м, МХ2 =-80 кНм.
5 Составляем каноническое уравнение, определяем его коэффициенты и неизвестную реакцию х1.
х1 = 11 кН.
6 Строим исправленную эпюру
7 Строим результирующую эпюру М (рис.14,з), используя зависимость
8 Для построения эпюры Q прикладываем к балке внешнюю нагрузку и найденную неизвестную реакцию х1 = 11 кН (рис. 14,к, 14,л).
0 ≤ х3 ≤ 4 м
4 ≤ х4 ≤ 12 м Qy = + 2 ∙ 4 – 11 = – 3 кН. Пример 6. Расчет статически неопределимой рамы. Для заданной статически неопределимой рамы (рис. 15,а) по методу сил построить эпюры M, Q, N. Расчет выполняем в той же последовательности, что и в примере 5. 1 Степень статической неопределимости: Л = 2Ш + Соп – 3Д = 2 ∙ 0 + 4 – 3 ∙ 1 = 1, то есть система имеет одну лишнюю связь. 2 Выбираем основную систему, удалив одну связь (рис. 15,б). 3 Строим единичную эпюру
Рисунок 15
Рисунок 16
0 ≤ х ≤ 6 м
0 ≤ у1≤ 4 м
0 ≤ х1 ≤ 6 м
0 ≤ у2 ≤ 2 м
0 ≤ у3 ≤ 4 м
Рисунок 17
4 Составляем каноническое уравнение, определяем коэффициенты
5 Строим результирующую эпюру моментов, используя зависимость
Рисунок 18
6 Строим эпюры Q и N (рис. 20). Для этого к основной системе прикладываем внешнюю нагрузку и полученное усилие x1 = 2,6 кН (рис. 19).
0 ≤ у1 ≤ 4 м Q = 0, N = - 2,6 кН.
0 ≤ у2 ≤ 2 м Q = - 5 кН, N = 0 кН.
0 ≤ у3 ≤ 4 м Q = - 5 кН, N = – 12+ 2,6 = -9,4 кН.
0 ≤ х1 ≤ 6 м
N = 0
Рисунок 20
7 Проверка результирующих эпюр из условий равновесия. Эпюра М Эпюры Q и N
Узел 1 Узел 1
∑M1 = + 36 – 10 – 26 =0. ∑X = + 5 – 5 =0, ∑Y = + 9.4 – 9.4 =0.
Узел 2 М = 0. Узел 2
∑Y = + 2.6 – 2.6 =0.
Расчетно-графическое задание №5
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 695; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.130 (0.024 с.) |
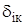 хі+ΔіF=0 или δ11∙ x1 + Δ 1F = 0.
хі+ΔіF=0 или δ11∙ x1 + Δ 1F = 0. .
. и характере лишних неизвестных
и характере лишних неизвестных 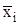 . Характер
. Характер , коэффициентом
, коэффициентом 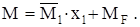
 от
от 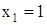 для основной системы (рис. 12,б, 12,в).
для основной системы (рис. 12,б, 12,в). от действия внешней нагрузки для основной системы (рис. 14,г, 14,д).
от действия внешней нагрузки для основной системы (рис. 14,г, 14,д).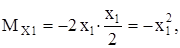

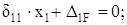
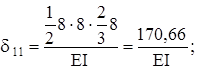



 (рис. 14,ж).
(рис. 14,ж). и грузовую эпюру MF для основной системы (рис. 16,а, 16,б, 17,а, 17,б).
и грузовую эпюру MF для основной системы (рис. 16,а, 16,б, 17,а, 17,б).

 = 1 ∙ x
= 1 ∙ x
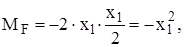



 ,
,  и неизвестное
и неизвестное  :
: ;
; .
. .
. ; x1 = 2,6 кН.
; x1 = 2,6 кН. (рис. 18).
(рис. 18).








