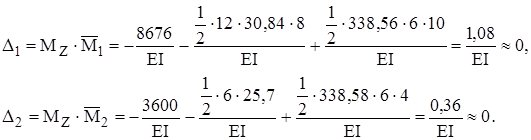Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
К выполнению контрольных заданий по курсу «строительная механика»Содержание книги
Поиск на нашем сайте
ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К выполнению контрольных заданий по курсу «Строительная механика» для студентов русскоязычных групп всех специальностей
Харьков 2013 Министерство образования и науки, молодежи и спорта Украины ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ к выполнению контрольных заданий по курсу «Строительная механика» для студентов русскоязычных групп всех специальностей
Утверждено на заседании кафедры строительной механики. Протокол № 6 от 18.01.2013г.
Харьков 2013 Методические указания к выполнению контрольных заданий по курсу «Строительная механика» для студентов русскоязычных групп всех специальностей / Составители: С.А. Ворончихина, А.В. Медведева, В.Ю. Мирошников, С.В. Олешкевич, А.Б. Савин. - Харьков: ХНУБА, 2013.- 39с.
Кафедра строительной механики
СОДЕРЖАНИЕ ВСТУПЛЕНИЕ...................................................................................................... 3 ТЕМА 1 Расчет многопролетной статически определимой шарнирной балки на действие постоянной нагрузки............................................................ 5 Расчетно - графическое задание №1.................................................... 8 Расчетно - графическое задание №2.................................................... 10 ТЕМА 2 Расчет плоской статически определимой фермы.............................. 14 Расчетно - графическое задание №3.................................................... 15 ТЕМА 3 Расчет трехшарнирной системы......................................................... 18 Расчетно - графическое задание №4.................................................... 21 ТЕМА 4 Расчет статически неопределимых систем……………………......... 23 Расчетно - графическое задание №5.................................................... 29 Расчетно - графическое задание №6.................................................... 36 Список источников информации.......................................................................... 38
ВСТУПЛЕНИЕ Сооружение гражданских и промышленных зданий и вообще все виды инженерно-технической деятельности основываются в первую очередь на расчетах на прочность. Все конструкции во время эксплуатации находятся под действием внешних сил– нагрузок. Нагрузки, которые распределяются между элементами конструкции, вызывают деформации последних и даже могут привести к разрушению или отдельных элементов, или связей между ними. И в первом, и во втором случаях разрушается вся конструкция. Задание инженерного расчета и заключается как раз в том, чтобы подобрать размеры отдельных элементов, определить их необходимое количество и соединить между собой таким образом, чтобы конструкция выдерживала все нагрузки, которые могут возникнуть. Наука, которая изучает методы расчета разных конструкций, имеет общее название «строительная механика». Эта наука изучает вопрос прочности, жесткости и стойкости систем из разных элементов, так или иначе связанных между собой. Статика сооружений является содержанием данных методических указаний. Статика сооружений рассматривает конструкции, которые находятся под действием статических нагрузок, то есть таких, которые передаются на конструкцию, постепенно и плавно растут к своей предельной величине, сохраняя эту величину в течение длительного времени. Методические указания к выполнению контрольных заданий разработаны в соответствии с рабочей программой дисциплины «Строительная механика». Рабочая программа составлена на основе Образовательно-профессиональной программы высшего образования Министерства образования и науки, молодежи и спорта Украины по направлению «Промышленное и гражданское строительство». При изложении материала авторы стремились к тому, чтобы студент, знающий основы теории, мог самостоятельно разобраться в ее приложении к выполнению конкретных заданий. В результате изучения дисциплины «строительная механика» студент должен: 1 Анализировать образование систем из разных сочлененных элементов и исследование их свойств. 2 Определять внутренние усилия в элементах разного типа систем. В сооружениях применяются как статически определимые, так и статически неопределимые системы. Статически определимая система — это система, в которой возможно определить усилие с помощью только уравнений статики твердого тела, а статически неопределимая система — это такая система, в которой невозможно определить усилие посредством только уравнений статики. Статически неопределимые системы называют также системами с лишними неизвестными. Для определения лишних неизвестных составляются дополнительные уравнения, которые основаны на упругих свойствах системы. Основными видами учебной работы по дисциплине являются лекции, практические занятия и самостоятельная работа студента. Для усвоения дисциплины необходимо знание курсов таких дисциплин, как сопротивление материалов и теоретическая механика. Знания и практические навыки, приобретенные при изучении дисциплины, применяются в курсах металлических, деревянных и железобетонных конструкций, оснований и фундаментов. В методических указаниях представлены задания для расчетно — графических работ с необходимыми примерами и пояснениями к их выполнению.
Общие указания Многопролетные статически определимые балки представляют собой комбинированные системы, которые состоят из нескольких простых балок, соединенных шарнирами. Для проведения кинематического анализа расчетной схемы балки определяют степень свободы плоской стержневой системы П. П = 3 Д – 2 Ш - Cоп где Д - количество дисков; Ш - количество простых шарниров; Cоп - количество опорных стержней. При условии: П > 0 – система геометрически изменяема. П ≤ 0 – система геометрически неизменяема. П = 0 – система статически определима. П < 0 – система статически неопределима. Расчет таких балок может быть выполнен с использованием уравнений статики. Эти уравнения составляются не только для всей системы в целом, но и для отдельных ее частей. При составлении уравнений равновесия рационально заданную систему представить так, чтобы наглядным стал порядок опирания одной балки на другую. Многопролетную балку можно представить в виде системы простых однопролетных балок (дисков) с указанием порядка опирания одной балки на другую. Такая схема называется поэтажной или схемой взаимодействия элементов (рис. 1).
Рисунок 1
Поэтажные схемы (рис. 1) наглядно демонстрируют, что расчет сложной консольной балки сводится к расчету нескольких простых однопролетных балок и начинается с верхних балок с последовательным переходом к нижележащим балкам. Во время расчета нижележащих балок следует учитывать не только внешнюю нагрузку, которая действует на них непосредственно, но и давление опор вышележащих балок. В процессе расчета многопролетной балки следует придерживаться установленной последовательности, которая приведена в следующем примере. Пример 1 Для заданной схемы балки (рис. 2): 1 Выполнить кинематический анализ расчетной схемы балки. 2 Построить эпюры Qy и Mz,
1 Выполняем кинематический анализ расчетной схемы балки. Количество степеней свободы плоской стержневой системы определяем по формуле П = 3Д – 2Ш – СОП, где Д = 3 – количество дисков; Ш = 2 – количество простых шарниров; СОП = 5 – количество опорных стержней. П = 3´3 - 2´2 – 5 = 0, то есть необходимое условие геометрической неизменяемости выполняется.
2 Строим схему взаимодействия элементов (поэтажную схему) балки (рис. 2,а). В рассматриваемой расчетной схеме элемент 4-5 геометрически неизменяемый и неподвижный. Для элемента 1-2 в качестве горизонтального опорного стержня выступают элементы 3-4 и 4-5, которые препятствуют его перемещению в горизонтальном направлении. Элемент 3-4 геометрически неизменяемый и неподвижный в силу того, что точки 3 и 4, которые принадлежат элементам 1-2 и 4-5, неподвижные, то есть представленная расчетная схема геометрически неизменяема, неподвижна и статически определима, потому что П = 0.
3 Строим эпюры внутренних усилий Qy и Mz. А) Расчет начинаем с верхней балки 3-4. Опорные реакции R3 = R4 = 10,5 кН. 0≤ x1 ≤ 2,5 м 0≤ x2 ≤ 2,5 м Q1 = +10,5 – 7 = 3,5 кН, Q2 = -10,5 + 7 = -3,5 кН, М1= 10,5 x1 - 7 x1, М2= 10,5 x2 - 7 x2, x1 = 0, М1 = 0, x2 = 0, М2 = 0. x1 = 2,5 м, М1 = 8,75 кНм, x2 = 2,5 м, М2 = 8,75 кНм.
Получив значения Q и M, строим эпюры на общей оси для всей балки (рис. 2,г и 2,д). Б) Далее рассматриваем элемент 4-5. В точке 4 добавляем силу R4 =10,5кН и направляем ее вниз (это давление верхней балки на нижнюю в точке 4). 0≤ x3 ≤ 6 м Q3 = -10,5 кН,
x3 = 6 м, М3 = -63 кНм.
Эпюры для этой балки приведены на (рис. 2,г и 2,д). В) Рассмотрим элемент 1-2-3 и построим для него эпюры Qy и Mz.
Q4 = 10,5 kH,
x4 = 1 м, M4 = -10,5 кНм.
Q5 = 10,5 – 9,95 = 0,55 kH,
x5 = 11 м, M5 = 16 кНм.
x2 = 4 м, Q6 = -8 кН,
x2 = 2 м, M6 = -4 кНм, x2 = 4 м, M6 = -16 кНм. Результирующие эпюры Q и M для заданной балки приведены на рисунках 2,г и 2,д.
Расчетно - графическое задание №1 Пример 2 Для заданной схемы балки (рис. 5): 1 Выполнить кинематический анализ расчетной схемы балки. 2 Построить поэтажную схему балки. 3 Построить эпюры Qy и Mz.
Рисунок 5 1 Выполняем кинематический анализ расчетной схемы балки (рис. 5). П = 3 Д – 2 ш - Coп = 3∙2-2∙1-4 = 0, то есть необходимое условие геометрической неизменяемости выполняется. 2 Строим поэтажную схему балки (рис. 5,а). 3 Строим эпюры внутренних усилий Qy и Mz. А) Расчет начинаем с верхней балки 3-4 (рис. 6). ∑М4 = 0 -R3 ∙11+20∙11∙5∙5-80∙2 = 0 R3 = 95,5кН 0 ≤х1≤11м
Qy = 95,5-20∙х1 = 0 х1 = 4,8м
˟
Б) Дальше рассматриваем элемент 1-2-3. В точке 3 добавляем силу R3 = 95,5кН и направляем ее вниз (это давление верхней балки на нижнюю в точке 3 (рис.7)). ∑Mz = 0; R1∙9-20-95,5∙1-20∙1∙0,5=0; R1 = 13,9кН.
Qy = 0, Mz = +20 кН∙м.
0 ≤ х4≤ 9м Qy = -13,9 кН, Mz = +20-13,9∙ х4, х4 = 0, Mz = + 20 кН∙м, х4 = 9м, Mz = -105,5 кН∙м.
0 ≤ х5≤ 1м Qy =+95,5 +20∙ х5, x5= 0, Qy = +95,5кН, x5= 1м, Qy = +115,5 кН.
По полученным значениям Qy и Mz (рис. 6, 7) строим результирующие эпюры на общей оси для всей балки (рис 5,б; 5,в).
Общие указания Ферма - это стержневая система, которая после введения шарниров во все жесткие узлы будет геометрически неизменяемой системой. В расчетных схемах плоских ферм обычно предусматривается наличие идеальных шарниров, лишенных трения. Сами стержни предусматриваются строго прямолинейными. Оси всех стержней пересекаются в центре узла. Предусматривается также, что нагрузка расположена в узлах. При этих условиях стержни ферм работают на растяжение или сжатие. В шарнирных соединениях элементов моменты в стержнях равняются нулю. Расчет плоских ферм заключается в определении продольных усилий в ее стержнях методом сквозных сечений или методом вырезания узлов. Так как величины внутренних усилий неизвестны не только по величине, но и по направлению, то первоначально их направляют положительно (растянутыми), то есть от узла или от сечения. Если полученное продольное усилие имеет знак «плюс», то стержень растянут, если «минус» - сжат. Для нахождения внутренних усилий методом сквозных сечений разделяют ферму сечением на две части и рассматривают равновесие одной из частей. Этот способ расчета позволяет определить усилие в каждом из стержней при помощи одного уравнения: å Fx = 0, å Fу = 0 или å М = 0 (это точка пересечения осей двух стержней в данном сечении). При определении усилий методом вырезания узлов усилия определяют при помощи уравнения å Fx = 0 или å Fу = 0, при этом определять усилия надо начинать с узла, в котором сходиться не более двух стержней.
Пример 3 Определить усилия в стержнях второй панели фермы, изображенной на рисунке 8. Для определения усилий используем метод сквозных сечений и вырезания узлов.
1 Определяем опорные реакции.
H1 – 10 = 0 H1 = 10 кН.
2 Определяем усилия. Для этого проводим сечение m-m. Рассматриваем левую часть (рис.8,б). Неизвестные усилия направляем в положительном направлении (то есть от узла).
N9-8 ∙ 2 + 12,5 ∙4 = 0 N9-8 = -25 кН. Знак «минус» указывает на то, что усилие N9-8 не растягивающее, а сжимающее.
Знак «плюс» указывает на то, что стержень
Для определения усилий в стержне
Расчетно-графическое задание №3 Общие указания Расчет трехшарнирной системы будем рассматривать на примере расчета трехшарнирной рамы (рис.10). Трехшарнирная рама состоит из двух дисков: АС и ВС, которые соединены посредством одного шарнира С друг с другом и двумя шарнирами: А и В с основанием. Основание может рассматриваться как третий диск. Следовательно трехшарнирная рама представляет собой соединение трех дисков посредством трех шарниров, которые не расположены на одной прямой.
Реакции опор А и В трехшарнирной рамы характеризуются каждая двумя параметрами: величиной и направлением (горизонтальной – НА и НВ; вертикальной – RА и RВ). Исходя из этого, опорные реакции трехшарнирной рамы характеризуются четырьмя параметрами (рис. 10). Они могут быть определены из трех уравнений равновесия всех сил, которые действуют на систему (включая и опорные реакции). А также четвертого уравнения, которое выражает равенство нулю момента всех сил, которые действуют на левую или правую часть системы, относительно шарнира С. Из этого следует, что трехшарнирная рама является статически определимой. Во время действия на трехшарнирную систему вертикальной нагрузки горизонтальные составляющие НА и НВ не равняются нулю. Для определения реакций составляют следующие уравнения равновесия:
∑МВ = 0 > RА, ∑МА = 0 > RВ, ∑МСлевых сил = 0 > НА, ∑МСправых сил = 0 > НВ. Внутренними усилиями, которые возникают в поперечных сечениях рамы, являются изгибающие моменты М, поперечные силы Q и продольные силы N.
При определении внутренних усилий М и Q и построения эпюр этих усилий используют правило знаков как и для балок, а продольная сила N считается положительной при растяжении, а отрицательной при сжатии. Эпюры для трехшарнирных рам строятся на схемах рамы отдельно для каждого внутреннего усилия. Проверка правильности построенных эпюр М, Q, N выполняется, исходя из условий равновесия в жестких узлах рамы. Пример 4 Для заданной схемы трехшарнирной рамы с нагрузками F и g (рис. 11): 1 Определить реакции опорных связей с последующей проверкой. 2 Составить уравнение внутренних усилий и построить эпюры М, Q, N. 3 Выполнить проверку решения.
1 Определяем опорные реакции: А) вертикальные RА и RВ
RВ = -34кН. Знак “минус” указывает, что направление реакции RВ нужно изменить на противоположный, то есть вниз ∑МВ=0 -RА∙6+ F∙ 7,8+ g RА= 64кН. Проверка: ∑у = 0; +64-30-34 = = 0. Б) Определяем горизонтальные реакции НА и НВ.
∑МслеваС = 0; + F∙7,8 - RА ∙6 + +НА∙5 =0, НА = 30кН. ∑МсправаС = 0; НВ ∙5 - g∙5∙2,5 = 0, НВ = 30кН. Проверка: ∑х = 0; +30+30 -12∙5=0.
2 Строим эпюры М, Q, N, используя метод сечений. 0 ≤х1≤5м Q = - НА = -30кН,
N = -RА = -64 кН.
0 ≤х2≤1,8м Q = - F = -30кН,
N = 0.
1,8м ≤х3≤7,8м Q = RА - F = 34кН,
N = - НА = -30кН.
0 ≤х4≤5м
N = RВ = 34кН.
По полученным значениями М, Q, N строим эпюры (рис.12).
Рисунок 12 3. Выполняем статическую проверку эпюр. Для этого вырезаем узлы 1 и 2.
Эпюра М ∑М1 = 0; +54+150-204 = 0,
Эпюра Q и N
Расчетно-графическое задание №4 Расчет трехшарнирной рамы Для заданной рамы (рис. 13) с нагрузками и размерами, указанными в таблице 4 и выбранными согласно с индивидуальным шифром: 1 Определить реакции опорных связей со следующей их проверкой. 2 Составить уравнение внутренних усилий и построить эпюры М, Q, N. 3 Провести проверку решения.
Таблица 4. Исходные данные для рамы.
Общие указания Статически неопределимыми называются системы, силовые факторы в элементах которых определить невозможно при помощи только уравнений статики. В таких системах связей больше, чем необходимо для равновесия. Таким образом, некоторые связи оказываются лишними, а усилие в них – лишними неизвестными. По количеству лишних связей или лишних неизвестных усилий устанавливают степень статической неопределимости системы. Для выявления степени статической неопределимости рам удобно применить формулу
Л = 2Ш + Соп – 3Д,
а для неразрезных балок
Л = Соп – 3.
Установив степень статической неопределимости, можно выбирать основную систему, которая получается из заданной путем освобождения ее от лишних связей (Л). Полученная при этом система должна быть геометрически неизменяемой и статически определимой. Рассмотрим схему расчета статически неопределимых систем методом сил, где в качестве основных неизвестных выбирают усилия лишних связей. Определение лишних неизвестных производят из канонических уравнений, где лишними неизвестными являются силы, представляющие собой реакции отброшенных связей. Число уравнений равно числу отброшенных связей.
1 Для один раз статистически неопределимой системы канонические уравнения имеют вид:
2 Для двух раз статистически неопределимой системы канонические уравнения имеют вид:
Использование основной системы уравнений значительно упрощает решение статически неопределимой задачи. Уравнения метода сил носят стандартный каноничный характер, потому что записываются шаблонно для любой системы. Индивидуальность системы отображается в коэффициентах канонического уравнения
нагрузки или внешнее действие определяются грузовыми коэффициентами Для определения коэффициентов канонических уравнений При подсчете окончательных усилий (M, Q, N) в статически неопределимых системах найденные значения лишних неизвестных следует рассматривать как внешние усилия, прибавленные к основной системе. После того, как лишние неизвестные найдены, решение сводится к расчету основной статически определимой системы на действие внешней нагрузки и ²лишних² неизвестных. Используя принцип суперпозиций, усилие М можно найти по формуле
Пример 5 Расчет статически неопределимой балки. Для заданной схемы балки (рис. 14) построить эпюры Q и M методом сил. 1 Определяем количество лишних связей:
Л = Соп – 3 = 4 – 3 = 1,
то есть система имеет одну лишнюю связь. 2 Выбираем основную систему, удалив одну связь на опоре В, и заменяем ее неизвестным х1 (рис. 14,а). 3 Строим единичную эпюру 0≤ x ≤ 8 м
4 Строим грузовую эпюру
0≤ x1 ≤ 4 м
4≤ x 2 ≤12 м МX2= - 2∙4 (x2 –2), x2 = 4м, МX2 = -16 кНм, x2 = 12м, МХ2 =-80 кНм.
5 Составляем каноническое уравнение, определяем его коэффициенты и неизвестную реакцию х1.
х1 = 11 кН.
6 Строим исправленную эпюру
7 Строим результирующую эпюру М (рис.14,з), используя зависимость
8 Для построения эпюры Q прикладываем к балке внешнюю нагрузку и найденную неизвестную реакцию х1 = 11 кН (рис. 14,к, 14,л).
0 ≤ х3 ≤ 4 м
4 ≤ х4 ≤ 12 м Qy = + 2 ∙ 4 – 11 = – 3 кН. Пример 6. Расчет статически неопределимой рамы. Для заданной статически неопределимой рамы (рис. 15,а) по методу сил построить эпюры M, Q, N. Расчет выполняем в той же последовательности, что и в примере 5. 1 Степень статической неопределимости: Л = 2Ш + Соп – 3Д = 2 ∙ 0 + 4 – 3 ∙ 1 = 1, то есть система имеет одну лишнюю связь. 2 Выбираем основную систему, удалив одну связь (рис. 15,б). 3 Строим единичную эпюру
Рисунок 15
Рисунок 16
0 ≤ х ≤ 6 м
0 ≤ у1≤ 4 м
0 ≤ х1 ≤ 6 м
0 ≤ у2 ≤ 2 м
0 ≤ у3 ≤ 4 м
Рисунок 17
4 Составляем каноническое уравнение, определяем коэффициенты
5 Строим результирующую эпюру моментов, используя зависимость
Рисунок 18
6 Строим эпюры Q и N (рис. 20). Для этого к основной системе прикладываем внешнюю нагрузку и полученное усилие x1 = 2,6 кН (рис. 19).
0 ≤ у1 ≤ 4 м Q = 0, N = - 2,6 кН.
0 ≤ у2 ≤ 2 м Q = - 5 кН, N = 0 кН.
0 ≤ у3 ≤ 4 м Q = - 5 кН, N = – 12+ 2,6 = -9,4 кН.
0 ≤ х1 ≤ 6 м
N = 0
Рисунок 20
7 Проверка результирующих эпюр из условий равновесия. Эпюра М Эпюры Q и N
Узел 1 Узел 1
∑M1 = + 36 – 10 – 26 =0. ∑X = + 5 – 5 =0, ∑Y = + 9.4 – 9.4 =0.
Узел 2 М = 0. Узел 2
∑Y = + 2.6 – 2.6 =0.
Расчетно-графическое задание №5 Пример 7 Расчет статически неопределимой рамы методом сил. Для заданной статически неопределимой рамы (рис. 23) построить эпюры M, Q, N.
Рисунок 23 Рисунок 24
1 Степень статической неопределимости: Л = 2Ш + Сoп -3Д = 2∙0+5-3∙1 = 2, то есть система имеет две лишних связи. 2 Выбираем основную систему, удалив две связи (рис.24). 3 Строим единичные эпюры
0 ≤х≤12м
0 ≤х1≤6м
Рисунок 27
0 ≤х2≤6м МF = +10кН∙м,
0 ≤х3≤4м
0 ≤х4≤6м
4 Составляем канонические уравнения, определяем коэффициенты: ,
.
5 Строим результирующую эпюру моментов МF,(рис. 28, 29), используя зависимость:
Рисунок 28
Рисунок 29
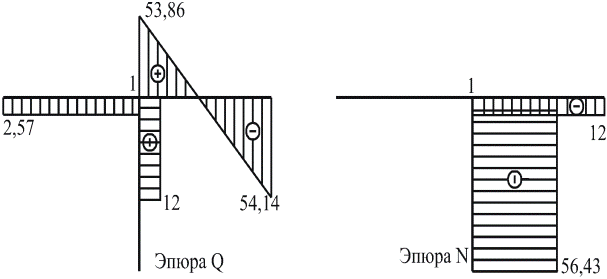
6 Строим эпюры Qy и N (рис. 31). Для этого к основной системе добавляем внешнюю нагрузку и полученные усилия (рис. 30) х1 = -2,57 кН, х2=56,43кН.
Рисунок 30 0 ≤х1≤6м0 ≤х2≤4м Q = - 2,57 кН, Q = 0, N = 0. N = - 56,43 кН.
0 ≤х3≤4м0 ≤х4≤6м
N = - 56,47 кН. N = – 12 кН.
Рисунок 31
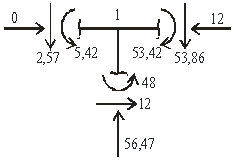
7 Проверка результирующих эпюр из условий: А) равновесия в узле 1:
∑М1 = 0; +5,42+48-53,42=0,
∑у = 0; -2,57-53,86+56,47=0,
∑х = 0; +12-12 = 0.
Б) перемещений:
Расчетно-графическое задание № 6 Навчальне видання Методичні вказівки до виконання контрольних завдань з курсу «Будівельна механіка» для студентів російськомовних груп усіх спеціальностей
Укладачі: Ворончіхіна Світлана Олексіївна Медведєва Алла Василівна Мірошніков Віталій Юрійович Олешкевич Сергій Вікентійович Савін Олександр Борисович
Відповідальний за випуск В.Б. Гриньов
Редактор В. І. Пуцик
План Формат 60х84 1/16. Папір друк. №2. Підп. до друку Обл.-вид.арк. Безкоштовно. Надруковано на ризографі. Умов.друк.арк. Тираж 50 прим. Зам.№
ХНУБА, 61002, Харків, вул. Сумська, 40
Підготовлено та надруковано РВВ Харківського націонал
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 832; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.207.11 (0.01 с.) |


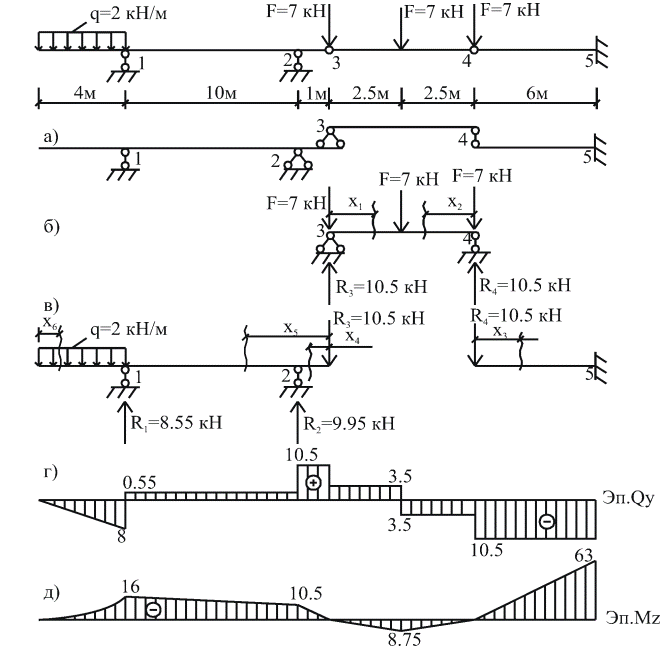 Рисунок 2
Рисунок 2 М3= -10,5 x3, x3 = 0, М3 = 0,
М3= -10,5 x3, x3 = 0, М3 = 0,





 M4 = -10,5 ∙ x4 x4 = 0, M4 = 0,
M4 = -10,5 ∙ x4 x4 = 0, M4 = 0,
 M5 = -10,5 ∙ x5 + 9,95 (x5 – 1), x5 = 1, M5 = -10,5 кНм,
M5 = -10,5 ∙ x5 + 9,95 (x5 – 1), x5 = 1, M5 = -10,5 кНм,
 M6 = -2 ∙ x6 (x6 / 2), x2 = 0, M6 = 0 кНм,
M6 = -2 ∙ x6 (x6 / 2), x2 = 0, M6 = 0 кНм,


 = 95,5 ∙ 4,8 – 20 ˟
= 95,5 ∙ 4,8 – 20 ˟ = +228 кН∙м.
= +228 кН∙м. 0 ≤ х3≤ 2м
0 ≤ х3≤ 2м
 ,
, ,
,  кН.
кН. ,
, ,
,  кН.
кН.
 ,
,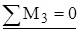 ,
, ,
,  ,
,  кН.
кН.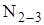 растянут.
растянут. ,
,  ,
,  кН.
кН. вырезаем узел 9 (рис.8,в).
вырезаем узел 9 (рис.8,в). ,
,  кН.
кН. Такое соединение, как известно, является геометрически неизменяемым.
Такое соединение, как известно, является геометрически неизменяемым. ∑МА=0; + F∙1,8+ g
∑МА=0; + F∙1,8+ g 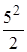 +RВ ∙6 =0,
+RВ ∙6 =0,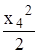
 Епюра М Епюра Q Епюра N
Епюра М Епюра Q Епюра N


 Рисунок 13
Рисунок 13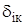 хі+ΔіF=0 или δ11∙ x1 + Δ 1F = 0.
хі+ΔіF=0 или δ11∙ x1 + Δ 1F = 0. .
. и характере лишних неизвестных
и характере лишних неизвестных 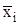 . Характер
. Характер , коэффициентом
, коэффициентом 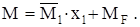
 от
от 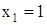 для основной системы (рис. 12,б, 12,в).
для основной системы (рис. 12,б, 12,в). от действия внешней нагрузки для основной системы (рис. 14,г, 14,д).
от действия внешней нагрузки для основной системы (рис. 14,г, 14,д).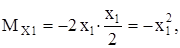

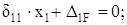
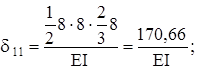



 (рис. 14,ж).
(рис. 14,ж). и грузовую эпюру MF для основной системы (рис. 16,а, 16,б, 17,а, 17,б).
и грузовую эпюру MF для основной системы (рис. 16,а, 16,б, 17,а, 17,б).

 = 1 ∙ x
= 1 ∙ x
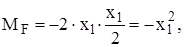



 ,
,  и неизвестное
и неизвестное  :
: ;
; .
. .
. ; x1 = 2,6 кН.
; x1 = 2,6 кН. (рис. 18).
(рис. 18).






 (рис. 25,26) и грузовую эпюру МF для основной системы (рис.27).
(рис. 25,26) и грузовую эпюру МF для основной системы (рис.27). Рисунок 25
Рисунок 25 = 1∙х
= 1∙х
 Рисунок 26
Рисунок 26 = 1∙х1
= 1∙х1

 и неизвестные
и неизвестные 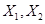 :
: ,
, ,
, ,
, ,
,
 .
.

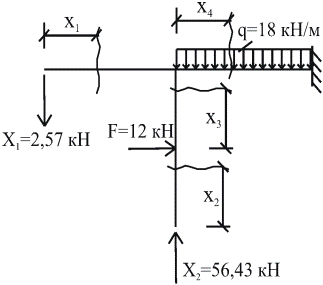
 Q = - 12 кН,
Q = - 12 кН,