
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Расчет многопролетной статически определимой шарнирной балки на действие постоянной нагрузки
Общие указания Многопролетные статически определимые балки представляют собой комбинированные системы, которые состоят из нескольких простых балок, соединенных шарнирами. Для проведения кинематического анализа расчетной схемы балки определяют степень свободы плоской стержневой системы П. П = 3 Д – 2 Ш - Cоп где Д - количество дисков; Ш - количество простых шарниров; Cоп - количество опорных стержней. При условии: П > 0 – система геометрически изменяема. П ≤ 0 – система геометрически неизменяема. П = 0 – система статически определима. П < 0 – система статически неопределима. Расчет таких балок может быть выполнен с использованием уравнений статики. Эти уравнения составляются не только для всей системы в целом, но и для отдельных ее частей. При составлении уравнений равновесия рационально заданную систему представить так, чтобы наглядным стал порядок опирания одной балки на другую. Многопролетную балку можно представить в виде системы простых однопролетных балок (дисков) с указанием порядка опирания одной балки на другую. Такая схема называется поэтажной или схемой взаимодействия элементов (рис. 1).
Рисунок 1
Поэтажные схемы (рис. 1) наглядно демонстрируют, что расчет сложной консольной балки сводится к расчету нескольких простых однопролетных балок и начинается с верхних балок с последовательным переходом к нижележащим балкам. Во время расчета нижележащих балок следует учитывать не только внешнюю нагрузку, которая действует на них непосредственно, но и давление опор вышележащих балок. В процессе расчета многопролетной балки следует придерживаться установленной последовательности, которая приведена в следующем примере. Пример 1 Для заданной схемы балки (рис. 2): 1 Выполнить кинематический анализ расчетной схемы балки. 2 Построить эпюры Qy и Mz,
1 Выполняем кинематический анализ расчетной схемы балки. Количество степеней свободы плоской стержневой системы определяем по формуле П = 3Д – 2Ш – СОП, где Д = 3 – количество дисков; Ш = 2 – количество простых шарниров; СОП = 5 – количество опорных стержней. П = 3´3 - 2´2 – 5 = 0, то есть необходимое условие геометрической неизменяемости выполняется.
2 Строим схему взаимодействия элементов (поэтажную схему) балки (рис. 2,а). В рассматриваемой расчетной схеме элемент 4-5 геометрически неизменяемый и неподвижный. Для элемента 1-2 в качестве горизонтального опорного стержня выступают элементы 3-4 и 4-5, которые препятствуют его перемещению в горизонтальном направлении. Элемент 3-4 геометрически неизменяемый и неподвижный в силу того, что точки 3 и 4, которые принадлежат элементам 1-2 и 4-5, неподвижные, то есть представленная расчетная схема геометрически неизменяема, неподвижна и статически определима, потому что П = 0.
3 Строим эпюры внутренних усилий Qy и Mz. А) Расчет начинаем с верхней балки 3-4. Опорные реакции R3 = R4 = 10,5 кН. 0≤ x1 ≤ 2,5 м 0≤ x2 ≤ 2,5 м Q1 = +10,5 – 7 = 3,5 кН, Q2 = -10,5 + 7 = -3,5 кН, М1= 10,5 x1 - 7 x1, М2= 10,5 x2 - 7 x2, x1 = 0, М1 = 0, x2 = 0, М2 = 0. x1 = 2,5 м, М1 = 8,75 кНм, x2 = 2,5 м, М2 = 8,75 кНм.
Получив значения Q и M, строим эпюры на общей оси для всей балки (рис. 2,г и 2,д). Б) Далее рассматриваем элемент 4-5. В точке 4 добавляем силу R4 =10,5кН и направляем ее вниз (это давление верхней балки на нижнюю в точке 4). 0≤ x3 ≤ 6 м Q3 = -10,5 кН,
x3 = 6 м, М3 = -63 кНм.
Эпюры для этой балки приведены на (рис. 2,г и 2,д). В) Рассмотрим элемент 1-2-3 и построим для него эпюры Qy и Mz.
Q4 = 10,5 kH,
x4 = 1 м, M4 = -10,5 кНм.
Q5 = 10,5 – 9,95 = 0,55 kH,
x5 = 11 м, M5 = 16 кНм.
x2 = 4 м, Q6 = -8 кН,
x2 = 2 м, M6 = -4 кНм, x2 = 4 м, M6 = -16 кНм. Результирующие эпюры Q и M для заданной балки приведены на рисунках 2,г и 2,д.
Расчетно - графическое задание №1
|
|||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 1693; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.208.72 (0.007 с.) |
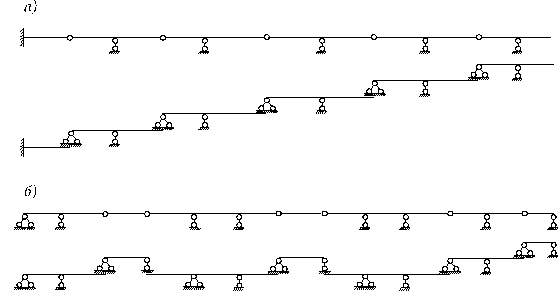
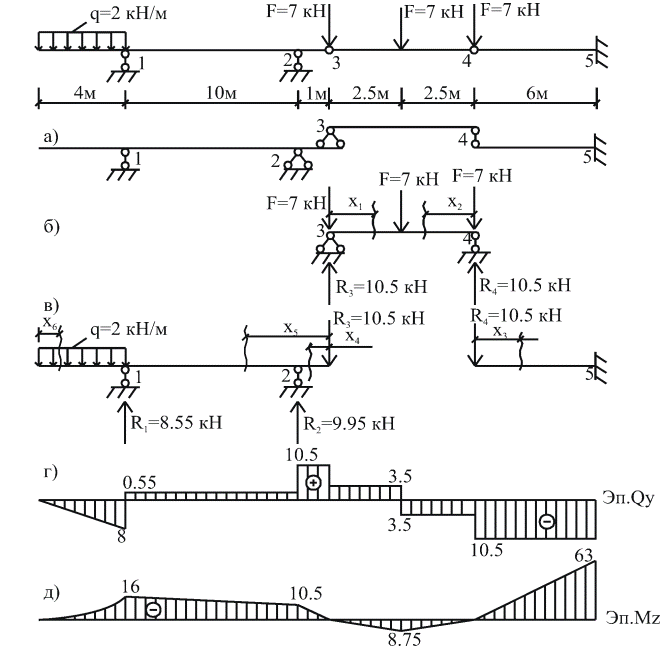 Рисунок 2
Рисунок 2 М3= -10,5 x3, x3 = 0, М3 = 0,
М3= -10,5 x3, x3 = 0, М3 = 0,

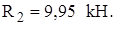




 M4 = -10,5 ∙ x4 x4 = 0, M4 = 0,
M4 = -10,5 ∙ x4 x4 = 0, M4 = 0,
 M5 = -10,5 ∙ x5 + 9,95 (x5 – 1), x5 = 1, M5 = -10,5 кНм,
M5 = -10,5 ∙ x5 + 9,95 (x5 – 1), x5 = 1, M5 = -10,5 кНм,
 M6 = -2 ∙ x6 (x6 / 2), x2 = 0, M6 = 0 кНм,
M6 = -2 ∙ x6 (x6 / 2), x2 = 0, M6 = 0 кНм,


