
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор регрессионной математической моделиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Выбор регрессионной математической модели требует глубокого знания объекта исследования и методов математического моделирования. При этом целью исследования является проникновение в те процессы, которые исследователю неизвестны. Под регрессионной математической моделью понимают зависимость функции отклика от варьируемых факторов:
Выбрать модель – это значит определить вид этой функции, записать ее уравнение. Для выбранной модели необходимо поставить специально спланированный эксперимент, чтобы найти оценки коэффициентов регрессии. Планирование экспериментов производится поэтапно. Не всегда сразу понятно, как получить конечный результат – регрессионную модель в явном виде, то есть с конкретными значениями коэффициентов регрессии. Обычно возникает необходимость действовать методом «проб и ошибок». На начальном этапе необходимо выбрать факторы, которые в наибольшей степени влияют на выходную величину. Для этого возможно необходимо провести так называемый отсеивающий эксперимент. Этот эксперимент должен выявить те факторы, которые действительно существенно влияют на выходную величину. Количество факторов не должно быть слишком большим, например, больше пятнадцати. Большое количество факторов приведет нас к необходимости поставить соответственно большое количество экспериментов. Это может оказаться трудно выполнимой задачей, особенно в том случае, когда каждый эксперимент связан с большими затратами материальных, временных и других ресурсов. Далее для каждого фактора необходимо выбрать диапазон его возможных значений, то есть область определения факторов. Например, для эксперимента с двумя факторами область определения факторов будет иметь вид, показанный на рисунке 3.1.
Рисунок 3.1. Факторное пространство для двух факторов
Чтобы выбрать конкретный вид математической модели, необходимо выдвинуть конкретные требования. Этими требованиями могут быть адекватность и простота. Адекватность – это возможность вычислять значения функции отклика по регрессионной математической модели в заданной области определения факторов с требуемой точностью без постановки экспериментов. Простота математической модели объясняется необходимостью реализуемости вычислений по данной модели.
3.4. Полный факторный эксперимент (ПФЭ) [1, 3, 5, 24, 26, 36]
Постановка полного факторного эксперимента предполагает наличие априорной (до проведения эксперимента) информации о поведении объекта исследования. Эта информация должна быть добыта в результате наблюдения поведения объекта исследования или получена из источников предыдущих исследований. Выбор областей варьирования факторов может быть сделан на основе глубокого изучения объекта исследования. Этот вопрос решается не просто. Это искусство и опыт экспериментатора. Выбор основного уровня плана эксперимента, полученный в результате изучения априорной информации, можно рассматривать как комбинацию значений факторов в многомерной факторной гиперплоскости исходной точке для построения плана эксперимента. Каждая комбинация значений факторов может являться исходной точкой для построения плана эксперимента. Эта точка может быть использована в качестве исходной точки для построения плана эксперимента. Ее можно назвать основным (нулевым) уровнем. Построение плана эксперимента сводится к выбору экспериментальных точек, симметричных относительно нулевого уровня. Выбор наилучших условий проведения опытов ложится на самого исследователя, который хорошо знает исследуемый объект (процесс). Если имеются сведения о координатах наилучшей точки и нет информации о границах определения факторов, то есть смысл принять эту точку в качестве основного уровня. Аналогичное решение принимается, если границы определены и наилучшие условия находятся внутри области определения факторов. В том случае, если центр эксперимента лежит на границе или близко к ней, необходимо основной уровень выбирать на некотором расстоянии от наилучших условий. Интервалом варьирования фактора называется число, которое определяет расстояние между нижним и верхним пределами варьирования
Рисунок 3.2. Область варьирования факторов
Значения факторов выбираются таким образом, чтобы нижний уровень соответствовал значению
где
Рисунок 3.3. Область варьирования факторов в нормализованных значениях
Интервал варьирования не может быть меньше ошибки, с которой экспериментатор фиксирует уровень фактора Размер интервалов варьирования факторов выбирается из возможного поведения выходной величины, полученной по результатам однофакторных экспериментов. Обычно вначале выбирается линейная регрессионная модель, в которой выходная величина линейно зависит от каждого фактора. В каждой конкретной задаче интервалы варьирования зависят от характера поверхности отклика и от точности фиксирования факторов. Полный факторный эксперимент предполагает, что каждый фактор варьируется на двух уровнях (минимальном и максимальном). Число основных опытов в этом плане равно Матрица плана полного факторного эксперимента с двумя факторами Таблица 3.1
Матрица составлена в нормализованных значениях факторов. Минимальное значение Натуральные значения факторов обозначаются как Переход от натуральных значений к нормализованным значениям факторов осуществляется по формулам:
Здесь
Значения
На рисунке 3.4 показана факторная плоскость с натуральными значениями двух факторов
Рисунок 3.4. Полный факторный план с натуральными значениями факторов
Переход к нормализованным значениям факторов дает ряд существенных преимуществ. Система координат для нормализованных значений безразмерная, поэтому при необходимости учета влияния взаимодействия факторов на выходную величину не надо думать о совместимости их размерностей. Кроме того, при этом влияние каждого фактора на выходную величину не зависит от величин натуральных значений факторов, поскольку все они находятся в одном диапазоне от Точка плана эксперимента с координатами План эксперимента с тремя факторами может быть геометрически представлен в нормализованных значениях в виде куба, рисунок 3.5.
Рисунок 3.5. Геометрическая интерпретация полного факторного эксперимента с тремя факторами
Матрица планирования эксперимента с тремя факторами с фиктивной переменной
Таблица 3.2
Матрица планирования полного факторного эксперимента обладает следующими свойствами.
· Симметричность относительно центра плана эксперимента
· Нормированность
· Ортогональность
Здесь
Коэффициенты уравнения регрессии по методу наименьших квадратов вычисляются следующим образом:
Матрица моментов
Учитывая свойства матрицы планирования, получим:
Поскольку матрица моментов
Вектор
Таким образом, получим уравнение:
Следовательно, любой коэффициент уравнения регрессии
Пример. Пусть поставлен полный факторный эксперимент с двумя факторами. Матрица плана эксперимента будет иметь вид
(3.14)
Транспонированная матрица плана эксперимента будет иметь вид
Матрица моментов
Обратная матрица
Вектор
Вектор коэффициентов
Таким образом, коэффициенты можно вычислить по следующим формулам:
|
||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 482; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.009 с.) |




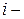 го фактора
го фактора  , рисунок 3.2.
, рисунок 3.2.
 , а верхний
, а верхний  +1. Это позволяет избавиться от необходимости учитывать размерности факторов, а также для упрощения условий проведения эксперимента. На рис. 3.3 показана факторная плоскость в нормализованных значениях факторов (
+1. Это позволяет избавиться от необходимости учитывать размерности факторов, а также для упрощения условий проведения эксперимента. На рис. 3.3 показана факторная плоскость в нормализованных значениях факторов ( ). Для нормализованного значения фактора
). Для нормализованного значения фактора 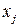 будем иметь выражение:
будем иметь выражение: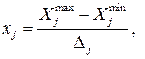 (3.1)
(3.1) максимальное значение
максимальное значение 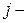 го фактора,
го фактора,  минимальное значение
минимальное значение  диапазон изменения
диапазон изменения 
 Неопределенность внутри области определения факторов может быть устранена при помощи интуитивных решений.
Неопределенность внутри области определения факторов может быть устранена при помощи интуитивных решений. Здесь
Здесь  число факторов, 2-число уровней
число факторов, 2-число уровней 
 представлена в таблице 3.1.
представлена в таблице 3.1.
 Нормализованные значения факторов обозначаются как
Нормализованные значения факторов обозначаются как 
 (3.2)
(3.2)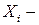 натуральное значение
натуральное значение  значение
значение  половина диапазона варьирования
половина диапазона варьирования 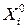 и
и 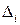 рассчитываются по следующим формулам:
рассчитываются по следующим формулам: (3.3)
(3.3) и
и  .
.
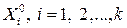 называется центром плана.
называется центром плана.
 для всех основных опытов полного факторного плана приведена в таблице 3.2.
для всех основных опытов полного факторного плана приведена в таблице 3.2.
 (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6)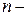 число основных опытов в матрице планирования.
число основных опытов в матрице планирования. (3.7)
(3.7) будет иметь вид
будет иметь вид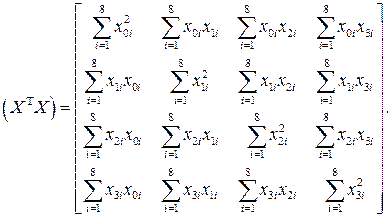 (3.8)
(3.8) (3.9)
(3.9) также будет диагональной
также будет диагональной
 (3.10)
(3.10) будет иметь вид
будет иметь вид
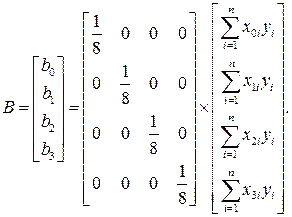 (3.12)
(3.12) (3.13)
(3.13)
 . (3.15)
. (3.15) (3.16)
(3.16)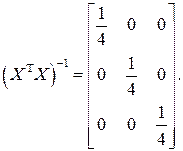 (3.17)
(3.17)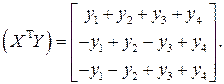 (3.18)
(3.18)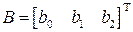 будет вычисляться следующим образом:
будет вычисляться следующим образом: (3.19)
(3.19)



