
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятность, случайные события и случайные величиныСодержание книги
Поиск на нашем сайте
Случайным событием А называется такое событие при проведении эксперимента, которое может произойти или нет [11]. Поэтому со случайным событием А связывается понятие вероятности
Вероятность появления случайного события
Вероятность характеризует объективную возможность появления данного случайного события или данного значения случайной величины в эксперименте. Если случайное событие А происходит в каждом опыте, то есть Пример. Пусть используется некоторый прибор для измерения шероховатости поверхности пиломатериалов. Шкала прибора показана на рисунке 1.2.
Рисунок 1.2. Шкала прибора для измерения шероховатости
Вероятность того, что стрелка прибора будет находиться в интервале Такое вычисление вероятности (1.1) определяется как свойство «статистической устойчивости частот», то есть это означает, что при увеличении количества проведенных экспериментов
где
Запись (1.3) означает, что Случайная величина – это величина, которая в результате опыта принимает значение, которое нельзя предсказать исходя из условий опыта. Случайная величина может принимать любое значение из множества своих возможных значений даже при неизменных условиях проведения опыта, причем, заранее неизвестно какое именно. Изменение случайной величины от опыта к опыту связано с наличием неучтенных факторов (случайных факторов). Различают непрерывные и дискретные случайные величины. · Непрерывная случайная величина заполняет некоторый интервал. Например, температура или влажность. · Дискретная случайная величина принимает отдельные значения. Например, количество сучков на доске. Множество всех возможных значений случайной величины образует генеральную статистическую совокупность. Генеральная статистическая совокупность может быть либо очень большой, либо бесконечно большой. Часть генеральной статистической совокупности называется выборочной статистической совокупностью или выборкой.
Теорема Бернулли
Согласно теореме Бернулли справедливо следующее неравенство
где Вероятность того, что предел разности между относительной частотой
(1.5)
Аксиомы Колмогорова
1. 2. 3. 4. Сложение вероятностей независимых случайных событий имеет вид:
где 5. Произведение независимых случайных событий описывается уравнением
Если случайные события
где Сумма вероятностей
|
||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 553; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 . Вероятность вычисляется как отношение числа экспериментов
. Вероятность вычисляется как отношение числа экспериментов  , в котором произошло событие А, к общему числу экспериментов
, в котором произошло событие А, к общему числу экспериментов 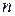 при
при  , то есть
, то есть (1.1)
(1.1) (1.2)
(1.2) то это достоверное событие. Вероятность достоверного события равна единице. Вероятность невозможного события равна нулю.
то это достоверное событие. Вероятность достоверного события равна единице. Вероятность невозможного события равна нулю.
 будет равна
будет равна  , вероятность того, что стрелка прибора выйдет за пределы шкалы (
, вероятность того, что стрелка прибора выйдет за пределы шкалы (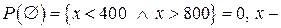 показание прибора). Вероятность невозможного события равна нулю. Вероятность того, что стрелка прибора будет находиться в диапазоне
показание прибора). Вероятность невозможного события равна нулю. Вероятность того, что стрелка прибора будет находиться в диапазоне  (рисунке 1.2) находится между нулем и единицей (
(рисунке 1.2) находится между нулем и единицей (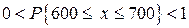 ).
). очень слабо меняется и может служить оценкой вероятности
очень слабо меняется и может служить оценкой вероятности  (1.3)
(1.3) относительная частота случайного события
относительная частота случайного события 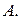
 .
. (1.4)
(1.4) достаточно малое положительное число. Это означает, что разность между относительной частотой
достаточно малое положительное число. Это означает, что разность между относительной частотой 
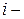 го случайного события и вероятностью
го случайного события и вероятностью 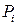 его появления является сколь угодно малой величиной. Это свойство относительных частот, как уже отмечалось ранее, называется статистической устойчивостью частот.
его появления является сколь угодно малой величиной. Это свойство относительных частот, как уже отмечалось ранее, называется статистической устойчивостью частот. и вероятностью
и вероятностью 
 – вероятность случайного события
– вероятность случайного события  является неотрицательным числом.
является неотрицательным числом. – вероятность достоверного события
– вероятность достоверного события  равна единице.
равна единице. – вероятность невозможного события
– вероятность невозможного события  равна нулю.
равна нулю. (1.6)
(1.6) независимые случайные события.
независимые случайные события.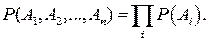 (1.7)
(1.7) являются зависимыми и событие
являются зависимыми и событие  предшествует событию
предшествует событию  (1.8)
(1.8) – условная вероятность.
– условная вероятность. равна единице
равна единице (1.9)
(1.9)


