
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод наименьших квадратов для полиномиальных моделейСодержание книги
Поиск на нашем сайте
порядка Обозначим
Вектор неизвестных параметров
Изменив порядок суммирования, получим уравнение вида:
В конечном виде уравнение можно представить как:
Обозначим как
Транспонированная матрица
В матричной форме система линейных алгебраических уравнений для метода наименьших квадратов будет иметь вид:
отсюда следует, что вектор
Рассмотрим пример линейной регрессионной зависимости:
транспонированная матрица базисных функций. (2.42)
Тогда систему линейных алгебраических уравнений для этого примера можно представить в виде:
(2.43)
,
Решая систему уравнений получим значения коэффи-
2.4. Нормы вектора и матрицы
Нормой · · Для любого вектора ·
Норма является количественной характеристикой вектора Наиболее распространенными нормами являются:
Вторая норма, называемая Евклидовой, используется наиболее часто. Нормой матрицы называется величина
Норма матрицы обладает следующими свойствами: · · Для любой матрицы · · · Существуют следующие нормы матриц:
Здесь
2.5. Обусловленность системы линейных алгебраических уравнений
Рассмотрим систему из двух алгебраических уравнений
Дадим геометрическую интерпретацию решения этой системы уравнений, рисунок 2.2.
Рисунок 2.2. Графическая интерпретация решений систем линейных алгебраических уравнений а – единственное решение,
в – матрица А плохо обусловлена,
В случае а) система уравнений имеет единственное решение. Прямые линии в случае б) идут параллельно, то есть система уравнений несовместна. В случае в) из-за плохой обусловленности матрицы А незначительные изменения вектора правых частей или коэффициентов системы ограничений приводит к резкому изменению решения системы уравнений. Это означает, что определитель матрицы На практике применения метода наименьших квадратов на ЭВМ может оказаться, что определитель матрицы
Определитель матрицы системы уравнений
При увеличении
Матрица Гильберта является плохо обусловленной. Обусловленность матрицы системы алгебраических уравнений определяется числом обусловленности
(2.53)
где Число обусловленности Рассмотрим, как влияет изменение
где частей
Из уравнения (3.4) следует, что
Из определения числа обусловленности
(2.56)
Из этих неравенств можно получить неравенство:
(2.57)
где
-относительное изменение вектора правых частей.
роль множителя, увеличивающего относительную ошибку решения системы уравнений.
(2.58) В частности число обусловленности единичной матрицы Число обусловленности ортогональной матрицы Если
Число обусловленности матрицы Гильберта Пример. Дана система линейных алгебраических уравнений
Точным решением этой системы уравнений будет
Изменив правую часть системы уравнений
Это произошло из-за того, что Плохая обусловленность матрицы Влияние плохой обусловленности значительно уменьшается, если вместо полиномиальной модели
представляющую собой линейную комбинацию элементов подсистемы базисных функций
где Система полиномов
является ортогональной, если выполняется условие
2.6. Применение ортогональных полиномов Чебышева и Форсайта
Ортогональные полиномы Чебышева имеют вид:
где Согласно методу наименьших квадратов
транспонированная матрица базисных функций. (2.69)
Используя уравнение для ортогональных полиномов, получим
(2.71)
Оценки коэффициентов не коррелированы между собой и имеют дисперсии
(2.72)
где Дисперсия
(2.73)
где значения выходной величины, полученные по уравнению регрессии в точках При решении практических задач степень аппроксимирующего полинома обычно неизвестна, поэтому выбор степени полинома осуществляется следующим образом. Аппроксимирующая функция
где Аппроксимирующую функцию можно представить в виде алгебраического полинома
где
Ввод данных (экспериментальная зависимость)
Величина остаточной дисперсии
Процедура вычисления коэффициентов путем преобразования полиномов Чебышева в системе Mathcad
Ввод исходных данных (экспериментальная зависимость)
Ортогональные полиномы Форсайта
Ортогональные полиномы Форсайта имеют вид:
где
Преобразование полиномов Форсайта осуществляется по формулам (4) - (6), аналогично полиномам Чебышева. Здесь
Полиномы Форсайта при преобразовании их в обычные полиномы будут иметь вид:
Процедура вычисления коэффициентов путем преобразования ортогональных полиномов Форсайта в системе Mathcad
Как показывают расчеты, полученные при использовании процедур Использование алгебраических полиномов значительно уменьшает вычислительную погрешность при сохранении всех замечательных свойств полиномов Чебышева и Форсайта (реккурентность и ортогональность). При этом обычные алгебраические полиномы позволяют вычислять любое значение выходной величины
2.7. Регрессионный анализ для многомерных линейных моделей [3]
Пусть задана таблица плана эксперимента с
Таблица 2.1
С использованием метода наименьших квадратов можно найти коэффициенты
где
Представим данные в таблице 1 в матричной форме:
вектор неизвестных коэффициентов регрессионной модели. (2.82)
Транспонированная матрица
Система нормальных уравнений для определения коэффициентов
В матричной форме система уравнений имеет вид:
Перемножив матрицы
Матрица Вектор правых частей в развернутой форме:
Вектор коэффициентов
Обратная матрица
Элементы обратной матрицы представляют собой следующие выражения:
где Вычисление обратной матрицы осуществляется по следующей формуле:
где Чтобы существовала обратная матрица
(2.92)
Это означает, что ни один элемент Пример линейной зависимости двух столбцов:
Здесь второй столбец матрицы является линейной комбинации первого столбца, то есть
(2.93)
Здесь вектор значений функций отклика, вычисленных по уравнению регрессии. Числитель остаточной дисперсии получается умножением матриц
(2.94)
Обозначим через Дисперсии
Коэффициенты Тогда математическое ожидание
где
Таким образом, диагональные элементы матрицы представляют собой дисперсии, необходимые для проверки значимости коэффициентов регрессии, а недиагональные элементы - ковариации соответствующих коэффициентов регрессии, которые определяют статистическую зависимость между коэффициентами. Выразим матрицу В результате получим уравнение:
где
Примечание. Ковариация между элементами
Матрица коэффициентов системы нормальных уравнений является симметричной и поэтому
Полагая
Таким образом, имеем зависимость:
Отсюда получаем следующие зависимости:
Матрица
можно рассматривать только как средство ранжирования факторов по степени влияния на выходную величину.
2.8. Аппроксимация экспериментальных зависимостей кубическими сплайнами [23] Кубические сплайн-функции предназначены для интерполяции сложных кривых. Сплайн моделирует старое механическое устройство, которое использовалось чертежниками для построения гладких кривых. Механический сплайн, изготовленный из упругого материала, закрепляли, подвешивая грузила в заданных точках (узлах интерполяции). Сплайн принимает форму, которая минимизирует потенциальную энергию. Эта энергия пропорциональна интегралу по длине дуги от квадрата кривизны сплайна.
Рисунок 2.3. Сплайн
Вторая производная
. (2.105)
Сплайн-функция Если на границах всего диапазона [ Иногда вместо естественных граничных условий используются некоторые другие условия вблизи и на границах табличной зависимости. На рисунке 2.4 показана графическая иллюстрация интерполяции табличной функции кубическими сплайнами.
Рисунок 2.4. Графическая иллюстрация интерполяции кубическими сплайнами
Рассмотрим построение кубического сплайна в подинтервал
Из соотношения следует, что:
В результате интегрирования выражения получим выражение кубического сплайна вида:
Функция Первая производная от функции сплайна
Коэффициенты сплайна Как уже отмечалось выше, левосторонняя и правосторонняя производные на стыке двух сплайнов
должны быть равны, поэтому можно записать следующее уравнение:
где
Из уравнения можно получить систему линейных алгебраических уравнений вида:
где
Для того, чтобы решить систему уравнений, необходимо добавить еще два уравнения, граничные условия. Для естественного кубического сплайна должны выполняться граничные условия вида:
Коэффициенты сплайна
(2.115)
Значения
Система уравнений имеет решение, поскольку в ее матрице диагональные элементы доминируют (преобладают) над элементами, не лежащими на главной диагонали, то есть Пример. В статье [20] приведена зависимость адсорбции поливинилового спирта
Таблица 2.2
Вычисление кубического сплайна в системе Mathcad
Ввод исходных данных
Ниже приведены графики экспериментальной и интерполирующей зависимостей с применением встроенных функций Spline и Interp.
Здесь точками обозначена экспериментальная зависимость Глава 3 Планирование многофакторных экспериментов Факторы Фактором называется измеряемая величина, принимающая в некоторый момент времени определенное значение. Факторы соответствуют способам воздействия на объект исследования. После того как выбран объект исследования и выходная величина, нужно включить в рассмотрение все наиболее существенные факторы, которые могут влиять на процесс (объект). Если к
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 1844; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.92.87 (0.015 с.) |

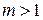
 алгебраический полином
алгебраический полином  й степени как:
й степени как: (2.29)
(2.29) имеет вид:
имеет вид: (2.30)
(2.30) (2.31)
(2.31) (2.32)
(2.32) (2.33)
(2.33) (2.34)
(2.34) . (2.35)
. (2.35)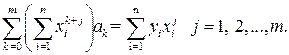 (2.36)
(2.36) матрицу базисных функций
матрицу базисных функций (2.37)
(2.37) базисных функций:
базисных функций: (2.38)
(2.38) (2.39)
(2.39) (2.40)
(2.40)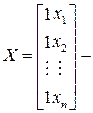 матрица базисных функций. (2.41)
матрица базисных функций. (2.41)

 (2.44)
(2.44) циентов
циентов  и
и  линейного регрессионного уравнения
линейного регрессионного уравнения вектора
вектора  Норма
Норма 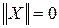 только в случае
только в случае 
 выполняется условие
выполняется условие  .
. неравенство треугольника.
неравенство треугольника.

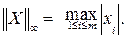 (2.45)
(2.45) (2.46)
(2.46) Норма
Норма  только в случае
только в случае 
 .
. для любых матриц
для любых матриц  .
. для любых матриц
для любых матриц  для любой матрицы
для любой матрицы 

 (2.47)
(2.47) собственные числа матрицы
собственные числа матрицы  Собственные числа и их вычисление будут рассмотрены ниже.
Собственные числа и их вычисление будут рассмотрены ниже.


 (2.48)
(2.48)
 ; б – нет решения,
; б – нет решения,  ;
;
 близок к нулю, а матрица
близок к нулю, а матрица  [23]. Особенно неблагоприятная ситуация возникает в случае, когда точки
[23]. Особенно неблагоприятная ситуация возникает в случае, когда точки 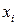 равномерно расположены на отрезке
равномерно расположены на отрезке  . Без потери общности можно предположить, что
. Без потери общности можно предположить, что  Тогда элементы матрицы системы нормальных уравнений
Тогда элементы матрицы системы нормальных уравнений 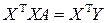 имеют вид:
имеют вид: (2.49)
(2.49) (2.50)
(2.50)
 где определитель матрицы Гильберта порядка.
где определитель матрицы Гильберта порядка. матрица Гильберта. (2.51)
матрица Гильберта. (2.51)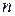 определитель Гильберта очень быстро стремится к нулю. Определитель Гильберта вычисляется по формуле:
определитель Гильберта очень быстро стремится к нулю. Определитель Гильберта вычисляется по формуле: (2.52)
(2.52)


 нормы вектора и матрицы соответственно.
нормы вектора и матрицы соответственно. Чем больше число обусловленности
Чем больше число обусловленности  тем матрица
тем матрица  ближе к вырожденной (
ближе к вырожденной (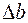 правой части
правой части  системы уравнений
системы уравнений  на решение
на решение  . Для этого представим систему уравнений в виде
. Для этого представим систему уравнений в виде (2.54)
(2.54) – изменение вектора решения при изменении вектора правых
– изменение вектора решения при изменении вектора правых (2.55)
(2.55) (3.3) следует, что
(3.3) следует, что

 – относительное изменение вектора решения;
– относительное изменение вектора решения;
 Неравенство (2.57) показывает, что относительное изменение вектора правых частей увеличивает относительную ошибку решения
Неравенство (2.57) показывает, что относительное изменение вектора правых частей увеличивает относительную ошибку решения на величину
на величину  То же самое верно и в отношении изменений в коэффициентах матрицы
То же самое верно и в отношении изменений в коэффициентах матрицы 
 .
. (
( ) также равно единице.
) также равно единице. диагональная матрица, то число обусловленности
диагональная матрица, то число обусловленности (2.59)
(2.59) является величиной порядка
является величиной порядка 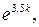 где
где  размерность матрицы. Определитель матрицы
размерность матрицы. Определитель матрицы  , обратной к матрице
, обратной к матрице  Поэтому обратная матрица
Поэтому обратная матрица 
 (2.60)
(2.60) (2.61)
(2.61)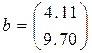 , получим следующее решение:
, получим следующее решение: (2.62)
(2.62)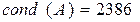 , то есть матрица
, то есть матрица  приводит к тому, что появление даже самых малых ошибок в правой части системы нормальных уравнений вызывает появление больших ошибок в решении системы. Уже при
приводит к тому, что появление даже самых малых ошибок в правой части системы нормальных уравнений вызывает появление больших ошибок в решении системы. Уже при  в расчетах на ЭВМ, оперирующих восьмизначными цифрами, получаются совершенно неверные результаты, что видно из приведенного выше примера. Например, при
в расчетах на ЭВМ, оперирующих восьмизначными цифрами, получаются совершенно неверные результаты, что видно из приведенного выше примера. Например, при 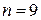 матрица
матрица  обратная к матрице Гильберта
обратная к матрице Гильберта  содержит элементы порядка
содержит элементы порядка  Поэтому даже ошибка порядка
Поэтому даже ошибка порядка  в правых частях и коэффициентах системы нормальных уравнений может привести к ошибке порядка 3 в решении системы.
в правых частях и коэффициентах системы нормальных уравнений может привести к ошибке порядка 3 в решении системы.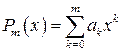 используется модель вида
используется модель вида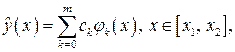 (2.63)
(2.63) , (2.64)
, (2.64)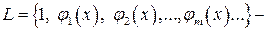 ортогональные полиномы.
ортогональные полиномы. (2.65)
(2.65) (2.66)
(2.66)



 матрицы
матрицы  будут иметь вид:
будут иметь вид: матрица базисных функций. (2.68)
матрица базисных функций. (2.68)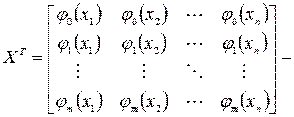
 (2.70)
(2.70)
 Из линейной алгебры известно, что матрица, обратная к диагональной, также является диагональной, причем ее элементы равны обратным величинам диагональных элементов исходной матрицы. Поэтому, учитывая, что решение нормальной системы уравнений по формуле
Из линейной алгебры известно, что матрица, обратная к диагональной, также является диагональной, причем ее элементы равны обратным величинам диагональных элементов исходной матрицы. Поэтому, учитывая, что решение нормальной системы уравнений по формуле  получим оценки коэффициентов модели
получим оценки коэффициентов модели

 дисперсия случайных ошибок эксперимента.
дисперсия случайных ошибок эксперимента. , как правило, неизвестна, поэтому можно использовать ее оценку
, как правило, неизвестна, поэтому можно использовать ее оценку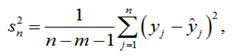

 Если модель выбрана правильно, то оценка дисперсии
Если модель выбрана правильно, то оценка дисперсии 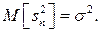
 имеет вид
имеет вид (2.74)
(2.74) - коэффициенты многочлена.
- коэффициенты многочлена. (2.75)
(2.75)


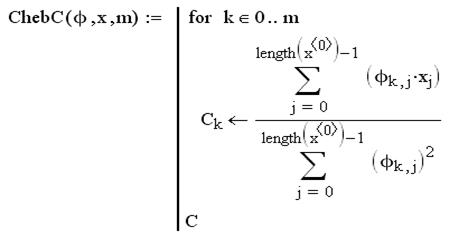


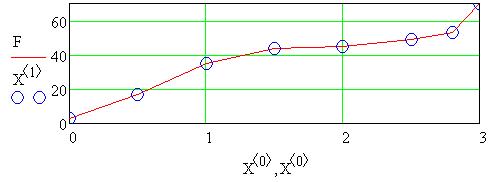
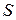 указывает на хорошее совпадение аппроксимирующей и табличной зависимостей.
указывает на хорошее совпадение аппроксимирующей и табличной зависимостей.
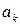 алгебраического полинома
алгебраического полинома





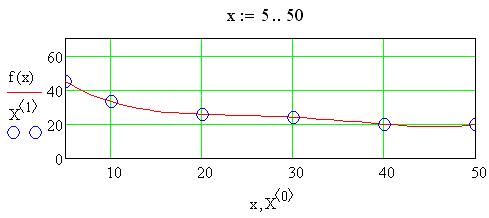

 (2.76)
(2.76)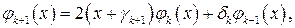
 (2.77)
(2.77)
 (2.79)
(2.79)

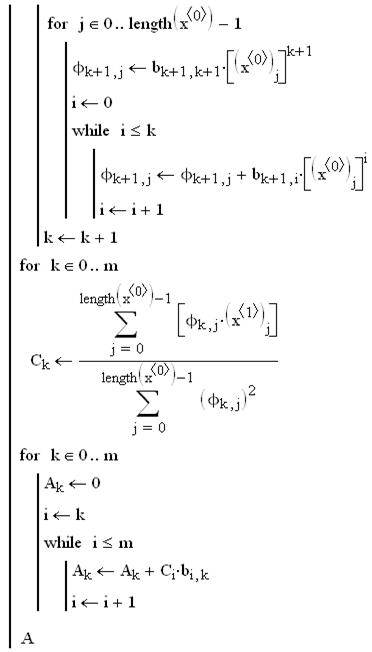



 , налицо полное совпадение значений выходной величины, полученных по результатам эксперимента, и по аппроксимирующей функции
, налицо полное совпадение значений выходной величины, полученных по результатам эксперимента, и по аппроксимирующей функции  . Величина остаточной дисперсии
. Величина остаточной дисперсии  в исследуемом диапазоне аргумента
в исследуемом диапазоне аргумента  . Кроме того, алгебраические полиномы легко вычислять, дифференцировать и интегрировать.
. Кроме того, алгебраические полиномы легко вычислять, дифференцировать и интегрировать.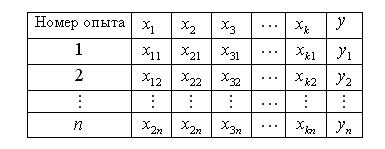
 уравнения регрессии по данным таблицы 1:
уравнения регрессии по данным таблицы 1:
 фиктивная переменная, равная единице.
фиктивная переменная, равная единице.
 вектор наблюдений. (2.81)
вектор наблюдений. (2.81)
 (2.83)
(2.83) (2.84)
(2.84) (2.85)
(2.85) (2.86)
(2.86) называется матрицей моментов.
называется матрицей моментов. (2.87)
(2.87)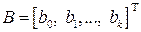 определяется из уравнения:
определяется из уравнения: (2.88)
(2.88) может быть представлена в виде:
может быть представлена в виде: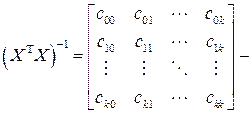 ковариационная матрица. (2.89)
ковариационная матрица. (2.89) (2.90)
(2.90)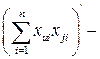 алгебраическое дополнение элемента
алгебраическое дополнение элемента 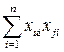 в матрице
в матрице 
 (2.91)
(2.91) определитель матрицы, полученной после вычеркивания
определитель матрицы, полученной после вычеркивания 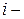 строки и
строки и 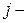 го столбца матрицы
го столбца матрицы 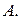 На пересечении
На пересечении  матрицы
матрицы 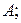
 определитель матрицы
определитель матрицы 
 были линейно независимы, то есть должны выполняться условия
были линейно независимы, то есть должны выполняться условия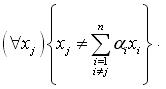
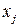 не является линейной комбинацией других элементов
не является линейной комбинацией других элементов  В этом случае в матрице независимых переменных элементы одного столбца не будут линейной комбинацией соответствующих элементов других столбцов.
В этом случае в матрице независимых переменных элементы одного столбца не будут линейной комбинацией соответствующих элементов других столбцов. .
.
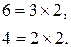
 Для вычисления остаточной дисперсии вычисляют значения элементов вектора
Для вычисления остаточной дисперсии вычисляют значения элементов вектора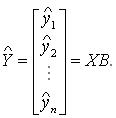


 вектор-столбец коэффициентов истинной регрессии, при этом математическое ожидание вектора оценок коэффициентов регрессии
вектор-столбец коэффициентов истинной регрессии, при этом математическое ожидание вектора оценок коэффициентов регрессии  Оценки коэффициентов
Оценки коэффициентов 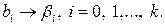
 коэффициентов регрессии определяются по формуле:
коэффициентов регрессии определяются по формуле: (2.95)
(2.95) являются элементами ковариационной матрицы, стоящими на главной диагонали.
являются элементами ковариационной матрицы, стоящими на главной диагонали. определяется выражением:
определяется выражением:
 (2.96)
(2.96)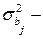 генеральная дисперсия
генеральная дисперсия 
 ковариационный момент между коэффициентами
ковариационный момент между коэффициентами  и
и 
 (2.97)
(2.97) случайный нормальный вектор с независимыми элементами, имеющими дисперсии
случайный нормальный вектор с независимыми элементами, имеющими дисперсии 
 (2.98)
(2.98)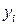 векторов
векторов  определяется следующим соотношением:
определяется следующим соотношением: (2.99)
(2.99) (2.100)
(2.100) и, учитывая статистическую независимость, получим:
и, учитывая статистическую независимость, получим: (2.101)
(2.101) (2.102)
(2.102) (2.103)
(2.103) (2.104)
(2.104)
 (
(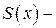 сплайн - функция) примерно равна кривизне. Это означает, что кривизна такого сплайна пропорциональна интегралу
сплайн - функция) примерно равна кривизне. Это означает, что кривизна такого сплайна пропорциональна интегралу
 , для которой
, для которой  интеграл (2.105) имеет минимальное значение. Эта функция является полиномом третьей степени. Каждый отрезок между двумя соседними узлами интерполяции описывается своей сплайн – функцией
интеграл (2.105) имеет минимальное значение. Эта функция является полиномом третьей степени. Каждый отрезок между двумя соседними узлами интерполяции описывается своей сплайн – функцией 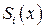 . Соседние полиномы соединяются непрерывно.
. Соседние полиномы соединяются непрерывно. ]
]  , то такой сплайн называется естественным кубическим сплайном. С математической точки зрения естественный кубический сплайн является самой гладкой функцией, интерполирующей заданные точки.
, то такой сплайн называется естественным кубическим сплайном. С математической точки зрения естественный кубический сплайн является самой гладкой функцией, интерполирующей заданные точки.

 Обозначим вторую производную от
Обозначим вторую производную от  как
как  Поскольку на каждом отрезке кубический сплайн совпадает с кубическим полиномом, то
Поскольку на каждом отрезке кубический сплайн совпадает с кубическим полиномом, то 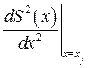 должна быть линейной функцией. Это означает, что график линейной функции проходит через точки
должна быть линейной функцией. Это означает, что график линейной функции проходит через точки  . В этом случае эту функцию можно представить в виде:
. В этом случае эту функцию можно представить в виде: (2.106)
(2.106) (2.107)
(2.107)
 (2.108)
(2.108)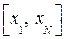 левосторонняя и правосторонняя производные равны между собой.
левосторонняя и правосторонняя производные равны между собой.
 (2.109)
(2.109) являются неизвестными, поскольку неизвестна вторая производная
являются неизвестными, поскольку неизвестна вторая производная 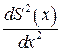 функции
функции 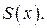
 (2.110)
(2.110) (2.111)
(2.111) (2.112)
(2.112)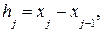
 .
.

 (2.114)
(2.114)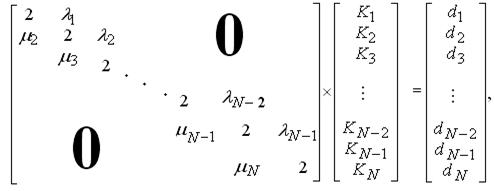
 вычисляются по формулам:
вычисляются по формулам:
 (2.116)
(2.116) (2.117)
(2.117)
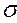 от концентрации его раствора
от концентрации его раствора  , полученная по результатам эксперимента при производстве декоративно-защитных материалов на бумажной основе таблица 2.2.
, полученная по результатам эксперимента при производстве декоративно-защитных материалов на бумажной основе таблица 2.2.


 , сплошной линией – интерполирующая зависимость. Как видно из графиков экспериментальная и интерполирующая зависимости полностью совпадают.
, сплошной линией – интерполирующая зависимость. Как видно из графиков экспериментальная и интерполирующая зависимости полностью совпадают.


