
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределения качественных и количественных признаковСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Множество, подлежащих статистическому анализу однородных объектов, называется статистической совокупностью. Отдельные объекты статистической совокупности называются ее элементами. Например, в качестве статистической совокупности можно взять множество однотипных станков, каждый из которых характеризуется своей производительностью. Элементами этой совокупности являются станки. Количество станков в совокупности ее объемом [24]. Отдельные элементы совокупности могут быть охарактеризованы одним или несколькими признаками. Значения признаков для отдельных элементов совокупности могут варьироваться. Признак называется атрибутивным, если является качественным, или количественным – если отдельные значения вариантов выражаются числами (например, объем, масса и т. д.). Некоторые признаки можно упорядочить по номерам, которые называются рангами. Использование ранговой шкалы позволяет проводить статистический анализ данных при помощи непараметрических методов. Количественные признаки могут быть дискретными (отдельные числа) и непрерывными (изменяющиеся в некотором числовом диапазоне). Изучение изменения значений (вариантов) признака проводится статистическое наблюдение (измерение, регистрация, описание и т. д.). В результате наблюдения определяются значения (варианты) признака, которые соответствуют каждому элементу совокупности. Статистические наблюдения могут быть сплошными, при которых изучается каждый элемент совокупности, или выборочными – изучается только некоторое ограниченное число элементов (выборка). Изучаться может один или несколько признаков. Если элементы совокупности можно охарактеризовать одним качественным признаком, который имеет только два возможных значения: «признак есть
Относительные частоты или доли признака:
Вариация признака может иметь не два, а более вариантов, то есть
Таблица 1.4
Для оценки взаимозависимости между двумя признаками использовать таблицы сопряженности. При этом число возможных значений каждого признака должно быть зафиксировано. Пусть число значений признака
Чтобы установить, есть ли зависимость между признаками, необходимо воспользоваться критерием Пирсона. Для этого необходимо вычислить расчетный коэффициент
Расчетный коэффициент Пирсона Пример. Пусть имеется три станка, разлчиающихся друг от друга степенью износа (признак А). На каждом из них обрабатываются одинаковые детали. Известен примерный процент бракованных деталей может находиться в диапазоне от 5 до 7 для каждого станка (признак В). Всего прошли обработку на всех станках 120 деталей. Данные наблюдений сведены в таблицу 1.6.
Необходимо проверить гипотезу о взаимосвязи процента бракованных деталей от степени износа станков по критерию Пирсона. Вычислим расчетный коэффициент
Для q=5% и числе степеней свободы f=(3
1.25.2. Распределение количественных признаков [24]
Пусть получена выборка наблюдений Для удобства анализа данных, их группируют по отдельным признакам. Каждая группа данных соответствуют своему признаку
Таблица 1.7
Если разделить каждую частоту Накопленная (кумулятивная) частота – это частота, которая равна количеству элементов статистической совокупности с признаком
(1.92)
Выражение в формуле (1.94) означает, что
Таблица 1.8
График кумулятивного вариационного ряда представляет собой ступенчатую разрывную в точках
Рисунок 1.22. Кумулята дискретного распределения
Когда количество различных вариант достаточно велико, необходимо использовать интервальную группировку данных. В этом случае весь диапазон от
Таблица 1.9
При использовании интервалов различной длины
которая равна числу элементов, приходящееся на единицу длины.
1.25.3. Ранговая корреляция [24] Чтобы установить наличие или отсутствия взаимосвязи между двумя качественными признаками
· по признаку · по признаку
Коэффициент ранговой корреляции Спирмена вычисляется по формуле:
где
Коэффициент
Абсолютная величина Проверка значимости коэффициента Пример. Пусть необходимо узнать существует ли зависимость между сложностью схем раскроя плитных древесных материалов (признак
Рисунок 1.23. Виды схем раскроя
В таблице 1.10 приведены результаты ранжирования схем раскроя в зависимости от их сложности и диапазонов возможного полезного выхода по каждой схеме. Таблица 1.10
Вычисляем коэффициент ранговой корреляции
Затем вычисляем расчетный коэффициент Стьюдента 1.25.4. Коэффициент конкордации [24] Коэффициент конкордации может быть использован, например, для согласования мнений экспертов при ранжировании произвольного числа признаков · · · · · · Необходимо выявить наиболее важные из выбранных факторов, чтобы затем провести с ними дальнейшие исследования. Эксперты (технологи, экономисты, менеджеры и другие специалисты) должны дать свою оценку каждому из предложенных факторов, то есть ранжировать факторы по степени их влияния на исследуемую систему. Данные опроса экспертов можно представить в виде таблицы 1.11. Таблица 1.11
Здесь Чтобы решить вопрос о степени согласованности мнений экспертов необходимо использовать, так называемым, коэффициентом конкордации. Этот коэффициент можно вычислить по формуле:
Коэффициент конкордации может находиться в пределах
Полученное значение
где Пример. Пусть исследуется зависимость полезного выхода заготовок от следующих организационно-технологических факторов раскроя плитных древесных материалов: 1. 2. 3. 4. 5. 6. 7. 8. раскроя; 9. В таблице 1.12 приведены данные опроса экспертов.
Таблица 1.12
Используя систему Mathcad вычислим значение коэффициента конкордации W.
Далее мы проверим значимость коэффициента конкордации W который будет равен Глава 2 Метод наименьших квадратов
|
|||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 732; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.166.224 (0.011 с.) |

 » или «признака нет
» или «признака нет  ». Например, измеряется признак тапа «брак» в некоторой партии изделий. В таблице 1.2 представлены результаты наблюдений.
». Например, измеряется признак тапа «брак» в некоторой партии изделий. В таблице 1.2 представлены результаты наблюдений.

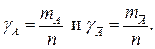
 . Если провести многоразрядную (множественную) группировку, получим распределение, представленное в таблице 1.4.
. Если провести многоразрядную (множественную) группировку, получим распределение, представленное в таблице 1.4.
 и
и  можно
можно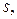 а признака
а признака 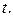 В таблице 1.5. приведены количества наблюдений
В таблице 1.5. приведены количества наблюдений  в которых признак
в которых признак 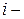 е значение, а признак
е значение, а признак 
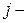 е значение [1].
е значение [1].
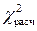
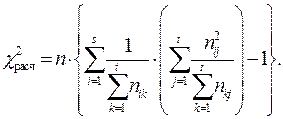 (1.91)
(1.91) при выбранном уровне значимости q и числе степеней свободы f=(s
при выбранном уровне значимости q и числе степеней свободы f=(s  1)(t
1)(t 
 .
. Поскольку
Поскольку 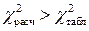 можно сделать вывод о том, что существует взаимосвязь между степенью износа станков и процентом бракованных деталей.
можно сделать вывод о том, что существует взаимосвязь между степенью износа станков и процентом бракованных деталей. (
( ) для изучения вариации некоторого признака
) для изучения вариации некоторого признака  . Среди сделанных наблюдений
. Среди сделанных наблюдений 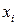 . Количество элементов в
. Количество элементов в  называется частотой варианты
называется частотой варианты  Если сопоставить каждой варианте
Если сопоставить каждой варианте 
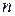 , получим распределение относительных частот
, получим распределение относительных частот 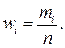 Для относительных частот выполняется условие
Для относительных частот выполняется условие 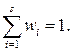
 Относительная накопленная частота
Относительная накопленная частота 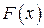 определяется следующим образом:
определяется следующим образом:
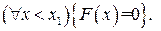 То есть, для любого
То есть, для любого 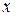 нет элементов, меньше чем
нет элементов, меньше чем 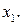 Для значений
Для значений 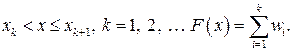 Таким образом, относительная частота
Таким образом, относительная частота 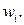 Кумулятивный вариационный ряд строится в виде таблицы 1.8.
Кумулятивный вариационный ряд строится в виде таблицы 1.8.
 кривую, рисунок 1.22.
кривую, рисунок 1.22.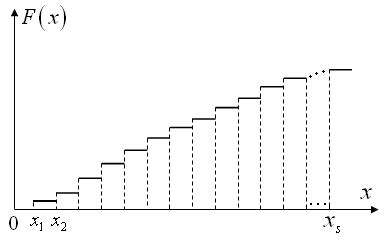
 (минимальное значения) до
(минимальное значения) до 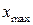 (максимальное значения) разбивается на отдельные равные или неравные интервалы
(максимальное значения) разбивается на отдельные равные или неравные интервалы  Каждый интервал имеет свой признак. Через
Каждый интервал имеет свой признак. Через  обозначены численности групп данных. В результате такой группировки получается интервальный вариационной ряд или интервальное распределение, представленный в таблице 1.9. Здесь
обозначены численности групп данных. В результате такой группировки получается интервальный вариационной ряд или интервальное распределение, представленный в таблице 1.9. Здесь  относительные частоты,
относительные частоты, 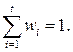

 , было введено понятие плотности частоты
, было введено понятие плотности частоты (1.93)
(1.93)
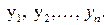
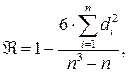 (1.94)
(1.94)
 также, как коэффициент корреляции, изменяется в пределах
также, как коэффициент корреляции, изменяется в пределах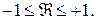 (1.95)
(1.95)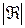 увеличивается с увеличением степени зависимости между признаками
увеличивается с увеличением степени зависимости между признаками 

 .
.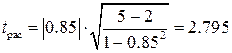 . По таблице значений коэффициента Стьюдента при уровне значимости q=5% и числе степеней свободы f=5-3 находим
. По таблице значений коэффициента Стьюдента при уровне значимости q=5% и числе степеней свободы f=5-3 находим 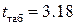 . Поскольку
. Поскольку 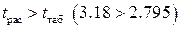 , можно считать, что связь между сложностью схем раскроя и полезным выходом заготовок установлена.
, можно считать, что связь между сложностью схем раскроя и полезным выходом заготовок установлена.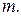 Например, при планировании производства изделий мебельной фабрики необходимо учитывать множество факторов, как производства, так и реализации готовой продукции. Возьмем для примера лишь некоторые из них. Нами выбраны следующие факторы:
Например, при планировании производства изделий мебельной фабрики необходимо учитывать множество факторов, как производства, так и реализации готовой продукции. Возьмем для примера лишь некоторые из них. Нами выбраны следующие факторы: процент загрузки производственных мощностей предприятия;
процент загрузки производственных мощностей предприятия; обеспеченность производства необходимыми ресурсами (сырье, материалы, комплектующие, энерго- и теплоснабжение, трудовые ресурсы и т. д.);
обеспеченность производства необходимыми ресурсами (сырье, материалы, комплектующие, энерго- и теплоснабжение, трудовые ресурсы и т. д.);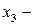 уровень качества выпускаемой продукции в зависимости от состояния оборудования предприятия (соответствие мировому уровню, степенью износа и т. д.);
уровень качества выпускаемой продукции в зависимости от состояния оборудования предприятия (соответствие мировому уровню, степенью износа и т. д.);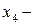 удаленность предприятия от торговых центров, которые, как правило, находятся в больших городах (большие транспортные расходы);
удаленность предприятия от торговых центров, которые, как правило, находятся в больших городах (большие транспортные расходы);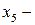 возможности потенциальных потребителей продукции предприятия;
возможности потенциальных потребителей продукции предприятия; затраты на рекламу (объявления в газетах, центральных или местных, реклама на радио или по телевидению, по центральному или местному и т. п.).
затраты на рекламу (объявления в газетах, центральных или местных, реклама на радио или по телевидению, по центральному или местному и т. п.).
 ранг, присвоенный
ранг, присвоенный  (1.96)
(1.96) Чем больше величина
Чем больше величина  , тем больше согласованность мнений экспертов. Значимость коэффициента конкордации проверяется по
, тем больше согласованность мнений экспертов. Значимость коэффициента конкордации проверяется по 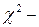 критерию Пирсона (при
критерию Пирсона (при 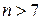 ). Расчетный коэффициент
). Расчетный коэффициент  вычисляется по формуле:
вычисляется по формуле: (1.97)
(1.97)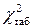 при уровне значимости q и числе степеней свободы f = n – 1. Если выполняется неравенство
при уровне значимости q и числе степеней свободы f = n – 1. Если выполняется неравенство  , то можно принять гипотезу о согласованности мнений экспертов при данном уровне значимости. В том случае, когда эксперт считает, что некоторые факторы имеют одинаковое влияние на исследуемую систему, он присваивает этим факторам один и тот же, так называемый, связанный ранг. ранг. Связанный рангвычисляется как среднее мест, которые эксперты присвоили этим факторам. Например, пусть три фактора находятся на 2, 4 и 6 местах, тогда связанный ранг будет равен (2+4+6)/3=4. Этот ранг и будет присвоен каждому из этих факторов. Если в оценках экспертов имеются связанные ранги, то формула для вычисления коэффициента конкордации будет иметь вид
, то можно принять гипотезу о согласованности мнений экспертов при данном уровне значимости. В том случае, когда эксперт считает, что некоторые факторы имеют одинаковое влияние на исследуемую систему, он присваивает этим факторам один и тот же, так называемый, связанный ранг. ранг. Связанный рангвычисляется как среднее мест, которые эксперты присвоили этим факторам. Например, пусть три фактора находятся на 2, 4 и 6 местах, тогда связанный ранг будет равен (2+4+6)/3=4. Этот ранг и будет присвоен каждому из этих факторов. Если в оценках экспертов имеются связанные ранги, то формула для вычисления коэффициента конкордации будет иметь вид (1.98)
(1.98)
 количество типов связанных рангов у
количество типов связанных рангов у  го эксперта;
го эксперта;  количество экспертов, использовавшее связанные ранги.
количество экспертов, использовавшее связанные ранги. наличие автоматических разгрузочных устройств;
наличие автоматических разгрузочных устройств; ручная выгрузка и штабелирование заготовок после
ручная выгрузка и штабелирование заготовок после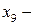 тип станка (с программным управлением, полуавтомат).
тип станка (с программным управлением, полуавтомат).

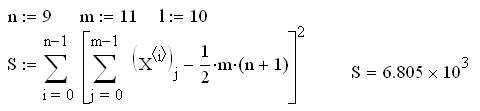

 При уровне значимости q=5% и числе свободы f = 9
При уровне значимости q=5% и числе свободы f = 9 


