
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сущность метода наименьших квадратов
Уравнение приближенной регрессии существенно зависит от выбранного метода приближения. Пусть задан некоторый класс функций
Критерием приближения в методе наименьших квадратов является функция:
Здесь Решение задачи аппроксимации табличной экспериментальной зависимости
(2.3)
при которых критерий оптимизации Таким образом, критерий оптимизации
Необходимым и достаточным условием минимума функции
Частные производные
После преобразования уравнения будут иметь вид:
Это система нормальных уравнений. Поскольку выполняется условие При изучении зависимости от одной переменной
Рисунок 2.1. Эмпирическая кривая регрессии
Здесь
Полученные точки последовательно соединяют отрезками прямой. Такая ломаная линия называется эмпирической линией регрессии
Линейная регрессия Пусть необходимо определить коэффициенты
по выборке объема
(2.11)
Система нормальных уравнений при этом будет иметь вид:
В матричной форме данная система имеет вид:
(2.14)
Решение данной системы уравнений может быть представлено, как
(2.15)
Из уравнения
получается, что коэффициент
Это уравнение показывает, что между
После того, как уравнение регрессии найдено, необходимо провести статистический анализ результатов. Этот результата заключается в проверке значимости коэффициентов регрессии и адекватности уравнения. Такое исследование называется регрессионным анализом. При этом принимаются следующие допущения: 1. Фактор 2. Значения 3. Выборочные дисперсии с опытами, которые повторены Оценка значимости коэффициентов
Величина
Если выборочные дисперсии
Незначимые коэффициенты исключаются из уравнения регрессии. Остальные коэффициенты необходимо пересчитать заново, поскольку они коррелированны друг с другом. Адекватность модели (уравнения) проверяется по критерию Фишера:
Сумма квадратов адекватности
Здесь
Сумма квадратов, связанная с дисперсией воспроизводимости:
Дисперсия воспроизводимости
или
Остаточная сумма квадратов
(2.27)
или
(2.28)
Если
|
||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 264; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.76.0 (0.022 с.) |
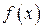 (базисных функций). Например, в качестве базисных функций могут использоваться степенные функции:
(базисных функций). Например, в качестве базисных функций могут использоваться степенные функции: (2.1)
(2.1)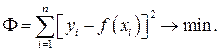 (2.2)
(2.2)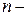 объем выборки;
объем выборки;  экспериментальное значение выходной величины в
экспериментальное значение выходной величины в 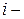 ом опыте;
ом опыте;  значение аппроксимирующей функции в
значение аппроксимирующей функции в  по выше приведенному критерию метода наименьших квадратов сводится к поиску таких значений параметров
по выше приведенному критерию метода наименьших квадратов сводится к поиску таких значений параметров  аппроксимирующей функции
аппроксимирующей функции
 будет принимать минимальное значение.
будет принимать минимальное значение. (2.4)
(2.4)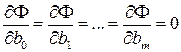 . (2.5)
. (2.5)
 будут иметь вид:
будут иметь вид: (2.6)
(2.6) (2.7)
(2.7)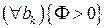 , должен существовать хотя бы один минимум функции
, должен существовать хотя бы один минимум функции  полезно для выбора вида уравнения регрессии построить эмпирическую кривую регрессии, рисунок 2.1. Для этого весь диапазон изменения
полезно для выбора вида уравнения регрессии построить эмпирическую кривую регрессии, рисунок 2.1. Для этого весь диапазон изменения 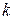 интервалов
интервалов  . Все точки, попавшие в интервал
. Все точки, попавшие в интервал  , относят к его середине. Тогда подсчитываются частные средние
, относят к его середине. Тогда подсчитываются частные средние  для каждого интервала, то есть
для каждого интервала, то есть (2.8)
(2.8)
 число точек в
число точек в  ом интервале;
ом интервале;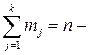 объем выборки. (2.9)
объем выборки. (2.9) от
от  По виду эмпирической зависимости можно подобрать уравнение регрессии
По виду эмпирической зависимости можно подобрать уравнение регрессии и
и  для линейной регрессии по методу наименьших квадратов:
для линейной регрессии по методу наименьших квадратов: (2.10)
(2.10) Критерий оптимизации
Критерий оптимизации 
 (2.13)
(2.13)


 (2.16)
(2.16) (2.17)
(2.17) , который оценивается по формуле:
, который оценивается по формуле: (2.18)
(2.18) Большая ошибка
Большая ошибка  независимые нормально распределенные случайные величины.
независимые нормально распределенные случайные величины. (
( ) раз, однородны. Однородность дисперсий проверяется по критериям Кохрена или Бартлетта.
) раз, однородны. Однородность дисперсий проверяется по критериям Кохрена или Бартлетта. производится по критерию Стьюдента. Для этого вычисляется оценка дисперсии
производится по критерию Стьюдента. Для этого вычисляется оценка дисперсии  коэффициента регрессии
коэффициента регрессии  по формуле:
по формуле: (2.19)
(2.19) определяется по закону накопления ошибок вида:
определяется по закону накопления ошибок вида: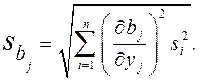 (2.20)
(2.20) однородны, то
однородны, то (2.21)
(2.21) (2.22)
(2.22) Число степеней свободы дисперсии адекватности
Число степеней свободы дисперсии адекватности (2.23)
(2.23) число степеней свободы, связанное с остаточной дисперсией;
число степеней свободы, связанное с остаточной дисперсией; число степеней свободы, связанное с дисперсией воспроизводимости;
число степеней свободы, связанное с дисперсией воспроизводимости; количество коэффициентов в уравнении регрессии.
количество коэффициентов в уравнении регрессии. (2.24)
(2.24) вычисляется по формуле:
вычисляется по формуле: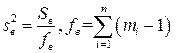 (2.25)
(2.25) (2.26)
(2.26) вычисляется по формуле:
вычисляется по формуле:

 то уравнение регрессии можно считать адекватным моделируемому объекту.
то уравнение регрессии можно считать адекватным моделируемому объекту.


