
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка адекватности регрессионной математической моделиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Использование регрессионной модели позволяет вычислять значения в любой области варьирования факторов. Для чего в уравнение регрессии надо подставить соответствующие значения варьируемых факторов. Проверка адекватности модели необходима для того, чтобы убедиться в том, действительно ли, она правильно отражает поведение исследуемого объекта. Если выходная величина, рассчитанная по модели, существенно не отличается от той, которая получена экспериментальным путем, можно считать, что модель является адекватной. Пусть Если число основных опытов Последовательность действий при проверке математической модели. 1. Рассчитывают сумму квадратов разностей между измеренными а) в случае равномерного дублирования опытов
(3.26)
б) в случае неравномерного дублирования опытов
(3.27)
в) при отсутствии дублирования опытов
(3.28)
· Вычисляют число степеней свободы
2. Вычисляют дисперсию адекватности
3. По критерию Фишера проверяют однородность дисперсий адекватности
Полученное значение Можно оценить эффективность модели (ее информационную ценность). Для этого необходимо сделать следующее. · Вычислить дисперсию относительно среднего значения отклика
где
· Рассчитывают остаточную дисперсию
(3.33)
· Вычисляют величину
Величина
(3.25)
где
Пример обработки результатов полного факторного эксперимента с двумя факторами. План полного факторного плана с двумя факторами представлен в таблице 3.4. Таблице 3.4
Вычисляем средние значения факторов по сериям дублированных опытов:
Поместим данные в таблицу 3.5.
Таблица 3.5
Вычисляем коэффициенты регрессионной математической модели:
Регрессионная математическая модель будет иметь вид:
Вычисление предсказанных значений функции отклика для всех основных опытов:
Проверка однородности дисперсий
Вычисление расчетного коэффициента Кохрена
Табличный коэффициент Кохрена Поскольку Вычисляем дисперсию воспроизводимости
Вычисляем дисперсии коэффициентов регрессии:
Проверяем значимость коэффициентов регрессионной математической модели:
Поскольку Проверка адекватности математической модели осуществляется в следующей последовательности:
· Вычисляется
· Число оцениваемых коэффициентов регрессии
· Число степеней свободы, связанных с дисперсией адекватности:
· Дисперсия адекватности
· Вычисление расчетного коэффициента Фишера:
· Табличный коэффициент Фишера
Поскольку Проверка эффективности оценивают в следующей последователь-ности.
· Выборочное среднее по всем сериям опытов
· Вычисление дисперсии относительно среднего значения отклика
· Вычисление остаточной дисперсии
· Вычисление отношения Регрессионная модель считается эффективной, если Графики функции
а) б)
Из графика видно, что данная зависимость является плоскостью в трехмерном пространстве. Из графиков, рисунок 3.6, хорошо видно, что с увеличением фактора Чтобы оценить влияние взаимодействия факторов
Таблица 3.6
Тогда коэффициент
Теперь модель будет иметь вид
Проверим значимость коэффициента
Расчетный коэффициент
Коэффициент План эксперимента можно записать с буквенными обозначениями уровней факторов, таблица 3.7.
Таблица 3.7
Здесь комбинации факторов на различных уровнях: (1) a b ab
Такая запись матрицы плана полного факторного эксперимента значительно сокращает ее запись, особенно в том случае, когда количество факторов достаточно велико. Например, матрица ПФЭ для 3-х факторов будет иметь вид, таблица 3.8. Таблица 3.8
Как видно из таблицы 9, запись матрицы ПФП в буквенных обозначениях для трех факторов значительно меньше матрицы со значениями
3.8. Дробный факторный эксперимент [1, 3, 5, 24, 26, 36] Количество опытов в полном факторном плане быстро увеличивается при увеличении количества варьируемых факторов Такой эксперимент называется дробным факторным экспериментом (ДФЭ). Этот план ДФЭ обозначается как
Например, для ДФЭ
(3.38)
Таблица 3.9
Коэффициент регрессии со смешанными оценками могут удовлетворительно оценивать соответствующий истинный коэффициент, при условии, что второй эффект отсутствует, то есть его коэффициент незначимо отличается от нуля. План дробного факторного эксперимента типа Если в эксперимент включить еще один фактор, приравняв его к какому-нибудь взаимодействию факторов, например,
При введении еще одного фактора, например, В ДФЭ типа Генерирующим соотношением или генератором плана называется соотношение, в котором в левой части стоит новый фактор, а в правой – произведение некоторых взаимодействий факторов, то есть генерирующее соотношение показывает, какие взаимодействия заменены новыми факторами. Возникает необходимость выбрать, такое из восьми взаимодействий лучше выбрать для построения ДФД Определяющим контрастом называется соотношение, определенное как символическое произведение столбцов плана, равное +1 или
С помощью определяющего контраста можно легко получить систему смешивания эффектов взаимодействия факторов. Пусть необходимо определить систему смешивания оценок для генерирующего соотношения
Из полученного соотношения получаем следующую систему смешивания оценок:
Таким образом, для рассматриваемых генераторов плана будем иметь следующие оценки:
В шести указанных планах все линейные эффекты Дробные реплики с одинаковым количеством опытов могут иметь различные разрешающие способности. Например, для плана эксперимента
Какую реплику следует выбрать из восьми возможных? Если необходимо более точно определить линейные эффекты, при условии, что тройные и взаимодействия более высокого порядка незначимы, можно выбрать полуреплику Если нужно, чтобы линейные эффекты оценивались независимо от парных взаимодействий, необходимо использовать полуреплики
(3.45) только нечетными комбинациями букв
Полуреплики, в которых новые вводимые факторы приравнивают взаимодействиям наивысших порядков, обладают максимальной разрешающей способностью Для полуреплики Если взять, например, полуреплику с ОК Для полуреплики с ОК Введя новый фактор Чтобы полностью охарактеризовать разрешающую способность четверть реплики, вводится понятие обобщающего определяющего контраста (ООК). В нашем примере третий определяющий контраст получается перемножением двух исходных
Этот план имеет разрешающую способность
Основные эффекты, без парных взаимодействий, можно получить, добавив новую четверть-реплику с ООК
Реплики большой дробности Процедура выбора реплики большой дробности совершенно аналогична, рассмотренной ранее. Пусть необходимо провести эксперимент по ДФП с числом факторов
В таблице 3.10 приведены зависимости количества основных опытов от дробности реплики. Таблица 3.10
Для каждого из этих решений можно сделать шесть перестановок. В итоге мы получаем 24 возможности выбора 1/8 Наименее удачным будет выбор номер один, поскольку в нем линейные эффекты смешиваются с парными взаимодействиями. Если априори известно, что взаимодействие Пусть мы выбрали четвертое решение, полагая, что фактор
При этом мы ограничимся парными и тройными взаимодействиями факторов. Для 1/8
и определяющими контрастами:
Если попарно перемножить эти определяющие контрасты, то получим:
Произведение трех определяющих контрастов будет равно Чтобы полностью охарактеризовать разрешающую способность этой 1/8
Получается следующая система смешивания:
С ростом числа факторов дробность реплик увеличивается и усложняется система смешивания оценок. Предельное число факторов для восьми опытов – семь. В этом случае оцениваются восемь коэффициентов линейного уравнения
число степеней свободы С ростом числа факторов от 8 до 15 необходимо ставить 16 опытов. Предельное число факторов для 16 опытов – пятнадцать. План с максимальным числом факторов для данного числа опытов и заданной модели называется насыщенным. В этом случае число основных опытов равно числу оцениваемых коэффициентов регрессии Пример. Пусть задана матрица плана ДФЭ для трех факторов
Таблица 3.11 ДФЭ
Здесь Вычисляются оценки коэффициентов регрессии:
Регрессионная математическая модель в данном случае будет иметь вид
Вычисление предсказанных значений функции отклика для всех основных опытов:
Проверка однородности дисперсий по сериям дублированных опытов:
Вычисление расчетного коэффициента Кохрена
Табличный коэффициент Кохрена Поскольку Вычисляем дисперсию воспроизводимости
Вычисляем дисперсии коэффициентов регрессии:
Проверяем значимость коэффициентов регрессионной математической модели:
Поскольку
Поскольку план эксперимента насыщенный, проверить адекватность математической модели невозможно. В рассматриваемом плане генерирующим соотношением будет
Разрешающая способность этой дробной реплики будет равна
|
||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 1360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.209.144 (0.012 с.) |

 основных опытов экспериментального плана и
основных опытов экспериментального плана и 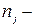 число параллельных (дублированных) опытов в каждом
число параллельных (дублированных) опытов в каждом 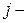 ом основном опыте,
ом основном опыте,  число оцениваемых коэффициентов регрессии в математической модели.
число оцениваемых коэффициентов регрессии в математической модели. больше числа коэффициентов регрессии
больше числа коэффициентов регрессии 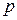 ,
, 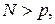 то такой план эксперимента называется не насыщенным и в этом случае можно проверить адекватность математической модели. В противном случае,
то такой план эксперимента называется не насыщенным и в этом случае можно проверить адекватность математической модели. В противном случае,  проверить адекватность невозможно.
проверить адекватность невозможно. и полученными в результате расчетов по уравнению регрессии
и полученными в результате расчетов по уравнению регрессии  ;
;


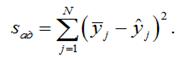
 дисперсии адекватности
дисперсии адекватности (3.29)
(3.29) (3.30)
(3.30) и воспроизводимости
и воспроизводимости 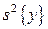
 (3.31)
(3.31) сравнивают с
сравнивают с 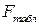 , выбранном при уровне значимости
, выбранном при уровне значимости 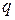 и числах степеней свободы
и числах степеней свободы 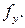 Если выполняется условие
Если выполняется условие  то модель можно считать адекватной исследуемому объекту.
то модель можно считать адекватной исследуемому объекту.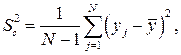 (3.32)
(3.32) среднее значение функции отклика по всем опытам.
среднее значение функции отклика по всем опытам. :
:

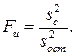 (3.34)
(3.34)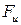 показывает, во сколько раз уравнение регрессии точнее описывает результаты эксперимента по сравнению со средним значением
показывает, во сколько раз уравнение регрессии точнее описывает результаты эксперимента по сравнению со средним значением 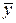 . Модель считается эффективной, если
. Модель считается эффективной, если 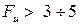 раз.
раз.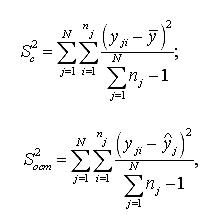 Для экспериментов с дублированными опытами формулы для вычисления
Для экспериментов с дублированными опытами формулы для вычисления  рассчитываются по следующим формулам:
рассчитываются по следующим формулам: значение выходной величины в
значение выходной величины в 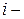 ом дублированном опыте
ом дублированном опыте  (3.36)
(3.36)




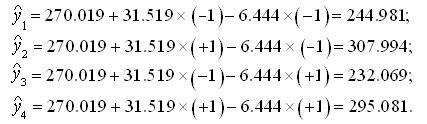
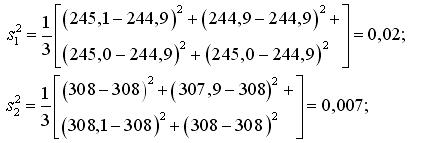
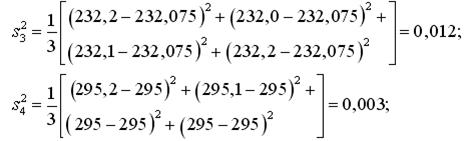
 :
:
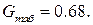
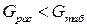 (
(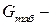 табличное значение коэффициента Кохрена), то гипотеза об однородности дисперсий принимается.
табличное значение коэффициента Кохрена), то гипотеза об однородности дисперсий принимается.



 меньше
меньше  все коэффициенты значимы.
все коэффициенты значимы. :
:


 :
:
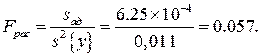

 то математическая модель адекватна.
то математическая модель адекватна.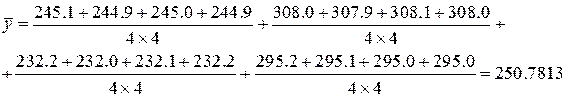


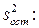

 .
.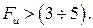 В данном случае это условие выполнено.
В данном случае это условие выполнено. представлены на рисунке 3.6.
представлены на рисунке 3.6.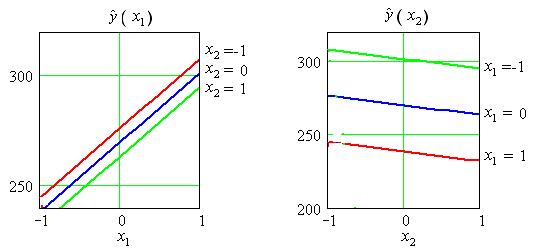


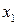 выходная величина увеличивается (коэффициент
выходная величина увеличивается (коэффициент  ), с увеличением фактора
), с увеличением фактора 
 уменьшается (коэффициент
уменьшается (коэффициент 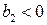 ).
). на выходную величину
на выходную величину  , необходимо в таблицу 6 ввести еще один столбец, таблица 3.6.
, необходимо в таблицу 6 ввести еще один столбец, таблица 3.6.
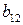 рассчитывается по формуле:
рассчитывается по формуле: .
.

 больше табличного
больше табличного 
 - все факторы на нижнем уровне;
- все факторы на нижнем уровне; - первый фактор на верхнем уровне;
- первый фактор на верхнем уровне; - второй фактор на верхнем уровне;
- второй фактор на верхнем уровне;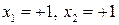 - оба фактора на верхнем уровне.
- оба фактора на верхнем уровне.
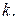 Например, при
Например, при 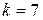 число основных опытов
число основных опытов  Если, например, количество дублированных опытов
Если, например, количество дублированных опытов  , число опытов станет равным
, число опытов станет равным  Такое количество экспериментов естественно совершенно недопустимо, особенно на начальном этапе экспериментального исследования. Поэтому необходимо найти способ сокращения количества экспериментов. Решение этой задачи подсказывает тот факт, что многие взаимодействия факторов лишь незначительно, а и то вовсе не влияют на выходную величину. Поэтому некоторое взаимодействие факторов можно заменить новым фактором, например,
Такое количество экспериментов естественно совершенно недопустимо, особенно на начальном этапе экспериментального исследования. Поэтому необходимо найти способ сокращения количества экспериментов. Решение этой задачи подсказывает тот факт, что многие взаимодействия факторов лишь незначительно, а и то вовсе не влияют на выходную величину. Поэтому некоторое взаимодействие факторов можно заменить новым фактором, например,  . И тогда вместо плана полного факторного эксперимента с четырьмя факторами (
. И тогда вместо плана полного факторного эксперимента с четырьмя факторами (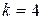 ) можно использовать матрицу плана с тремя факторами (
) можно использовать матрицу плана с тремя факторами ( ). Это позволяет вместо
). Это позволяет вместо  основных опытов поставить эксперимент с
основных опытов поставить эксперимент с  опытами, то есть количество опытов сократится вдвое. Это будет, так называемый, дробный факторный план (ДФП). Матрица ДФП представлена в таблице 10.
опытами, то есть количество опытов сократится вдвое. Это будет, так называемый, дробный факторный план (ДФП). Матрица ДФП представлена в таблице 10. . В плане ДФЭ
. В плане ДФЭ 
 столбец
столбец  столбец
столбец  и т. д. Отсюда следует, что оценки коэффициентов будут смешанными, то есть они являются совместными оценками двух эффектов:
и т. д. Отсюда следует, что оценки коэффициентов будут смешанными, то есть они являются совместными оценками двух эффектов: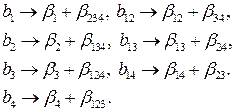 (3.37)
(3.37) можно составить следующие восемь генерирующих соотношений:
можно составить следующие восемь генерирующих соотношений: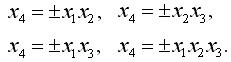

 называется полурепликой от полного факторного эксперимента
называется полурепликой от полного факторного эксперимента 
 получим четверть
получим четверть 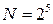 или
или  Система смешивания оценок будет иметь вид
Система смешивания оценок будет иметь вид (3.39)
(3.39)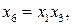 получим ДФП типа
получим ДФП типа  реплики ПФЭ
реплики ПФЭ  и т. д.
и т. д. каждая из групп содержит
каждая из групп содержит 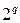 смешанных эффектов взаимодействия факторов.
смешанных эффектов взаимодействия факторов.
 (3.40)
(3.40)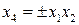 с определяющим контрастом
с определяющим контрастом  поскольку
поскольку 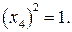 Для этого необходимо умножить правую часть определяющего контраста на
Для этого необходимо умножить правую часть определяющего контраста на  (3.41)
(3.41) (3.42)
(3.42) (3.43)
(3.43) смешаны только с парными взаимодействиями
смешаны только с парными взаимодействиями  и могут быть оценены независимо, если парные взаимодействия равны нулю. Реплики, в которых линейные эффекты смешаны с парными взаимодействиями, называются планами с разрешающей способностью R=III (по количеству факторов в определяющем контракте).
и могут быть оценены независимо, если парные взаимодействия равны нулю. Реплики, в которых линейные эффекты смешаны с парными взаимодействиями, называются планами с разрешающей способностью R=III (по количеству факторов в определяющем контракте). (3.44)
(3.44) с
с  или
или  то есть с генерирующими соотношениями
то есть с генерирующими соотношениями  или
или  Количество факторов в ОК этой реплики
Количество факторов в ОК этой реплики 
 с определяющими контрастами
с определяющими контрастами 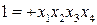 или
или  с количеством членов
с количеством членов  для генерирующих соотношений
для генерирующих соотношений  . Эти полуреплике записываются только четными комбинациями букв
. Эти полуреплике записываются только четными комбинациями букв
 (3.46)
(3.46)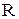 . Они называются главными полурепликами.
. Они называются главными полурепликами. будут главными, поскольку они имеют максимальное число факторов.
будут главными, поскольку они имеют максимальное число факторов. то система смешивания оценок будет
то система смешивания оценок будет 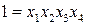 система смешивания оценок будет
система смешивания оценок будет  В этой полуреплике основные эффекты связаны с тройными взаимодействиями. В общем случае
В этой полуреплике основные эффекты связаны с тройными взаимодействиями. В общем случае  будет меньше
будет меньше  (
( ), потому предпочтение отдается полуреплике с ОК
), потому предпочтение отдается полуреплике с ОК 
 , можно получить четверть-реплику
, можно получить четверть-реплику  . Пусть
. Пусть 
 то есть
то есть  а их ООК будет иметь вид:
а их ООК будет иметь вид: (3.47)
(3.47) поскольку два ОК содержат по три члена. Коэффициенты регрессии будут являться совместными оценками:
поскольку два ОК содержат по три члена. Коэффициенты регрессии будут являться совместными оценками: (3.48)
(3.48) в которой факторы заменены на обратные. Этот метод называется «методом перевала». В результате получаем из реплики с разрешающей способности
в которой факторы заменены на обратные. Этот метод называется «методом перевала». В результате получаем из реплики с разрешающей способности  реплику с разрешающей способностью
реплику с разрешающей способностью 
 При этом надо выбрать 1/8-реплики
При этом надо выбрать 1/8-реплики  . Замена факторов
. Замена факторов  , например, осуществляется следующим образом:
, например, осуществляется следующим образом: (3.49)
(3.49)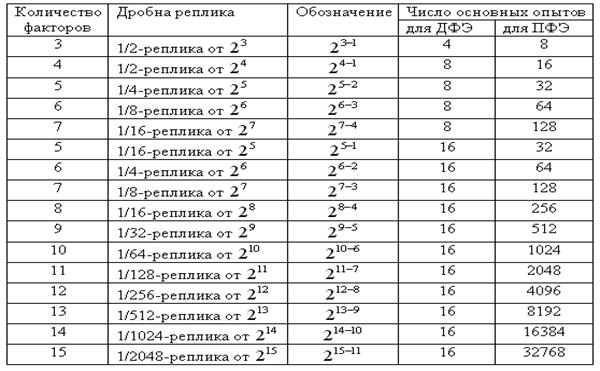
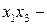 третье, если
третье, если  четвертое.
четвертое.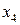 является наиболее существенным. Приравняем
является наиболее существенным. Приравняем 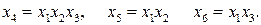 (3.50)
(3.50) (3.51)
(3.51) (3.52)
(3.52) (2.53)
(2.53)
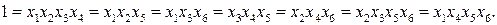 (3.54)
(3.54) (3.55)
(3.55) (3.56)
(3.56) равно нулю
равно нулю  .
. Поэтому адекватность такой модели проверить нельзя.
Поэтому адекватность такой модели проверить нельзя. (полуреплика от ПФП
(полуреплика от ПФП 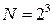 ), таблица 3.11.
), таблица 3.11.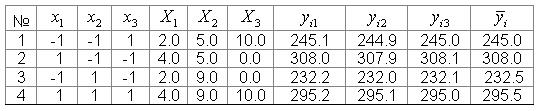
 – факторы в нормализованных значениях;
– факторы в нормализованных значениях; 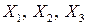 -факторы в натуральных значениях;
-факторы в натуральных значениях;  – значения выходной величины в дублированных опытах
– значения выходной величины в дублированных опытах 
 – средние значения выходной величины в основных опытах.
– средние значения выходной величины в основных опытах.
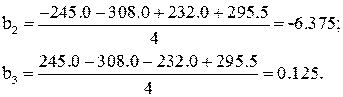






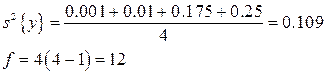


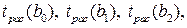 коэффициенты
коэффициенты  значимы. Коэффициент
значимы. Коэффициент  незначим. Графики зависимостей функции отклика от каждого из варьируемых факторов представлены на рисунке 23.
незначим. Графики зависимостей функции отклика от каждого из варьируемых факторов представлены на рисунке 23.

 , определяющий контраст
, определяющий контраст  Умножая последовательно определяющий контраст на
Умножая последовательно определяющий контраст на 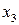 , получим следующую систему смешивания оценок:
, получим следующую систему смешивания оценок: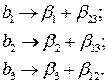 (3.57)
(3.57)


