
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решения задачи оптимального управления при наличии интегральных ограничений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В настоящем разделе рассматривается решение ЗОУ на основе вариационного метода при наличии интегральных ограничений [6]. В этой задаче минимизируется функционал:
Исходные данные и ограничения имеют следующий вид:
Здесь
Ограничение (1.33) называется дифференциальной связью. Четверка В приведенной постановке задачи оптимального управления в отличие от рассмотренный ранее присутствуют ограничения (1.35) в виде равенств, называемые изопериметрическими, и ограничения (1.34) в виде неравенств. Форма задания ограничений является достаточно общей и может включать в себя как ограничения на вид траектории движения объекта и управляющего воздействия, представленные функцией
Рассматриваемая задача содержит ограничения в форме (1.33), (1.34), (1.35), и поэтому является задачей на условный экстремум функционала. Для перехода к задаче на безусловный экстремум формируем лагранжиан и новый критерий оптимизации
Необходимые условия для решения поставленной задачи сформулированы в следующей теореме [6]. Теорема 1.5. Пусть Тогда обязательно существуют множители Лагранжа а) стационарности по
б) трансверсальности по
в) стационарности по
г) стационарности по
д) дополняющей нежесткости:
е) неотрицательности:
Доказательство теоремы приведено в [6],[2]. Набор условий теоремы для нахождения оптимального процесса является полным. Для определения неизвестных функций Для задач с закрепленными концами
Соотношения (1.43) и (1.44) не содержат граничные условия, и поэтому условия на концах траектории можно использовать при решении оптимизационной задачи самостоятельно. Пример Требуется определить оптимальное управление
Критерий оптимизации
Решение Сделаем замену переменных
Составим лагранжиан и критерий оптимизации
Запишем необходимые условия экстремума: а) система уравнений Эйлера для лагранжиана
б) условия трансверсальности по
в) условия стационарности по управлению
Для решения задачи необходимо определить значение
Общее решение этого дифференциального уравнения
Поскольку
Неизвестные константы
Следовательно, оптимальная траектория
Подставим
Итак, мы нашли оптимальную пару
Глава II. ПРИНЦИП МАКСИМУМА
Принцип максимума был разработан академиком Понтрягиным Л.С. и его учениками и впервые опубликован в 1956 году. Открытие этого принципа явилось итогом работ авторов по решению задач оптимального управления в вариационной постановке применительно к реальным объектам управления при ограниченных возможностях управляющих воздействий. Так, при решении задачи Лагранжа рассматриваются только непрерывные управляющие воздействия
|
||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 587; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.32.243 (0.007 с.) |

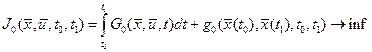 (1.32)
(1.32)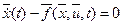 ; (1.33)
; (1.33)
 ; (1.34)
; (1.34)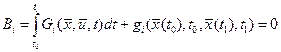
 ; (1.35)
; (1.35)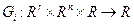 - функция
- функция 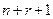 переменных;
переменных;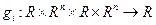 - функция
- функция 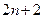 переменных;
переменных;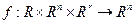 - вектор-функция
- вектор-функция 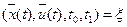 называется управляемым процессом, если
называется управляемым процессом, если  ,
, 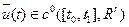 , и всюду при
, и всюду при  выполняется дифференциальная связь (1.33) и допустимым управляемым процессом, если эта четверка является управляемым процессом и, кроме того, выполнены ограничения (1.34) и (1.35). Допустимый управляемый процесс
выполняется дифференциальная связь (1.33) и допустимым управляемым процессом, если эта четверка является управляемым процессом и, кроме того, выполнены ограничения (1.34) и (1.35). Допустимый управляемый процесс  называется локальным минимумом в задаче (1.32), если существует такое
называется локальным минимумом в задаче (1.32), если существует такое 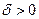 , что для любого допустимого управляемого процесса
, что для любого допустимого управляемого процесса 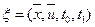 , удовлетворяющего условию
, удовлетворяющего условию  , выполняется неравенство
, выполняется неравенство 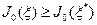 .
.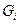 , так и краевые условия
, так и краевые условия  и
и  , которые можно записать в форме (1.35):
, которые можно записать в форме (1.35):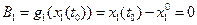 ;
; 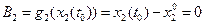
 , относительного которого ЗОУ решается как задача на безусловный экстремум.
, относительного которого ЗОУ решается как задача на безусловный экстремум.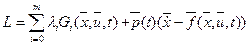 (1.36)
(1.36)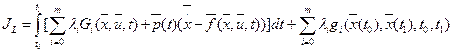
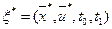 - оптимальный процесс в задаче и при этом функции
- оптимальный процесс в задаче и при этом функции 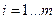 ,
, 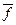 и их частные производные по
и их частные производные по 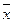 и
и 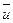 непрерывны в некоторой окрестности множества
непрерывны в некоторой окрестности множества 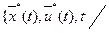
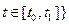 , а
, а 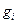 ,
, 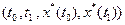 (условие гладкости).
(условие гладкости).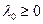 ,
, 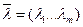 и
и 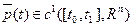 не равные одновременно нулю и такие, что для функции Лагранжа
не равные одновременно нулю и такие, что для функции Лагранжа 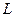 выполняются условия:
выполняются условия: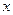 - уравнение Эйлера:
- уравнение Эйлера: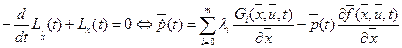 ; (1.37)
; (1.37)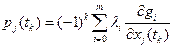 ,
,  ; (1.38)
; (1.38)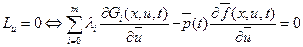 ; (1.39)
; (1.39) :
: ; (1.40)
; (1.40)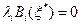 ,
, 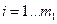 ; (1.41)
; (1.41)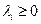 ,
,  . (1.42)
. (1.42)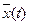 ,
, 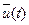 и
и 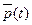 имеется система из дифференциальных уравнений из (1.34), (1.37) и (1.40). Выразим
имеется система из дифференциальных уравнений из (1.34), (1.37) и (1.40). Выразим  скалярных дифференциальных уравнений. Решение системы зависит от 2 n произвольных постоянных и еще множители
скалярных дифференциальных уравнений. Решение системы зависит от 2 n произвольных постоянных и еще множители 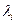 ,
,  . Кроме того, решение задачи требует определения
. Кроме того, решение задачи требует определения 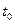 и
и 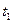 . Следовательно, всего неизвестных
. Следовательно, всего неизвестных 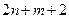 . Для их определения имеется 2
. Для их определения имеется 2 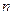 условий трансверсальности,
условий трансверсальности,  условий дополняющей нежесткости и заданных ограничений (1.35) и два условия стационарности по
условий дополняющей нежесткости и заданных ограничений (1.35) и два условия стационарности по  и
и 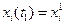 ,
, 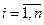 условия трансверсальности тоже можно написать, если принять
условия трансверсальности тоже можно написать, если принять 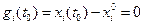 ,
,  ,
,  , и эти условия можно рассматривать как соотношение (1.35) в постановке задачи оптимизации. В этом случае условия трансверсальности имеют вид [8]:
, и эти условия можно рассматривать как соотношение (1.35) в постановке задачи оптимизации. В этом случае условия трансверсальности имеют вид [8]: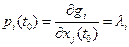 ,
, 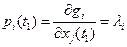 ,
,  в задаче, имеющей следующие исходные данные:
в задаче, имеющей следующие исходные данные: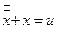 ,
, 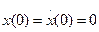 ,
, 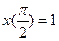 ,
,
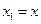 и
и 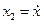 , чтобы представить описание объекта в переменных состояния:
, чтобы представить описание объекта в переменных состояния: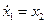 ,
, 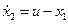 ,
, 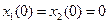 ,
, 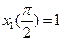 ,
, 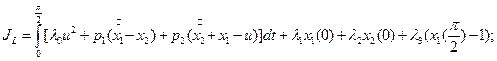
 ;
;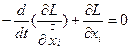 ,
, 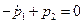 ,
, 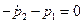 ;
; ;
;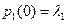 ,
, 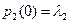 ,
, 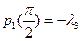 ,
,  ;
;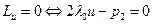 .
.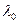 . Если принять
. Если принять 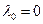 , то из в) следует, что
, то из в) следует, что 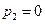 , тогда из а) имеем
, тогда из а) имеем  и в силу условия б) получаем
и в силу условия б) получаем  , т.е. все множители Лагранжа равны нулю, что противоречит условию теоремы о необходимом условии экстремума. Положим
, т.е. все множители Лагранжа равны нулю, что противоречит условию теоремы о необходимом условии экстремума. Положим 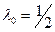 . Из системы уравнений Эйлера вытекает, что
. Из системы уравнений Эйлера вытекает, что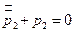
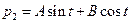 .
.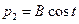 и по условию стационарности по управлению
и по условию стационарности по управлению  . Тогда дифференциальное уравнение связи и его решение имеет вид:
. Тогда дифференциальное уравнение связи и его решение имеет вид: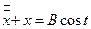 ;
;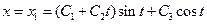 .
.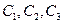 определяются из заданных условий на концах:
определяются из заданных условий на концах: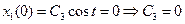 ;
; 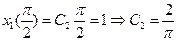 ;
; 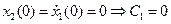 ;
;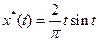 ;
;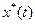 в уравнение связи и получим функцию оптимального управления
в уравнение связи и получим функцию оптимального управления 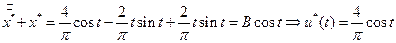 ;
;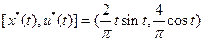 . Можно показать с помощью непосредственной проверки, что найденный экстремум является абсолютным минимумом.
. Можно показать с помощью непосредственной проверки, что найденный экстремум является абсолютным минимумом. без ограничений на максимальное и минимальное значение. В практических ситуациях управляющее воздействие всегда ограничено по модулю, а иногда все множество допустимых значений
без ограничений на максимальное и минимальное значение. В практических ситуациях управляющее воздействие всегда ограничено по модулю, а иногда все множество допустимых значений  состоит из совокупности точек. Кроме того, известно, что ряд оптимизационных задач имеет решение
состоит из совокупности точек. Кроме того, известно, что ряд оптимизационных задач имеет решение  возможных значений управления считается произвольным топологическим пространством, не обладающим в общем случае линейной структурой, в реализации условий принципа максимума. Отсутствуют требования на существование производных по
возможных значений управления считается произвольным топологическим пространством, не обладающим в общем случае линейной структурой, в реализации условий принципа максимума. Отсутствуют требования на существование производных по 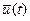 функций
функций 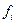 . Однако при решении задач оптимального управления эта особенность метода восполняется необходимостью решения вспомогательной задачи на максимум по переменной
. Однако при решении задач оптимального управления эта особенность метода восполняется необходимостью решения вспомогательной задачи на максимум по переменной 


