Глава I. Решение задачи оптимального управления на основе вариационного исчисления и метода множителей Лагранжа.
Похожие статьи вашей тематики
Метод множителей Лагранжа.
Задачи на определение координат экстремума ( ) функции многих переменных ) функции многих переменных 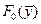 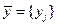  принято называть экстремальными. При этом возможны два варианта постановки задачи. Допустимая область существования принято называть экстремальными. При этом возможны два варианта постановки задачи. Допустимая область существования 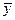 , в которой ищется , в которой ищется  , обеспечивающий , обеспечивающий 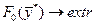 не ограничена. Такие задачи называются задачами на безусловный экстремум. Согласно определению функция не ограничена. Такие задачи называются задачами на безусловный экстремум. Согласно определению функция 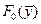 имеет в точке имеет в точке  минимум (максимум) если выполняется неравенство минимум (максимум) если выполняется неравенство
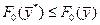 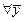 (минимум) (минимум)  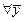 (максимум) (1.1) (максимум) (1.1)
Правило решения таких задач сформулировано в теореме Ферма.
Теорема 1.1 Пусть функция многих переменных 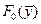 дифференцируема в точке дифференцируема в точке  . Для того, чтобы в этой точке . Для того, чтобы в этой точке  существовал экстремум (минимум или максимум) функции существовал экстремум (минимум или максимум) функции 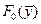 необходимо выполнение условия необходимо выполнение условия
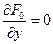 при при 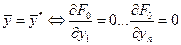 при при 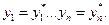 (1.2) (1.2)
Доказательство теоремы основывается на том факте, что при малом изменении какого-либо аргумента, например, придания 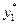 значения значения 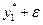 , значение функции , значение функции 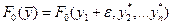 описывается соотношением описывается соотношением
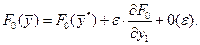 (1.3) (1.3)
Далее делается допущение, что  является точкой минимума является точкой минимума  . Выбирая . Выбирая  достаточно малым и придавая ему произвольный знак, всегда можно добиться того, чтобы условие (1.1) было нарушено, если не выполнено условие (1.2), что противоречит прямому допущению. Точки достаточно малым и придавая ему произвольный знак, всегда можно добиться того, чтобы условие (1.1) было нарушено, если не выполнено условие (1.2), что противоречит прямому допущению. Точки  , в которых выполняется соотношение (1.2), называют стационарными. , в которых выполняется соотношение (1.2), называют стационарными.
Если  принадлежит ограниченной области принадлежит ограниченной области 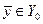 и и  не является внутренней точкой не является внутренней точкой 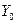 , то условие (1.2) не является необходимым. Например, пусть допустимыми являются только значения , то условие (1.2) не является необходимым. Например, пусть допустимыми являются только значения  и точка и точка  такова, что какая-либо компонента, например, такова, что какая-либо компонента, например, 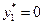 . Тогда в этой точке может достигаться минимум, если даже . Тогда в этой точке может достигаться минимум, если даже 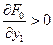 , что также прямо следует из (1.3), поскольку в этой формуле можно выбирать только , что также прямо следует из (1.3), поскольку в этой формуле можно выбирать только 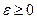 . Как правило, допустимая область . Как правило, допустимая область 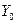 явно задается с помощью системы условий в виде уравнений или неравенств, которым должны удовлетворять значения явно задается с помощью системы условий в виде уравнений или неравенств, которым должны удовлетворять значения 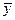 . Кратко это можно записать в виде: . Кратко это можно записать в виде:
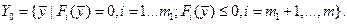 (1.4) (1.4)
Экстремальная задача при наличии ограничений на 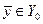 называется задачей на условный экстремум. Если определен экстремум функции при наличии ограничений, то этот экстремум называется условным (локальным). называется задачей на условный экстремум. Если определен экстремум функции при наличии ограничений, то этот экстремум называется условным (локальным).
Для решения задач на экстремум функции многих переменных французским математиком Лагранжем в  веке был предложен метод, который получил название «метод множителей Лагранжа». веке был предложен метод, который получил название «метод множителей Лагранжа».
Пусть ограничения на область 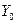 имеют форму равенств имеют форму равенств  , требуется определить , требуется определить
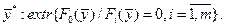 (1.5) (1.5)
Для решения задачи составляется функция Лагранжа (лагранжиан) 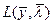 как сумма экстремизируемой функции как сумма экстремизируемой функции 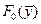 и функций ограничения и функций ограничения 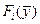 умноженных на множители Лагранжа умноженных на множители Лагранжа 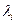 , , 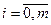 : :
 (1.6) (1.6)
Далее, согласно методу Лагранжа решается задача на экстремум функции 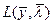 без ограничений. Следовательно, метод Лагранжа позволяет свести задачу на условный экстремум к задаче на безусловный экстремум. Сформулированная ниже теорема показывает что стационарные точки исходной и приведенной задачи совпадают. Однако, надо отметить, что вид экстремума (min или max, точка перегиба) может не совпадать. без ограничений. Следовательно, метод Лагранжа позволяет свести задачу на условный экстремум к задаче на безусловный экстремум. Сформулированная ниже теорема показывает что стационарные точки исходной и приведенной задачи совпадают. Однако, надо отметить, что вид экстремума (min или max, точка перегиба) может не совпадать.
Теорема 1.2. Пусть в задаче (1.5) все функции 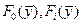  непрерывно дифференцируемы в окрестности точки непрерывно дифференцируемы в окрестности точки  . Если . Если  - точка локального экстремума в задаче (1.5), то необходимо существование множителей Лагранжа - точка локального экстремума в задаче (1.5), то необходимо существование множителей Лагранжа 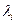 , , 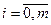 не равных одновременно нулю и таких, что выполняются условия стационарности функции Лагранжа по не равных одновременно нулю и таких, что выполняются условия стационарности функции Лагранжа по 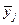 . .
 при при  
(1.7)
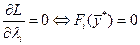 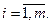
Если при этом выполняются условия регулярности 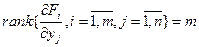 , то заведомо существуют такие , то заведомо существуют такие 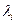 , причем , причем  [2]. Нужно заметить, что множители Лагранжа определены с точностью до пропорциональности. Если известно, что [2]. Нужно заметить, что множители Лагранжа определены с точностью до пропорциональности. Если известно, что  , то можно, умножив все , то можно, умножив все 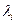 на константу, добиться равенства на константу, добиться равенства  . Тогда число уравнений (1.7) сравняется с числом неизвестных. Согласно содержанию метода Лагранжа, точки . Тогда число уравнений (1.7) сравняется с числом неизвестных. Согласно содержанию метода Лагранжа, точки  являются подозрительными на экстремум. Для того, чтобы выяснить, будет ли в этих точках в действительности реализовываться локальный минимум, максимум или точка перегиба, нужно провести дополнительные исследования либо путем привлечения вторых производных функций Лагранжа по переменной являются подозрительными на экстремум. Для того, чтобы выяснить, будет ли в этих точках в действительности реализовываться локальный минимум, максимум или точка перегиба, нужно провести дополнительные исследования либо путем привлечения вторых производных функций Лагранжа по переменной 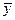 , либо путем вычисления , либо путем вычисления 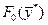 . .
Теперь рассмотрим вопрос применения метода множителей Лагранжа при наличии ограничений в виде неравенств. Для определенности рассмотрим задачу:
определить 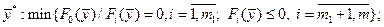 (1.8) (1.8)
где 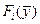 - гладкие функции, - гладкие функции,  . Путем введения новых переменных . Путем введения новых переменных 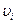 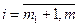 превратим ограничения неравенства в уравнения: превратим ограничения неравенства в уравнения:
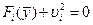 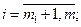 (1.9) (1.9)
Переменная 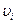 берется в квадрате для того, чтобы не вводить ограничения на ее знак, обеспечивающий равенство (1.9). Решение задачи (1.8) с учетом (1.9) проводим по вышеописанной методике. Составляем расширенный лагранжиан: берется в квадрате для того, чтобы не вводить ограничения на ее знак, обеспечивающий равенство (1.9). Решение задачи (1.8) с учетом (1.9) проводим по вышеописанной методике. Составляем расширенный лагранжиан:
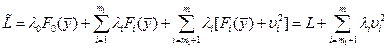 , , 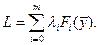 (1.10) (1.10)
Функция  , в отличие от , в отличие от 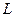 , зависит от переменных , зависит от переменных 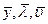 . Необходимые условия безусловного экстремума . Необходимые условия безусловного экстремума 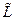 состоят из следующих уравнений: состоят из следующих уравнений:
Условия минимума 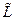 по по 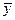 : :
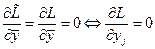 , ,  (1.11) (1.11)
Условия минимума по 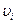
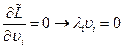 , , 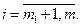 (1.12) (1.12)
При этом минимум достигается только при условии
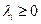 , , 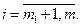 (1.13) (1.13)
Ограничения (1.13) называются условиями неотрицательности. Они имеют тот же смысл, что и в линейном программировании. При отсутствии ограничения на величину  (всегда положительного слагаемого) и при решении задачи на минимум функции (всегда положительного слагаемого) и при решении задачи на минимум функции 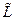 отрицательное значение отрицательное значение 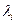 дает дает 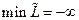 . Условия (1.12) означают, что в точке минимума либо . Условия (1.12) означают, что в точке минимума либо 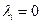 , либо , либо 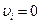 , т.е. с учетом (1.9): , т.е. с учетом (1.9):
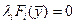 , , 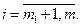 (1.14) (1.14)
Эти условия обычно называют условиями дополняющей нежесткости (если какое-либо неравенство выполняется в точке минимума  нежестко, т.е. точка нежестко, т.е. точка  не лежит на поверхности, определенной условием (1.9), то соответствующий множитель не лежит на поверхности, определенной условием (1.9), то соответствующий множитель 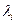 должен быть жестко равен нулю или наоборот). Строгий результат может быть сформулирован в виде теоремы [3]. должен быть жестко равен нулю или наоборот). Строгий результат может быть сформулирован в виде теоремы [3].
Теорема 1.3. Для того, чтобы в точке  достигался минимум функции достигался минимум функции 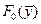 в области в области
 , необходимо, чтобы существовали числовые множители , необходимо, чтобы существовали числовые множители 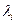 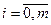 , , 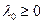 , не равные одновременно нулю, и такие, чтобы они совместно с , не равные одновременно нулю, и такие, чтобы они совместно с 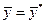 удовлетворяет системе условий: удовлетворяет системе условий:
  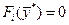 
(1.15)
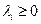 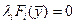 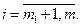
Функции 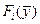 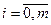 предполагаются непрерывно дифференцируемыми в точке предполагаются непрерывно дифференцируемыми в точке  . Если, кроме того, при . Если, кроме того, при 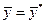 выполнено условие регулярности для выполнено условие регулярности для  , кроме таких, для которых , кроме таких, для которых 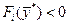 , то указанный набор множителей , то указанный набор множителей 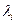 существует, причем существует, причем 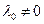 , так что функция Лагранжа может быть записана с , так что функция Лагранжа может быть записана с  . .
Уравнение Эйлера-Лагранжа.
Как показывает практика, в теории оптимального управления наиболее распространенной формой критерия оптимизации является интегральный функционал. Значение функционала определяется формой кривой подынтегральной функции. Функция, экстремизирующая функционал, называется экстремалью. Решение задачи определения экстремали было дано математиком Эйлером в середине XVIII века [2]. Аппроксимируя подынтегральные кривые ломаными, Эйлер вывел дифференциальное уравнение второго порядка, которому должны были удовлетворять экстремали. Впоследствии Лагранж назвал это уравнение уравнением Эйлера. В дальнейшем перед математиками встал вопрос решения более сложной задачи. Требуется определить экстремаль функционала при наличии ограничений в виде равенств, которым должна удовлетворять экстремаль. При решении этой задачи исследователи применили правило множителей Лагранжа, что позволило получить необходимые условия, которым должна удовлетворять искомая экстремаль. При этом уравнение Эйлера вошло в эти условия как составная часть. Далее рассмотрим вывод необходимых условий экстремума функционала при ограничениях в виде дифференциальных уравнений объекта, для которого решается задача оптимизации. Эти ограничения называются уравнениями связи. Однако прежде чем перейти к изложению вывода, напомним некоторые сведения, характеризующие понятие и свойство функционала [4].
1.2.1. Определение функционала. Если каждой функции 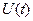 из множества из множества 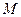 поставлено в соответствие по некоторому правилу число поставлено в соответствие по некоторому правилу число  , то говорят, что на множестве , то говорят, что на множестве 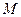 (в классе (в классе 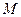 ) определен функционал ) определен функционал 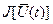 . Множество . Множество 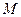 функции функции  (класс функций (класс функций  ), на котором определен функционал ), на котором определен функционал 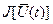 , называется областью задания функционала. , называется областью задания функционала.
Вариация аргумента функционала. Вариацией или приращением 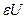 аргумента аргумента 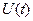 функционала функционала  называется разность между двумя функциями называется разность между двумя функциями 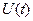 и и  из выбранного множества из выбранного множества 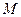 : :
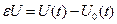 , , 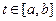 . .
Кривые 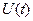 и и  , заданные на отрезке , заданные на отрезке 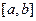 , близки в смысле близости нулевого порядка, если модуль разности , близки в смысле близости нулевого порядка, если модуль разности 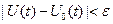 для для 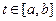 , где , где 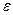 - малая величина. Геометрически это означает, что кривые при - малая величина. Геометрически это означает, что кривые при 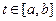 близки по ординатам. Если для этих же кривых близки по ординатам. Если для этих же кривых 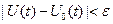 и и  при при 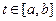 (где обозначено (где обозначено 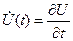 ), то кривые близки в смысле близости первого порядка. Геометрически это означает, что кривые при ), то кривые близки в смысле близости первого порядка. Геометрически это означает, что кривые при 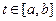 близки как по ординатам, так и по направления касательных в соответствующих точках. Кривые близки как по ординатам, так и по направления касательных в соответствующих точках. Кривые 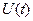 и и  близки в смысле близости близки в смысле близости 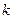 -го порядка, если выполняются неравенства: -го порядка, если выполняются неравенства:
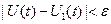 , ,  ,… ,… 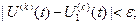
при 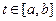 . Если кривые близки в смысле близости . Если кривые близки в смысле близости 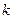 -го порядка, то они тем более близки в смысле близости любого меньшего порядка. -го порядка, то они тем более близки в смысле близости любого меньшего порядка.
Непрерывность функционала. Функционал  , определенный на множестве , определенный на множестве 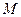 функции функции 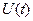 , называется непрерывным на элементе множества , называется непрерывным на элементе множества  в смысле близости в смысле близости 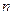 -го порядка, если для любого числа -го порядка, если для любого числа 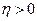 существует число существует число 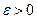 , такое, что для всех допустимых функций , такое, что для всех допустимых функций 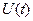 , удовлетворяющих условиям , удовлетворяющих условиям
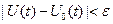 , ,  ,… ,… 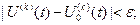
выполняется неравенство 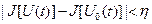 . Функционал, не являющийся непрерывным смысле близости . Функционал, не являющийся непрерывным смысле близости 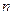 -го порядка, называется разрывным в смысле названной близости. -го порядка, называется разрывным в смысле названной близости.
Приращение функционала. Приращением функционала  , отвечающим приращению аргумента , отвечающим приращению аргумента 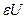 , называется величина: , называется величина:
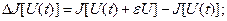  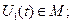 
Дифференцируемость функционала. Вариация функционала. Функционал  , заданный на множестве , заданный на множестве 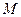 , называется дифференцируемым в точке , называется дифференцируемым в точке  , если существует такой линейный относительно приращения аргумента , если существует такой линейный относительно приращения аргумента 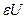 функционал функционал 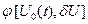 , что для любого допустимого приращения , что для любого допустимого приращения  функции функции  приращение функционала имеет вид: приращение функционала имеет вид:
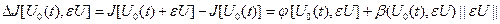
и 
При этом 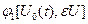 называется сильным дифференциалом (дифференциал Фреше) функционала называется сильным дифференциалом (дифференциал Фреше) функционала  или его первой вариацией и обозначается или его первой вариацией и обозначается
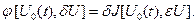 (1.16) (1.16)
Экстремум функционала. Если в окрестности точки  функционального пространства функционального пространства 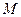 , где , где 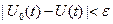 , , 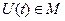 разность разность  сохранят знак, то функционал сохранят знак, то функционал  имеет локальный экстремум на кривой имеет локальный экстремум на кривой  . Если неравенство . Если неравенство 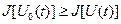 выполняется для всех кривых функционального пространства выполняется для всех кривых функционального пространства 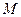 определения функционала, то на кривой определения функционала, то на кривой  достигается абсолютный максимум. Аналогично, если справедливо неравенство достигается абсолютный максимум. Аналогично, если справедливо неравенство 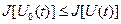 для всех кривых для всех кривых 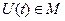 , то на кривой , то на кривой  достигается абсолютный минимум. достигается абсолютный минимум.
Теорема 1.4. Необходимое условие экстремума функционала. Если дифференцируемый функционал  имеет экстремум на имеет экстремум на  , где , где  - внутренняя точка области определения функционала, то на кривой - внутренняя точка области определения функционала, то на кривой  выполняется неравенство выполняется неравенство
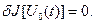 (1.17) (1.17)
Функции, для которых 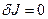 , называют стационарными функциями или стационарными точками функционального пространства задания функционала [4]. , называют стационарными функциями или стационарными точками функционального пространства задания функционала [4].
Основная лемма вариационного исчисления. Если функция 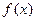 , заданная на отрезке , заданная на отрезке 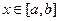 , непрерывна и для любой непрерывной функции , непрерывна и для любой непрерывной функции  , заданной на отрезке , заданной на отрезке 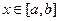 , имеет место равенство , имеет место равенство
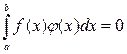 , то , то 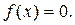
1.2.2. Вывод уравнения Эйлера-Лагранжа. Рассматривается задача Больца с закрепленными концами и безусловными ограничениями в виде дифференциальных уравнений связи. Исходные данные имеют следующий вид:
критерий оптимизации функционал 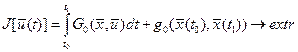
уравнения связи (уравнения объекта) 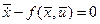 ; ; 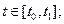 (1.18) (1.18)
граничные условия: 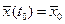 , ,  . .
Функции 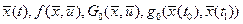 являются непрерывными и дифференцируемыми (принадлежат пространству являются непрерывными и дифференцируемыми (принадлежат пространству 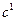 ), функция ), функция 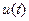 - непрерывная (принадлежит пространству - непрерывная (принадлежит пространству 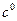 ). Постановка задачи оптимизации: ). Постановка задачи оптимизации:
определить 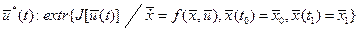 , , 
На основании метода Лагранжа перейдем от решения оптимизационной задачи на условный экстремум функционала (при наличии ограничений в виде уравнений связи) к задаче на безусловный экстремум. Для этого составим лагранжиан:
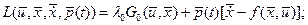 (1.19) (1.19)
где 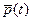 - непрерывная вектор-функция множителей Лагранжа. - непрерывная вектор-функция множителей Лагранжа.
Поскольку ограничения в виде уравнений объекта (1.18) должны быть выполнены в любой момент времени  , что фактически означает наличие бесконечного числа ограничений, числовые множители Лагранжа представляются функцией времени. , что фактически означает наличие бесконечного числа ограничений, числовые множители Лагранжа представляются функцией времени.
От первоначальной задачи 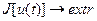 переходим к задаче: переходим к задаче:
 (1.20) (1.20)
Предположим, что оптимальное управление 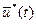 найдено. Следовательно, определена оптимальная траектория САУ найдено. Следовательно, определена оптимальная траектория САУ 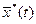 , на которой функционал (1.20) достигает экстремума. Рассмотрим его приращение за счет малой , на которой функционал (1.20) достигает экстремума. Рассмотрим его приращение за счет малой  - вариации оптимального уравнения и соответствующей ей вариации траектории системы - вариации оптимального уравнения и соответствующей ей вариации траектории системы 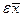 . Так как функции . Так как функции  и и  являются гладкими, малые вариации управления дают и малые вариации значения функционала являются гладкими, малые вариации управления дают и малые вариации значения функционала 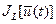 . Допустим, что функция . Допустим, что функция 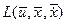 непрерывна по совокупности своих аргументов и имеет непрерывные частные производные второго порядка по всем аргументам в области непрерывна по совокупности своих аргументов и имеет непрерывные частные производные второго порядка по всем аргументам в области  , , 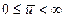 , , 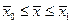 , , 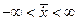 . Приращение функционала . Приращение функционала 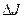 , отвечающее приращению , отвечающее приращению  аргумента, где аргумента, где  имеет вид имеет вид
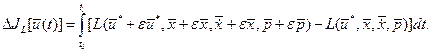 (1.21) (1.21)
В постановке оптимизационной задачи концы траектории закреплены, вариация траектории на концах недопустима, поэтому терминантный член функционала (функция 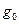 ) отсутствует в выражении (1.21). Представим разность функций под интегралом (1.21) в виде разложения Тейлора, что допустимо вследствие непрерывности функции ) отсутствует в выражении (1.21). Представим разность функций под интегралом (1.21) в виде разложения Тейлора, что допустимо вследствие непрерывности функции 
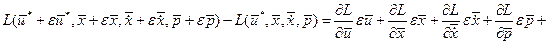
(1.22)
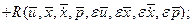
где 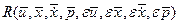 - остаточный член разложения ряда Тейлора. После подстановки (1.22) в (1.21) получим - остаточный член разложения ряда Тейлора. После подстановки (1.22) в (1.21) получим
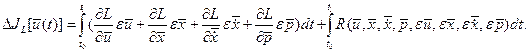 (1.23) (1.23)
Первое слагаемое в правой части (1.23) линейно относительно  и и 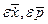 . Пусть все вторые частные производные функции . Пусть все вторые частные производные функции  по по 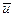 , , 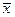 , ,  и и 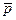 не превосходит по абсолютной величине некоторой константы не превосходит по абсолютной величине некоторой константы 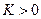 . Выберем . Выберем  таким образом, чтобы была справедлива оценка: таким образом, чтобы была справедлива оценка:
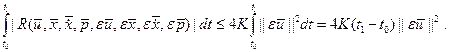 (1.24) (1.24)
Здесь 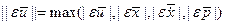 . Следовательно, второе слагаемое в правой части (1.22) – второго порядка малости относительно . Следовательно, второе слагаемое в правой части (1.22) – второго порядка малости относительно  и согласно определению функционал и согласно определению функционал  является дифференцируемым в пространстве является дифференцируемым в пространстве  и его первая вариация имеет вид: и его первая вариация имеет вид:
 (1.25) (1.25)
где 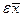 , , 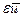 , , 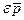 - векторы вариации траектории, управления и множителей Лагранжа соответственно. В результат интегрирования по частям третьего слагаемого в (1.25) имеем: - векторы вариации траектории, управления и множителей Лагранжа соответственно. В результат интегрирования по частям третьего слагаемого в (1.25) имеем:
 (1.26) (1.26)
Первое слагаемое в (1.26) равно нулю, так как концы  закреплены, и вариация траектории на концах исключается закреплены, и вариация траектории на концах исключается 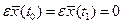 . С учетом (1.25) и (1.26) необходимое условие экстремума функционала (1.20) имеет вид: . С учетом (1.25) и (1.26) необходимое условие экстремума функционала (1.20) имеет вид:
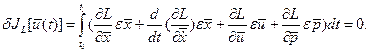 (1.27) (1.27)
В связи с тем, что вариации переменных в (1.27) произвольны, условие 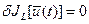 может быть выполнено, если интеграл от каждого слагаемого равен нулю. Тогда согласно основной лемме вариационного исчисления можно записать: может быть выполнено, если интеграл от каждого слагаемого равен нулю. Тогда согласно основной лемме вариационного исчисления можно записать:
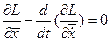 , ,  , ,  (1.28) (1.28)
Если учесть выражение для лагранжиана (1.19) то система (1.28) примет вид:
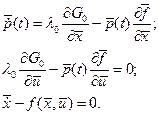 (1.29) (1.29)
Система уравнений (1.28) представляет собой необходимые условия экстремума функционала (1.20) при наличии ограничений в виде уравнений связи и называется уравнениями Эйлера-Лагранжа. Набор условий, который содержит система (1.28 или 1.29) является полным для определения всех неизвестных функций 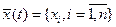 , , 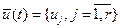 , ,  . Всего неизвестных функций . Всего неизвестных функций 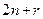 ,для их определения имеется ,для их определения имеется 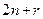 уравнений. Выражая из второго (когда это возможно) уравнений. Выражая из второго (когда это возможно) 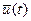 через через  и и 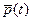 , получаем систему из , получаем систему из  скалярных дифференциальных уравнений. Ее решение зависит от скалярных дифференциальных уравнений. Ее решение зависит от  произвольных постоянных. В задачах с закрепленными концами для их определения имеется произвольных постоянных. В задачах с закрепленными концами для их определения имеется  граничных условий. Таким образом, число неизвестных совпадает с числом уравнений. Однако, возможность разрешимости полученной системы уравнений относительно искомых переменных зависит от формы исходных данных. граничных условий. Таким образом, число неизвестных совпадает с числом уравнений. Однако, возможность разрешимости полученной системы уравнений относительно искомых переменных зависит от формы исходных данных.
Теперь рассмотрим необходимые условия для задачи оптимизации со свободным правым концом (значение  не задано). В такой постановке допускается вариация значения не задано). В такой постановке допускается вариация значения 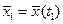 , и поэтому первая вариация функционала может быть представлена в виде: , и поэтому первая вариация функционала может быть представлена в виде:
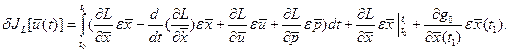
Необходимое условие экстремума 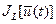 согласно необходимому условию экстремума функционала (1.17) в этом случае содержит уравнения равенства в виде (1.28), а также следующие соотношения: согласно необходимому условию экстремума функционала (1.17) в этом случае содержит уравнения равенства в виде (1.28), а также следующие соотношения:
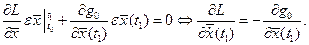 (1.30) (1.30)
Уравнение (1.30) называется условиями трансверсальности для свободного правого конца траектории. Подобное соотношение может быть написано для левого конца траектории, если он не закреплен. Условия трансверсальности восполняют недостаток информации за счет потери граничных условий при свободных концах траектории.
Для решения многих задач более удобной является другая форма представления системы (1.28), которая называется канонической. Определим скалярную функцию – гамильтониан:
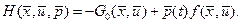
В отличие от лагранжиана 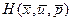 не содержит слагаемого не содержит слагаемого 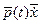 , поэтому , поэтому

Отсюда
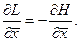
Каноническая форма системы (1.28) имеет вид:
 , , 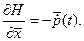 (1.31) (1.31)
Очевидно, система (1.31) содержащая два векторных уравнения, эквивалентна двум уравнениям системы (1.28) Далее рассмотрим применение полученных теоретических положений для решения практических задач.
Пример 1. Требуется определить оптимальную траекторию движения объекта при следующих исходных данных [6]:
описание движения объекта 
краевые условия  , , 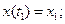
критерий оптимизации 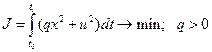
Для решения задачи составим лагранжиан:
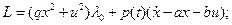
причем  и выпишем необходимые условия экстремума функционала: и выпишем необходимые условия экстремума функционала:
стационарность по 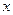 : :
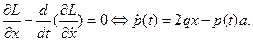
стационарность по 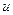 : :
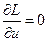 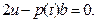
Полученные уравнения позволяют выразить функцию управления 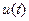 через через 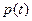 и исключить затем ее из уравнения связи: и исключить затем ее из уравнения связи:

Из последнего уравнения выразим множитель  , затем продифференцируем его по времени и подставим , затем продифференцируем его по времени и подставим  , , 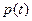 в уравнение стационарности по в уравнение стационарности по 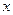 : :
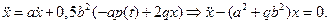
Решение этого уравнения:
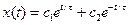 , , 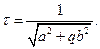
Неизвестные коэффициенты можно определить из краевых условий:
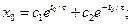
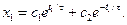
Пример 2. Задача синтеза оптимального регулятора [5]. Требуется определить структуру регулятора, который обеспечивал бы оптимальный режим движения объекта, передаточная функция которого имеет вид колебательного звена:

В пространстве состояний динамика колебательного звена описывается системой уравнений:
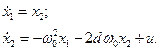
Рассматривается режим отработки ненулевых начальных условий, что соответствует задаче с закрепленными концами:
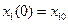 , , 
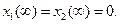
Критерий оптимизации имеет вид:

где 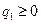 , ,  , ,  - некоторые весовые коэффициенты. Для решения задачи синтеза регулятора нужно найти уравнение, связывающее управляющий сигнал - некоторые весовые коэффициенты. Для решения задачи синтеза регулятора нужно найти уравнение, связывающее управляющий сигнал 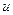 и переменные состояния и переменные состояния 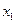 и и  . Для решения задачи формируется лагранжиан при . Для решения задачи формируется лагранжиан при  : :
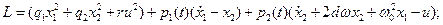
Система уравнений Эйлера-Лагранжа имеет вид:
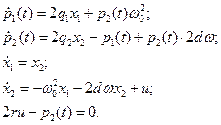
Из последнего уравнения системы можно выразить управляющее воздействие:

и, подставив во второе уравнение связи, получим систему уравнений:

Характеристическое уравнение этой системы:
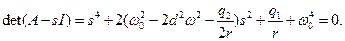
Обозначим 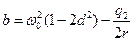 , , 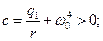
Тогда расположение корней характеристического уравнения на комплексной плоскости будет определяться соотношением между  и и  . При . При  и и  все корни характеристического уравнения чисто мнимые и оптимального все корни характеристического уравнения чисто мнимые и оптимального
|



 ) функции многих переменных
) функции многих переменных 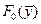
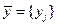
 принято называть экстремальными. При этом возможны два варианта постановки задачи. Допустимая область существования
принято называть экстремальными. При этом возможны два варианта постановки задачи. Допустимая область существования 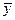 , в которой ищется
, в которой ищется  , обеспечивающий
, обеспечивающий 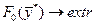 не ограничена. Такие задачи называются задачами на безусловный экстремум. Согласно определению функция
не ограничена. Такие задачи называются задачами на безусловный экстремум. Согласно определению функция 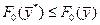
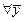 (минимум)
(минимум) 
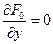 при
при 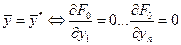 при
при 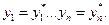 (1.2)
(1.2)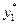 значения
значения 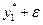 , значение функции
, значение функции 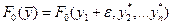 описывается соотношением
описывается соотношением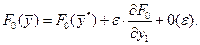 (1.3)
(1.3)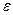 достаточно малым и придавая ему произвольный знак, всегда можно добиться того, чтобы условие (1.1) было нарушено, если не выполнено условие (1.2), что противоречит прямому допущению. Точки
достаточно малым и придавая ему произвольный знак, всегда можно добиться того, чтобы условие (1.1) было нарушено, если не выполнено условие (1.2), что противоречит прямому допущению. Точки 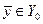 и
и 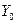 , то условие (1.2) не является необходимым. Например, пусть допустимыми являются только значения
, то условие (1.2) не является необходимым. Например, пусть допустимыми являются только значения  и точка
и точка 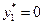 . Тогда в этой точке может достигаться минимум, если даже
. Тогда в этой точке может достигаться минимум, если даже 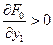 , что также прямо следует из (1.3), поскольку в этой формуле можно выбирать только
, что также прямо следует из (1.3), поскольку в этой формуле можно выбирать только 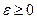 . Как правило, допустимая область
. Как правило, допустимая область 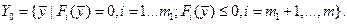 (1.4)
(1.4)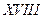 веке был предложен метод, который получил название «метод множителей Лагранжа».
веке был предложен метод, который получил название «метод множителей Лагранжа». , требуется определить
, требуется определить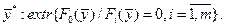 (1.5)
(1.5)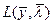 как сумма экстремизируемой функции
как сумма экстремизируемой функции 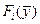 умноженных на множители Лагранжа
умноженных на множители Лагранжа 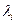 ,
, 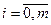 :
: (1.6)
(1.6)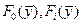
 непрерывно дифференцируемы в окрестности точки
непрерывно дифференцируемы в окрестности точки 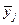 .
. при
при 

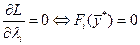
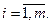
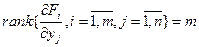 , то заведомо существуют такие
, то заведомо существуют такие  [2]. Нужно заметить, что множители Лагранжа определены с точностью до пропорциональности. Если известно, что
[2]. Нужно заметить, что множители Лагранжа определены с точностью до пропорциональности. Если известно, что  . Тогда число уравнений (1.7) сравняется с числом неизвестных. Согласно содержанию метода Лагранжа, точки
. Тогда число уравнений (1.7) сравняется с числом неизвестных. Согласно содержанию метода Лагранжа, точки  являются подозрительными на экстремум. Для того, чтобы выяснить, будет ли в этих точках в действительности реализовываться локальный минимум, максимум или точка перегиба, нужно провести дополнительные исследования либо путем привлечения вторых производных функций Лагранжа по переменной
являются подозрительными на экстремум. Для того, чтобы выяснить, будет ли в этих точках в действительности реализовываться локальный минимум, максимум или точка перегиба, нужно провести дополнительные исследования либо путем привлечения вторых производных функций Лагранжа по переменной 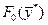 .
.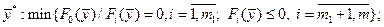 (1.8)
(1.8)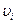
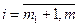 превратим ограничения неравенства в уравнения:
превратим ограничения неравенства в уравнения: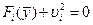
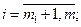 (1.9)
(1.9)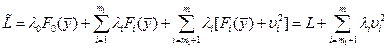 ,
, 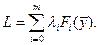 (1.10)
(1.10) , в отличие от
, в отличие от 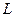 , зависит от переменных
, зависит от переменных 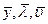 . Необходимые условия безусловного экстремума
. Необходимые условия безусловного экстремума 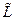 состоят из следующих уравнений:
состоят из следующих уравнений: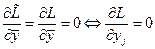 ,
,  (1.11)
(1.11)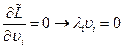 ,
, 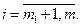 (1.12)
(1.12)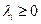 ,
,  (всегда положительного слагаемого) и при решении задачи на минимум функции
(всегда положительного слагаемого) и при решении задачи на минимум функции 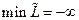 . Условия (1.12) означают, что в точке минимума либо
. Условия (1.12) означают, что в точке минимума либо 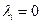 , либо
, либо 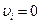 , т.е. с учетом (1.9):
, т.е. с учетом (1.9):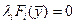 ,
,  , необходимо, чтобы существовали числовые множители
, необходимо, чтобы существовали числовые множители 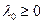 , не равные одновременно нулю, и такие, чтобы они совместно с
, не равные одновременно нулю, и такие, чтобы они совместно с 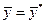 удовлетворяет системе условий:
удовлетворяет системе условий: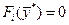

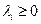
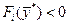 , то указанный набор множителей
, то указанный набор множителей 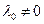 , так что функция Лагранжа может быть записана с
, так что функция Лагранжа может быть записана с  .
.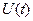 из множества
из множества 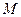 поставлено в соответствие по некоторому правилу число
поставлено в соответствие по некоторому правилу число  , то говорят, что на множестве
, то говорят, что на множестве 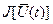 . Множество
. Множество  (класс функций
(класс функций 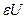 аргумента
аргумента  называется разность между двумя функциями
называется разность между двумя функциями  из выбранного множества
из выбранного множества 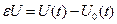 ,
, 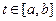 .
.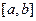 , близки в смысле близости нулевого порядка, если модуль разности
, близки в смысле близости нулевого порядка, если модуль разности 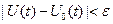 для
для  при
при 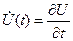 ), то кривые близки в смысле близости первого порядка. Геометрически это означает, что кривые при
), то кривые близки в смысле близости первого порядка. Геометрически это означает, что кривые при  близки в смысле близости
близки в смысле близости 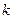 -го порядка, если выполняются неравенства:
-го порядка, если выполняются неравенства: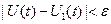 ,
,  ,…
,… 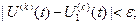
 в смысле близости
в смысле близости 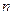 -го порядка, если для любого числа
-го порядка, если для любого числа 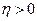 существует число
существует число 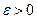 , такое, что для всех допустимых функций
, такое, что для всех допустимых функций  ,…
,… 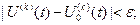
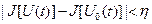 . Функционал, не являющийся непрерывным смысле близости
. Функционал, не являющийся непрерывным смысле близости 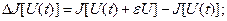

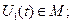

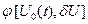 , что для любого допустимого приращения
, что для любого допустимого приращения  функции
функции 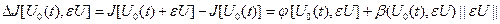

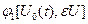 называется сильным дифференциалом (дифференциал Фреше) функционала
называется сильным дифференциалом (дифференциал Фреше) функционала 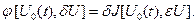 (1.16)
(1.16)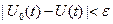 ,
, 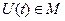 разность
разность  сохранят знак, то функционал
сохранят знак, то функционал 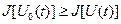 выполняется для всех кривых функционального пространства
выполняется для всех кривых функционального пространства 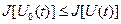 для всех кривых
для всех кривых 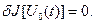 (1.17)
(1.17)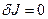 , называют стационарными функциями или стационарными точками функционального пространства задания функционала [4].
, называют стационарными функциями или стационарными точками функционального пространства задания функционала [4].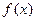 , заданная на отрезке
, заданная на отрезке 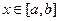 , непрерывна и для любой непрерывной функции
, непрерывна и для любой непрерывной функции  , заданной на отрезке
, заданной на отрезке 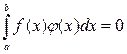 , то
, то 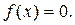
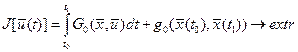
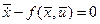 ;
; 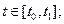 (1.18)
(1.18)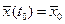 ,
,  .
.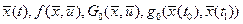 являются непрерывными и дифференцируемыми (принадлежат пространству
являются непрерывными и дифференцируемыми (принадлежат пространству 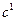 ), функция
), функция 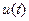 - непрерывная (принадлежит пространству
- непрерывная (принадлежит пространству 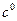 ). Постановка задачи оптимизации:
). Постановка задачи оптимизации: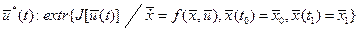 ,
, 
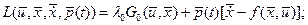 (1.19)
(1.19)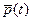 - непрерывная вектор-функция множителей Лагранжа.
- непрерывная вектор-функция множителей Лагранжа. , что фактически означает наличие бесконечного числа ограничений, числовые множители Лагранжа представляются функцией времени.
, что фактически означает наличие бесконечного числа ограничений, числовые множители Лагранжа представляются функцией времени. переходим к задаче:
переходим к задаче: (1.20)
(1.20)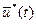 найдено. Следовательно, определена оптимальная траектория САУ
найдено. Следовательно, определена оптимальная траектория САУ 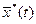 , на которой функционал (1.20) достигает экстремума. Рассмотрим его приращение за счет малой
, на которой функционал (1.20) достигает экстремума. Рассмотрим его приращение за счет малой  - вариации оптимального уравнения и соответствующей ей вариации траектории системы
- вариации оптимального уравнения и соответствующей ей вариации траектории системы 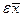 . Так как функции
. Так как функции  и
и  являются гладкими, малые вариации управления дают и малые вариации значения функционала
являются гладкими, малые вариации управления дают и малые вариации значения функционала 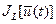 . Допустим, что функция
. Допустим, что функция 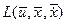 непрерывна по совокупности своих аргументов и имеет непрерывные частные производные второго порядка по всем аргументам в области
непрерывна по совокупности своих аргументов и имеет непрерывные частные производные второго порядка по всем аргументам в области  ,
, 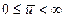 ,
, 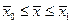 ,
, 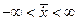 . Приращение функционала
. Приращение функционала 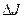 , отвечающее приращению
, отвечающее приращению  имеет вид
имеет вид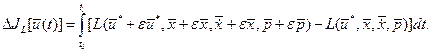 (1.21)
(1.21)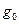 ) отсутствует в выражении (1.21). Представим разность функций под интегралом (1.21) в виде разложения Тейлора, что допустимо вследствие непрерывности функции
) отсутствует в выражении (1.21). Представим разность функций под интегралом (1.21) в виде разложения Тейлора, что допустимо вследствие непрерывности функции 
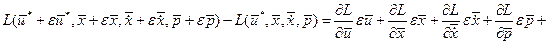
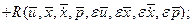
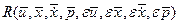 - остаточный член разложения ряда Тейлора. После подстановки (1.22) в (1.21) получим
- остаточный член разложения ряда Тейлора. После подстановки (1.22) в (1.21) получим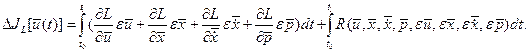 (1.23)
(1.23) и
и 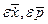 . Пусть все вторые частные производные функции
. Пусть все вторые частные производные функции  по
по 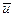 ,
, 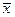 ,
,  и
и 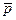 не превосходит по абсолютной величине некоторой константы
не превосходит по абсолютной величине некоторой константы 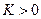 . Выберем
. Выберем  таким образом, чтобы была справедлива оценка:
таким образом, чтобы была справедлива оценка: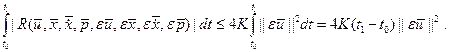 (1.24)
(1.24)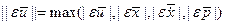 . Следовательно, второе слагаемое в правой части (1.22) – второго порядка малости относительно
. Следовательно, второе слагаемое в правой части (1.22) – второго порядка малости относительно  и согласно определению функционал
и согласно определению функционал  является дифференцируемым в пространстве
является дифференцируемым в пространстве  и его первая вариация имеет вид:
и его первая вариация имеет вид: (1.25)
(1.25)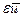 ,
, 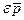 - векторы вариации траектории, управления и множителей Лагранжа соответственно. В результат интегрирования по частям третьего слагаемого в (1.25) имеем:
- векторы вариации траектории, управления и множителей Лагранжа соответственно. В результат интегрирования по частям третьего слагаемого в (1.25) имеем: (1.26)
(1.26) закреплены, и вариация траектории на концах исключается
закреплены, и вариация траектории на концах исключается 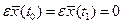 . С учетом (1.25) и (1.26) необходимое условие экстремума функционала (1.20) имеет вид:
. С учетом (1.25) и (1.26) необходимое условие экстремума функционала (1.20) имеет вид: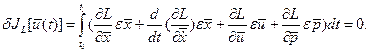 (1.27)
(1.27)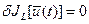 может быть выполнено, если интеграл от каждого слагаемого равен нулю. Тогда согласно основной лемме вариационного исчисления можно записать:
может быть выполнено, если интеграл от каждого слагаемого равен нулю. Тогда согласно основной лемме вариационного исчисления можно записать: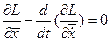 ,
,  ,
,  (1.28)
(1.28)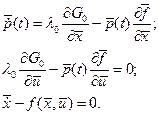 (1.29)
(1.29)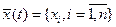 ,
,  ,
,  . Всего неизвестных функций
. Всего неизвестных функций  ,для их определения имеется
,для их определения имеется 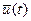 через
через  скалярных дифференциальных уравнений. Ее решение зависит от
скалярных дифференциальных уравнений. Ее решение зависит от  не задано). В такой постановке допускается вариация значения
не задано). В такой постановке допускается вариация значения 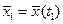 , и поэтому первая вариация функционала может быть представлена в виде:
, и поэтому первая вариация функционала может быть представлена в виде: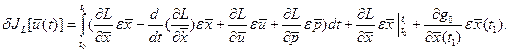
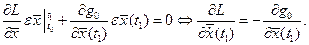 (1.30)
(1.30)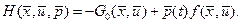
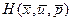 не содержит слагаемого
не содержит слагаемого 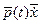 , поэтому
, поэтому
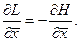
 ,
, 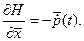 (1.31)
(1.31)
 ,
, 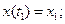
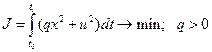
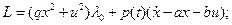
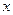 :
: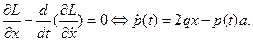
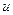 :
: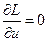
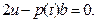
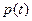 и исключить затем ее из уравнения связи:
и исключить затем ее из уравнения связи:
 , затем продифференцируем его по времени и подставим
, затем продифференцируем его по времени и подставим  ,
, 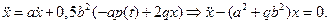
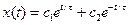 ,
, 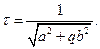
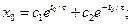
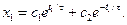

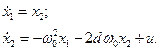
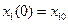 ,
, 
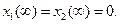

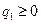 ,
,  ,
,  - некоторые весовые коэффициенты. Для решения задачи синтеза регулятора нужно найти уравнение, связывающее управляющий сигнал
- некоторые весовые коэффициенты. Для решения задачи синтеза регулятора нужно найти уравнение, связывающее управляющий сигнал 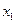 и
и  . Для решения задачи формируется лагранжиан при
. Для решения задачи формируется лагранжиан при 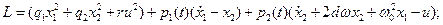
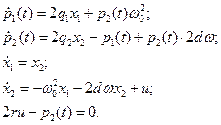


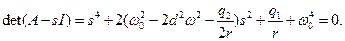
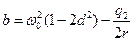 ,
, 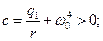
 и
и  . При
. При  и
и  все корни характеристического уравнения чисто мнимые и оптимального
все корни характеристического уравнения чисто мнимые и оптимального 


