
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимые условия оптимальности для непрерывных систем
Как уже отмечалось ранее, на основании сформулированного принципа оптимальности Беллманом были получены условия, которым должно удовлетворять оптимальное управление для непрерывных динамических систем. В общем случае описание динамической системы представляется в форме описания в переменных состояния:
где
Величина управляющего воздействия имеет ограничения, определяемые характером и возможностями объекта. Это означает, что вектор управления
Допустим, что найдена оптимальная траектория
Представим выражение (3.11) в виде двух слагаемых согласно разбиению траектории:
Если принять, что
где
Выражение (3.13) является исходным для вывода уравнения Беллмана, содержащего необходимые условия для решения задач оптимизации непрерывных процессов. Однако вывод уравнения требует непрерывности функции
Допустим, что потенциал
В выражении (3.14) исключаем
Согласно выражению (3.11) краевое условие для правого конца траектории имеет вид:
При организации решения уравнения (3.15) необходимо, прежде всего провести операцию минимизации правой части по
Допустим, что уравнение (3.16) позволяет определить
Выражения (3.17) и (3.16) представляют собой необходимые условия оптимальности для определения
здесь сомножитель
Первое уравнение в системе (3.19) очевидно, обоснованием второго уравнения могут служить следующие соотношения:
Дифференцируя уравнение (3.17) по
Градиент потенциала называют также сопряженным состоянием, так как по форме уравнения для него имеют характер сопряженных уравнениям состояния, как видно из (3.19). В задаче без ограничений система (3.19) эквивалентна уравнениям (1.31), при этом вектор
где по-прежнему
Рассмотрим задачу с закрепленными концами, когда
Пусть
Разобьем оптимальную траекторию от
Тогда по аналогии с рассмотренным выше выражение для
В связи с тем, что рассматривается стационарный случай, функции
где через
Это есть уравнение Беллмана для стационарной задачи с фиксированными границами и свободным временем перехода. При рассмотрении задачи оптимальности по быстродействию подинтегральная функция функционала
Если решается задача быстродействия при условии
Теперь рассмотрим несколько примеров.
Пример I. Задача оптимального управления для линейной стационарной САУ при произвольном критерии не зависящем от управления
Описание САУ в пространстве состояний:
Ограничение на управление
Определяем уравнение Беллмана:
Проведение операции минимизации в представленном уравнении позволяет записать выражения для оптимальных значений составляющих вектора управления:
Для САУ
Необходимые функции
Пример II. Описание объекта управления [10]
Ограничение на управляющее воздействие
Оптимальное управляющее воздействие задается соотношением:
На основании описания объекта
Пример III. Исходные данные:
Требуется определить управляющее воздействие, минимизирующее функционал
На основании процедуры минимизации можно получить аналитическое выражение для определения оптимального управления без учета ограничения на
С учетом ограничений
Функции
и граничных условий.
Пример IV. Определить оптимальное управление с обратной связью в следующей задаче [9]:
Для решения задачи запишем уравнение Беллмана
Проводим операцию минимизации и определяем оптимальное управляющее воздействие:
Подставляем
Нужно решить это уравнение при граничном условии Будем искать решение в виде квадратичной формы
Которая удовлетворяет указанному граничному условию. Подставив это выражение в уравнение Беллмана, получим
Или
Последнее равенство будет выполняться тождественно, если
Эта система имеет следующее решение:
Из исходных данных
Последнее равенство представляет собой уравнение регулятора.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.189.177 (0.078 с.) |

 -мерный вектор координат состояния;
-мерный вектор координат состояния; -мерный вектор управления.
-мерный вектор управления.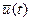 принимает значения из некоторой области пространства управления
принимает значения из некоторой области пространства управления  . Задача оптимизации управления состоит в том, чтобы определить управляющее воздействие
. Задача оптимизации управления состоит в том, чтобы определить управляющее воздействие  , которое переводит объект из начального состояния
, которое переводит объект из начального состояния  в точку
в точку  , и минимизирует критерий оптимизации в виде функционала:
, и минимизирует критерий оптимизации в виде функционала:
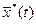 , выходящая из начальной точки
, выходящая из начальной точки  и проходящая через точку
и проходящая через точку  . Рассмотрим на траектории промежуточные точки
. Рассмотрим на траектории промежуточные точки  и
и  (рис. 3.7), соответствующие моменту времени
(рис. 3.7), соответствующие моменту времени  и
и  . Обозначим минимальное значение функционала через
. Обозначим минимальное значение функционала через  , где по аналогии с дискретным случаем
, где по аналогии с дискретным случаем  также является оптимальной траекторией и значение потенциала равно
также является оптимальной траекторией и значение потенциала равно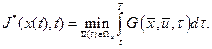 (3.11)
(3.11) (3.12)
(3.12) - мало, первое слагаемое можно определить
- мало, первое слагаемое можно определить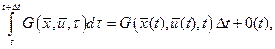
 малая величина, более высокого порядка малости, чем
малая величина, более высокого порядка малости, чем  можно записать в виде:
можно записать в виде: (3.13)
(3.13) является гладкой функцией состояния и представим в виде ряда Тейлора:
является гладкой функцией состояния и представим в виде ряда Тейлора: (3.14)
(3.14) , делим все слагаемые на
, делим все слагаемые на  и переносим производную потенциала по времени влево. В итоге получаем дифференциальное уравнение, разрешенное относительно производной потенциала по времени, которое называется уравнением Беллмана:
и переносим производную потенциала по времени влево. В итоге получаем дифференциальное уравнение, разрешенное относительно производной потенциала по времени, которое называется уравнением Беллмана: (3.15)
(3.15)
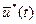 лежит внутри области допустимых значений
лежит внутри области допустимых значений 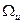 , то можно использовать необходимые условия стационарности по
, то можно использовать необходимые условия стационарности по  (3.16)
(3.16)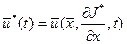 , тогда найденное
, тогда найденное  . Полученное уравнение называется уравнением Гамильтона-Якоби и имеет вид:
. Полученное уравнение называется уравнением Гамильтона-Якоби и имеет вид: (3.17)
(3.17) и
и  . Уравнение (3.17), как правило, является нелинейным и аналитическое решение системы (3.17). (3.16) возможно только в простейших случаях. Кроме того, если
. Уравнение (3.17), как правило, является нелинейным и аналитическое решение системы (3.17). (3.16) возможно только в простейших случаях. Кроме того, если 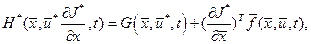 (3.18)
(3.18) в соответствии со своей формой называется градиентом потенциала. В последующем тексте обозначим
в соответствии со своей формой называется градиентом потенциала. В последующем тексте обозначим  . На основании выражения (3.18) можно от одного скалярного уравнения (3.17) перейти к двум векторным (или
. На основании выражения (3.18) можно от одного скалярного уравнения (3.17) перейти к двум векторным (или  скалярным) обыкновенным дифференциальным уравнениям Гамильтона относительно состояния и градиента потенциала:
скалярным) обыкновенным дифференциальным уравнениям Гамильтона относительно состояния и градиента потенциала: (3.19)
(3.19) (3.20)
(3.20)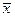 , имеем:
, имеем: (3.21)
(3.21) совпадает с вектором множителей Лагранжа
совпадает с вектором множителей Лагранжа 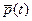 . В [11] показано, что уравнения (3.19) остаются справедливыми и в случае, если условия гладкости функции
. В [11] показано, что уравнения (3.19) остаются справедливыми и в случае, если условия гладкости функции 
 . В этом случае подинтегральная функция минимизируемого функционала также не зависит явно от
. В этом случае подинтегральная функция минимизируемого функционала также не зависит явно от 
 из начального состояния в конечное не фиксируется. Если найдено оптимальное управление
из начального состояния в конечное не фиксируется. Если найдено оптимальное управление 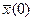 .
.

 справа от
справа от 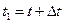 , где
, где 
 можно записать в виде двух слагаемых:
можно записать в виде двух слагаемых: (3.22)
(3.22) и
и  не зависят явно от временили, и разложение функции
не зависят явно от временили, и разложение функции  в ряд Тейлора имеет вид:
в ряд Тейлора имеет вид: (3.23)
(3.23)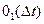 обозначены члены разложения, имеющие более высокий порядок малости, чем
обозначены члены разложения, имеющие более высокий порядок малости, чем  (3.24)
(3.24) и уравнение Беллмана имеет вид:
и уравнение Беллмана имеет вид: (3.25)
(3.25) (перевод объекта из состояния
(перевод объекта из состояния  уравнения (3.29) должно удовлетворять граничному условию
уравнения (3.29) должно удовлетворять граничному условию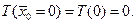
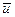 :
:

 . Составляющие вектора градиента потенциала:
. Составляющие вектора градиента потенциала: .
.

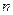 -го порядка оптимальное управление для составляющей
-го порядка оптимальное управление для составляющей  вектора
вектора 
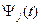 определяются из решения системы уравнений (3.14) для конкретного математического описания САУ.
определяются из решения системы уравнений (3.14) для конкретного математического описания САУ.
 , критерий оптимизации
, критерий оптимизации  . Уравнение Беллмана для данной задачи:
. Уравнение Беллмана для данной задачи:

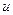 функции
функции  определяется из системы уравнений:
определяется из системы уравнений:
 ,
,  ,
,  ,
,  . Составляем уравнение Беллмана:
. Составляем уравнение Беллмана: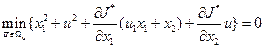

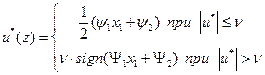
 ,
, 





 в уравнение Беллмана, в котором отсутствует операция минимизации:
в уравнение Беллмана, в котором отсутствует операция минимизации:
 .
. ,
,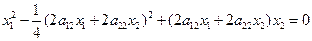



 при всех
при всех  , т.е.
, т.е.  - положительно определенная функция, поэтому в качестве решения следует рассматривать
- положительно определенная функция, поэтому в качестве решения следует рассматривать . Тогда выражение для определения значения критерия оптимизации и оптимального управления имеют вид
. Тогда выражение для определения значения критерия оптимизации и оптимального управления имеют вид




