
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача быстродействия для траектории с закреплёнными концами.Содержание книги
Поиск на нашем сайте
Во многих задачах автоматического управления возникает необходимость минимизации времени перехода объекта из начального состояния в конечное. Такие оптимизационные задачи называются задачами быстродействия. Важность и распространённость задач быстродействия позволяют уделить им особое внимание и отдельно сформулировать теорему принципа максимума. Критерий оптимизации в этом случае имеет вид:
и, следовательно, интегрант
Соотношения (2.11) для гамильтониана (2.19) остаются справедливыми. Тогда основная теорема принципа максимума для оптимальности по быстродействию и задачи с закрепленными концами формулируется следующим образом[8][10]. Теорема. Пусть 1) для любого
2) в конечный момент времени
В рассматриваемой задаче быстродействия интегрант
где В – матрица числовых коэффициентов, оптимальное управляющее воздействие имеет вид кусочно-постоянной функции с конечным числом интервалов переключения. Функция гамильтониан в этом случае имеет вид:
Управляющее воздействие содержится только во втором слагаемом и, следовательно, максимальное значение
Из выражения (2.22) следует, что для всех
где A и B – матрицы с постоянными коэффициентами. Тогда теорема об Теорема. Если характеристические числа матрицы A – действительные числа и область управления Гамильтониан для объекта управления
Так как от управлений
Это условие выполняется, если каждое слагаемое по индексу j примет максимальное значение по модулю и со знаком, определяемым знаком суммы составляющих
Для определения моментов смены знака для
Система уравнений (2.25) является сопряженной относительно (2.23) при
Корни характеристического уравнения (2.25) равны корням характеристического уравнения (2.26) и имеют противоположный знак. Согласно теореме, корни (2.26) действительные и отрицательные
И оптимальное значение составляющих управления:
Функция, представляющая собой сумму экспонент с постоянными коэффициентами на полубесконечном интервале Пример 1. Задача об оптимальной по быстродействию встрече движущихся объектов.[5] Объект A движется равномерно и прямолинейно. Изменение его координаты
По той же прямой в пространстве за ним движется объект B, изменение координаты
Управление имеет ограничение На практике подобная задача возникает, например, при заправке в воздухе самолетов, когда заправщик движется с постоянной скоростью и на параллельный курс к нему пристраивается заправляемый самолет. Управляющим воздействием при этом является тяга p двигателя самолета, заходящего на заправку. Предельные значения тяги
Решение задачи удобнее провести относительно рассогласования между координатами объектов:
Относительно x процесс сближения двух объектов описывается уравнением:
Начальные условия для x:
В задачах быстродействия критерий оптимизации имеет вид:
Для решения задачи принципом максимума представим описание процесса сближения в форме пространства состояний:
Составим гамильтониан:
В выражении для
Уравнение для вектора
На основании выражения для
При всех возможных сочетаниях знаков
Система уравнений связи (1П) решается последовательно для
На втором этапе начальные значения
Из двух последних уравнений можно получить два соотношения для определения
Пример 2. Требуется определить экстремаль, которая минимизирует функционал
При условиях: Имеем задачу с одним закрепленным концом и заданным временем движения объекта. В связи с тем, что имеется ограничение на скорость, задачу нельзя решить методом вариационного исчисления. Для решения на основе принципа максимума приведем задачу к виду задач оптимального управления:
Составим функцию Лагранжа и гамильтониан
Условие стационарности по x (уравнение сопряженного состояния) имеет вид:
Условие трансверсальности:
Если
Определяем уравнение для сопряженного состояния
Оптимальная траектория определяется из уравнения связи:
Постоянные
|
||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 486; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.127.131 (0.006 с.) |

 (2.18)
(2.18) . При описании объекта в виде (2.1) функция гамильтониан формируется:
. При описании объекта в виде (2.1) функция гамильтониан формируется: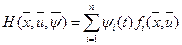 (2.19)
(2.19) - некоторое допустимое управление, переводящее объект из состояния
- некоторое допустимое управление, переводящее объект из состояния  , в состояние
, в состояние  , а
, а 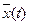 - соответствующая этому управлению фазовая траектория. Для оптимальности по быстродействию управления
- соответствующая этому управлению фазовая траектория. Для оптимальности по быстродействию управления  и траектории
и траектории  необходимо существование такой ненулевой непрерывной вектор - функции
необходимо существование такой ненулевой непрерывной вектор - функции  , удовлетворяющей системе уравнений (2.7), что:
, удовлетворяющей системе уравнений (2.7), что: , являющегося точкой непрерывности управления
, являющегося точкой непрерывности управления  , функция
, функция 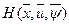 достигнет по
достигнет по  (2.20)
(2.20)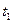 выполняется соотношение:
выполняется соотношение: (2.21).
(2.21). не содержит в качестве переменной управляющее воздействие
не содержит в качестве переменной управляющее воздействие  . Это обстоятельство позволяет сделать очень важный вывод. Если в
. Это обстоятельство позволяет сделать очень важный вывод. Если в  ,
,
 . Если множество
. Если множество 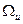 – замкнутое, ограничение на составляющие вектора
– замкнутое, ограничение на составляющие вектора  , и оптимальное значение
, и оптимальное значение (2.22)
(2.22) по модулю равно максимально допустимому значению
по модулю равно максимально допустимому значению 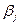 , а по знаку зависит от знака суммы составляющих вектора
, а по знаку зависит от знака суммы составляющих вектора  . Число переключений для
. Число переключений для  определяется числом переменных состояния или (что равно) степенью дифференциального уравнения, описывающего динамику объекта оптимизации. Этот факт утверждается теоремой об
определяется числом переменных состояния или (что равно) степенью дифференциального уравнения, описывающего динамику объекта оптимизации. Этот факт утверждается теоремой об 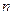 – интервалах[8]. Пусть описание динамических свойств объекта имеет вид:
– интервалах[8]. Пусть описание динамических свойств объекта имеет вид: (2.23)
(2.23) является кусочно-постоянной функцией и имеет не более n-1 переключении (т.е. не более n интервалов постоянства), где n – порядок системы.
является кусочно-постоянной функцией и имеет не более n-1 переключении (т.е. не более n интервалов постоянства), где n – порядок системы. (2.23)
(2.23)
 необходимо знать функции
необходимо знать функции 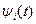 , которые для объекта управления с описанием (2.23) имеют математическое представление согласно (2.7)
, которые для объекта управления с описанием (2.23) имеют математическое представление согласно (2.7) (2.25)
(2.25) (свободное движение):
(свободное движение):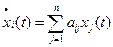 (2.26)
(2.26) , тогда
, тогда
 (2.27)
(2.27) , может переходить через ноль не более (n-1) раз и имеет, следовательно, не более n интервалов постоянства. При комплексных корнях характеристического уравнения системы (2.26) число интервалов постоянства может быть больше и зависит от начальных условий системы (2.22).
, может переходить через ноль не более (n-1) раз и имеет, следовательно, не более n интервалов постоянства. При комплексных корнях характеристического уравнения системы (2.26) число интервалов постоянства может быть больше и зависит от начальных условий системы (2.22). соответствует уравнению:
соответствует уравнению:
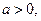

 которого описывается уравнением второго порядка:
которого описывается уравнением второго порядка: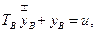


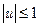 . Требуется определить такое управление
. Требуется определить такое управление 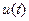 , чтобы за минимальное время положение и скорости объектов A и B в пространстве совпали.
, чтобы за минимальное время положение и скорости объектов A и B в пространстве совпали. и
и  положительны. Для того чтобы записать ограничение на управление
положительны. Для того чтобы записать ограничение на управление 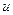 в принятом выше виде, его значение через
в принятом выше виде, его значение через  представляется следующим образом:
представляется следующим образом: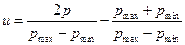
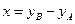





 (1П)
(1П)
 от управления зависит только последнее слагаемое, поэтому максимальное значение
от управления зависит только последнее слагаемое, поэтому максимальное значение 

 можно записать закон оптимального управления
можно записать закон оптимального управления
 и
и  функция
функция 
 , а на втором
, а на втором 
 . Момент переключения
. Момент переключения  составляют неизвестные параметры. Для их определения используем граничные условия и физические особенности протекания процесса движения. Так для
составляют неизвестные параметры. Для их определения используем граничные условия и физические особенности протекания процесса движения. Так для  согласно условию задачи движения объектов характеризуется тем, что
согласно условию задачи движения объектов характеризуется тем, что  и
и  , что позволяет определить граничные условия для
, что позволяет определить граничные условия для 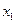 и
и  в момент времени
в момент времени  и
и 



 и
и  определяются как результат движения объектов на первом этапе, что позволяет найти постоянные интегрирования и определить
определяются как результат движения объектов на первом этапе, что позволяет найти постоянные интегрирования и определить  и
и  , приравняв их к нулю:
, приравняв их к нулю:

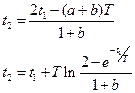



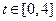

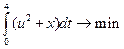


 Условие оптимальности по управлению:
Условие оптимальности по управлению:


 , то
, то 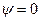 , что недопустимо. Принимаем
, что недопустимо. Принимаем  , тогда оптимальное управление
, тогда оптимальное управление  с учетом ограничения имеет вид:
с учетом ограничения имеет вид:






