
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача с закрепленными концами и фиксированным временем.
В начале рассмотрим условия принципа максимума для задачи с закрепленными концами. Описание объекта имеет вид:
Вектор управления
Где
Согласно исходным данным задачи выражение (2.3) для
Результат решения задачи (2.4) предполагает определение оптимальных функций
При решении (2.5) и (2.6) предполагается рассматривать класс допустимых функций
Условие (2.7) называется сопряженной системой, решение которой позволяет определить вектор Очевидно решение второй задачи (2.6). Оптимальное управление
Введение гамильтониана
Условием максимизации
Следовательно Теорема(принцип максимума) Пусть
Согласно теореме в формулировке принципа максимума имеются Если точка
Если же некоторые составляющие вектор – функции На основании введенной функции гамильтониана необходимое условие (2.7), (2.8) также можно представить в форме канонических уравнений:
|
||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 577; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.250.1 (0.007 с.) |

 (2.1)
(2.1) принимает значения из некоторой замкнутой области
принимает значения из некоторой замкнутой области  и принадлежит классу кусочно-непрерывных функций
и принадлежит классу кусочно-непрерывных функций  . Составляющие вектора
. Составляющие вектора  являются непрерывными и всюду, кроме точек разрыва допустимого управления, имеют непрерывные производные
являются непрерывными и всюду, кроме точек разрыва допустимого управления, имеют непрерывные производные  . Функции
. Функции  непрерывны по всем аргументам и имеют непрерывные частные производные по переменным состояния
непрерывны по всем аргументам и имеют непрерывные частные производные по переменным состояния  . Из всех допустимых управлений
. Из всех допустимых управлений  , переводящих объект из начального состояния
, переводящих объект из начального состояния  в конечное
в конечное  , требуется найти такое управление, которое минимизирует функционал:
, требуется найти такое управление, которое минимизирует функционал: (2.2)
(2.2) непрерывная и дифференцируемая функция. Применяем к задаче (2.1-2.2) прием Лагранжа[2], составляем Лагранжиан
непрерывная и дифференцируемая функция. Применяем к задаче (2.1-2.2) прием Лагранжа[2], составляем Лагранжиан (2.3)
(2.3)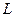 не содержит ограничения на управляющие воздействия, и в соответствии с приемом Лагранжа задача (2.1-2.2) сводится к задаче на безусловный экстремум функционала:
не содержит ограничения на управляющие воздействия, и в соответствии с приемом Лагранжа задача (2.1-2.2) сводится к задаче на безусловный экстремум функционала: (2.4)
(2.4) . Возможность определения этих функций можно представить в форме решения двух задач, в каждой из которых определяется экстремаль по одной переменной при условии, что по другой переменной задача оптимизации решена [2]. Эти задачи имеют вид:
. Возможность определения этих функций можно представить в форме решения двух задач, в каждой из которых определяется экстремаль по одной переменной при условии, что по другой переменной задача оптимизации решена [2]. Эти задачи имеют вид: (2.5)
(2.5)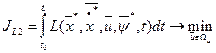 (2.6)
(2.6) в форме
в форме 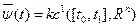 . Задача (2.5) является задачей вариационного исчисления с закрепленными концами на экстремум функционала. Для нее необходимое условие экстремума – уравнение Эйлера:
. Задача (2.5) является задачей вариационного исчисления с закрепленными концами на экстремум функционала. Для нее необходимое условие экстремума – уравнение Эйлера: (2.7)
(2.7) (2.8)
(2.8) множителей Лагранжа.
множителей Лагранжа. , должно удовлетворять условию
, должно удовлетворять условию  . В методе принципа максимума вводится скалярная функция гамильтониан
. В методе принципа максимума вводится скалярная функция гамильтониан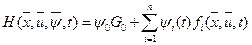 (2.9)
(2.9)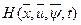 в (2.6) позволяет сформировать эту задачу на максимум функционала при
в (2.6) позволяет сформировать эту задачу на максимум функционала при  :
: (2.10)
(2.10) является максимизация подынтегрального выражения. Функция
является максимизация подынтегрального выражения. Функция  доставляет максимум функционалу
доставляет максимум функционалу  , кроме точек разрыва
, кроме точек разрыва 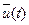 выполняется соотношение:
выполняется соотношение: (2.11)
(2.11) - такое допустимое управление, что соответствующая ему траектория
- такое допустимое управление, что соответствующая ему траектория 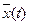 , исходящая при
, исходящая при  из точки
из точки  , проходит в момент
, проходит в момент 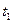 через точку
через точку  . Для оптимальности управления
. Для оптимальности управления  и траектории
и траектории  необходимо существование такой ненулевой непрерывной вектор - функции
необходимо существование такой ненулевой непрерывной вектор - функции  , соответствующей функциям
, соответствующей функциям  и
и  , что для любого момента времени
, что для любого момента времени  достигает по
достигает по 
 неизвестных функций
неизвестных функций  . Совокупность уравнений (2.7), (2.8) и условий (2.11) представляют столько же соотношений для определения этих неизвестных. Постоянные интегрирования определяются на основании граничных условий.
. Совокупность уравнений (2.7), (2.8) и условий (2.11) представляют столько же соотношений для определения этих неизвестных. Постоянные интегрирования определяются на основании граничных условий.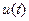 является внутренней точкой области
является внутренней точкой области 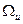 , то для выполнения условия максимума необходимо обращение в нуль
, то для выполнения условия максимума необходимо обращение в нуль  частных производных:
частных производных: . (2.12)
. (2.12) на границе
на границе  ). Управление
). Управление  -подходит к своим граничным значениям в какой-то момент времени
-подходит к своим граничным значениям в какой-то момент времени  , тогда при
, тогда при  -управления
-управления  оптимальное значение
оптимальное значение  при
при  является линейной и однородной функцией переменных
является линейной и однородной функцией переменных  и соотношения (2.7),(2.11) не изменяются при умножении всех переменных на одну и ту же постоянную величину, значение
и соотношения (2.7),(2.11) не изменяются при умножении всех переменных на одну и ту же постоянную величину, значение  , которая согласно теореме является постоянной величиной, можно задаться произвольно. Обычно принимают
, которая согласно теореме является постоянной величиной, можно задаться произвольно. Обычно принимают  .
. ,
,  (2.13)
(2.13)


