
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация задач оптимального управления.
В основу любой классификации выбирается какая – либо существующая характеристика (составляющая) классифицируемой задачи. При решении задачи оптимального управления (ЗОУ) очень важная роль отводится форме критерия оптимизации, который, как правило, задается в виде функционала. Классификация ЗОУ по этому признаку повторяет классификацию экстремальных задач, рассмотренных в вариационном исчислении. Экстремальные задачи иногда называют задачами оптимизации. Задача оптимизации становится задачей оптимального управления, когда среди независимых переменных оптимизируемого функционала появляется управляющее воздействие вектор
1) Интегральный функционал. Задача Лагранжа. Интегральным функционалом называется функционал вида
где 2) Задача Майера. В этом случае минимизируемый функционал является функцией граничных состояний объекта управления:
Функция
3) Задача Больца. Функционал смешанного типа. Определить векторы
Путем введения новой переменной эта задача может быть сведена к задаче Майера.
II Способы задания краевых условий. В общем случае граничные условия (3) можно представить в виде гиперповерхности в пространстве
Однако в конкретных задачах имеются следующие варианты краевых условий. 1) Задача с фиксированными концами. Этот термин используется в задачах, в которых 2) Задача со свободным концом. Если 3) Задача с подвижными концами. Если
III способы задания ограничений.
1) В общем случае ограничение на управление и фазовые координаты имеют вид (2). Однако при решении ЗОУ в технике наиболее часто встречаются ограничения в форме
Классические методы решения ЗОУ, основанные на вариационном исчислении, оказываются неприменимы при наличии ограничений в форме (10). Дл подобных задач в конце 50-х годов был разработан принцип максимума Понтрягина Л.С. 2) Совместные ограничения на управление и фазовые переменные в виде равенств и неравенств:
3) Интегральные ограничения (изопериметрическая задача). Решение ЗОУ определяется при соблюдении ограничения в виде:
где Название этому классу задач дала следующая «историческая» задача, изучавшаяся еще в конце XVIII века: определить форму кривой заданной длины, которая ограничивает максимальную площадь. Приведенная классификация не является всеобъемлющей и не охватывает весь класс задач оптимального управления. Однако она позволяет в дальнейшем использовать терминологию принятую при постановке и решении ЗОУ.
|
||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 760; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.66.13 (0.008 с.) |
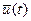 . В классическом вариационном исчислении рассматривались задачи, где переменная
. В классическом вариационном исчислении рассматривались задачи, где переменная  или даже производные более высоких порядков. Очевидно, математическая сущность задачи оптимизации при этом не изменяется, так как переменная
или даже производные более высоких порядков. Очевидно, математическая сущность задачи оптимизации при этом не изменяется, так как переменная 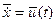 . Далее рассмотрены варианты классификации ЗОУ в зависимости от формы задания функционала (4), ограничений вдоль траектории (2) и краевых условий (3). Основное назначение этой классификации, которая является весьма условной – познакомить читателя с терминологией, которая используется в литературе по данному вопросу [1].
. Далее рассмотрены варианты классификации ЗОУ в зависимости от формы задания функционала (4), ограничений вдоль траектории (2) и краевых условий (3). Основное назначение этой классификации, которая является весьма условной – познакомить читателя с терминологией, которая используется в литературе по данному вопросу [1].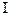 По форме критерия оптимизации.
По форме критерия оптимизации.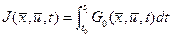 (5)
(5) - является дифференцируемой функцией своих переменных и называется интегрантом. В случае отсутствия ограничений (2) задача о минимуме
- является дифференцируемой функцией своих переменных и называется интегрантом. В случае отсутствия ограничений (2) задача о минимуме 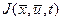 при условиях (1) и (3) традиционно называется задачей Лагранжа. Она является классической задачей вариационного исчисления.
при условиях (1) и (3) традиционно называется задачей Лагранжа. Она является классической задачей вариационного исчисления.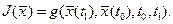 (6)
(6) называется терминантом. Например, для системы (1п) можно поставить следующую задачу Майера: определить управление
называется терминантом. Например, для системы (1п) можно поставить следующую задачу Майера: определить управление  , при котором за заданное время
, при котором за заданное время 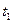 ракета достигает максимальной дальности
ракета достигает максимальной дальности  , при условии, что
, при условии, что 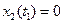 . Формально задача Майера является более общей, чем задача Лагранжа: любая задача Лагранжа может рассматриваться как частный случай задачи Майера.
. Формально задача Майера является более общей, чем задача Лагранжа: любая задача Лагранжа может рассматриваться как частный случай задачи Майера.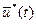 и
и 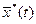 , доставляющие минимум функционалу
, доставляющие минимум функционалу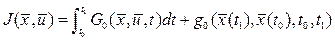 (7)
(7)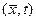 , задаваемые уравнениями
, задаваемые уравнениями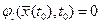 ,
, 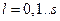 ,
, 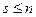 (8)
(8)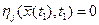 ,
, 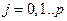 ,
, 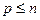 (9)
(9)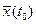 и
и  заданы. Различают также задачи с фиксированным временем (
заданы. Различают также задачи с фиксированным временем (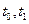 - заданы) и нефиксированным (либо
- заданы) и нефиксированным (либо 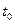 , либо
, либо  ,
, 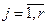
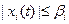 ,
, 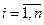 (10)
(10)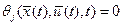 ,
, 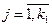 ,
, 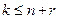
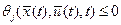 ,
, 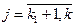 ,
, 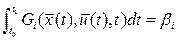 ,
, 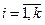
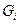 - некоторые скалярные функции, а
- некоторые скалярные функции, а 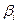 - заданные числа.
- заданные числа.


