
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип оптимальности БеллманаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В середине 50-х годов американский ученый Р.Беллман сформулировал принцип оптимальности, на основе которого были разработаны алгоритмы оптимизации дискретных многошаговых процессов. Позднее принцип был распространен на непрерывные процессы: получены условия, которым должно удовлетворять оптимальное решение. Пусть имеется некоторая физическая система, которая характеризуется
-графом переходов; -таблицей. Примером многошагового процесса может служить: движение динамического объекта, технологический процесс, процесс организации вы пуска или продажи продукции. Дискретность многошагового процесса может быть естественной, связанной со сменой физического состояния объекта и принудительной, когда разбиение на этапы производится для организации процедуры решения задачи оптимизации. Для реализации движения на каждом шаге принимается решение либо в виде величины управления
где
На основании введенных понятий формулировка принципа оптимальности Беллмана, данная самим автором, имеет следующий вид: оптимальная стратегия обладает тем свойством, что, каково бы ни сало первоначальное состояние и решение в начальный момент, последующие решения должны составлять оптимальную стратегию относительно со стояния, полученного в результате первого решения. Для пояснения сформулированного принципа рассмотрим оптимальную траекторию в Из выше приведенной формулировки следует, что принцип оптимальности Беллмана дает достаточно общее необходимое условие оптимальности, которое можно применять как для непрерывных, так и для дискретных систем. Несмотря на кажущуюся простоту этого принципа, из него можно вывести совсем нетривиальные необходимые условия оптимальности траектории.
|
||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 721; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.126.69 (0.006 с.) |

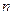 переменными состояния. Обозначим переменные состояния вектором
переменными состояния. Обозначим переменные состояния вектором  . Движение системы представляет собой многошаговый процесс, в котором последовательность состояний может быть задана:
. Движение системы представляет собой многошаговый процесс, в котором последовательность состояний может быть задана: - разностным уравнением
- разностным уравнением 
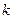 - индекс времени или шага,
- индекс времени или шага,  - управляющее воздействие;
- управляющее воздействие;
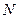 - число участков многошагового процесса,
- число участков многошагового процесса, - функция стоимости на каждом шаге.
- функция стоимости на каждом шаге. обозначим через
обозначим через  Эта точка делит траекторию на две части, принцип оптимальности утверждает, что отрезок оптимальной траектории от точки
Эта точка делит траекторию на две части, принцип оптимальности утверждает, что отрезок оптимальной траектории от точки 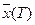 также является оптимальной траекторией независимо от предыстории системы, т.е. от того, каким образом система достигла состояния
также является оптимальной траекторией независимо от предыстории системы, т.е. от того, каким образом система достигла состояния  равно сумме его значений, вычисленных по двум отрезкам траектории. Отсюда следует, что можно построить траекторию, которая будет лучше исходной. Для этого надо выбрать вектор допустимого управления так, чтобы начальный участок траектории остался прежним, а ее второй участок совпал с штриховой кривой. Следовательно, мы пришли к противоречию с гипотезой оптимальности первоначальной траектории, и это означает, что нельзя улучшить второй участок траектории, т.е. этот отрезок оптимальной траектории в свою очередь также является оптимальным. Второй участок оптимальной траектории также является оптимальной траекторией и оптимальная стратегия не зависит от предыстории системы,- а определяется начальным условием и конечной целью. Если разделить траекторию на несколько отрезков и двигаться от конца (в обратном направлении), то можно последовательно доказать оптимальность всех отрезков, пользуясь принципом Беллмана и всякий раз рассматривая отрезок, прилегающий к последнему. Таким образом, оптимальность отдельных участков траектории определяется оптимальностью всей траектории. Обратное утверждение не имеет места, т.е. оптимальность всей траектории не следует из оптимальности отдельных участков.
равно сумме его значений, вычисленных по двум отрезкам траектории. Отсюда следует, что можно построить траекторию, которая будет лучше исходной. Для этого надо выбрать вектор допустимого управления так, чтобы начальный участок траектории остался прежним, а ее второй участок совпал с штриховой кривой. Следовательно, мы пришли к противоречию с гипотезой оптимальности первоначальной траектории, и это означает, что нельзя улучшить второй участок траектории, т.е. этот отрезок оптимальной траектории в свою очередь также является оптимальным. Второй участок оптимальной траектории также является оптимальной траекторией и оптимальная стратегия не зависит от предыстории системы,- а определяется начальным условием и конечной целью. Если разделить траекторию на несколько отрезков и двигаться от конца (в обратном направлении), то можно последовательно доказать оптимальность всех отрезков, пользуясь принципом Беллмана и всякий раз рассматривая отрезок, прилегающий к последнему. Таким образом, оптимальность отдельных участков траектории определяется оптимальностью всей траектории. Обратное утверждение не имеет места, т.е. оптимальность всей траектории не следует из оптимальности отдельных участков.


